大跨徑懸索橋動力特性分析

徐建華

（新疆維吾爾自治區交通規劃勘察設計研究院，新疆 烏魯木齊 830006）

0 引言

懸索橋是以懸索作為主要承重構件的橋梁，由主纜、索塔、錨碇、吊桿、橋面系等部分組成。懸索橋的主要承重構件是懸索，它主要承受拉力，其材料一般用抗拉強度高的鋼絲。懸索橋由于其構造簡單，受力明確[1]，同時可以充分利用材料的強度，并具有用料省、自重輕的特點，因此懸索橋與其他體系橋梁結構相比其跨越能力最大，多見于大跨徑橋梁。由于懸索橋跨徑大、整體剛度低，車輛和風荷載等動荷載作用明顯，因此對其進行動力特性分析，掌握其動力特性是非常必要的。通常可采用解析法和有限元法對懸索橋的動力特性進行計算。本文采用有限元方法，利用功能強大的有限元分析軟件ANSYS對一大跨懸索橋的動力特性進行了分析，得到了有價值的結果。

1 有限元法

有限元法是目前在結構分析中應用最廣泛的方法，下面對有限元的求解過程作一簡要介紹[2]：

1.1 結構的離散化

將所需要分析的結構物分割為具有不同大小和形狀的單元個體，彼此之間相互相連，使其成為一個有限單元體的集合。顯然單元越小對結構物的近似程度也就更加好，其計算結果也就會更加精確，然而其同樣會帶來計算量和誤差的增大。為了準確有效的模擬結構物，需要確定所采用的分割單元的形狀、大小及其數目等問題。

1.2 選擇位移模式

通常需要確定一組變量，用這組變量可以表示結構物離散化各個單元的位移、應力及其應變。通常選擇單元節點的位移來表示單元的位移、應力及其應變，因此選擇合適的位移函數就顯得尤為重要。由于進行數學運算時的方便性和模擬的準確性，通常情況下一般選擇多項式作為位移函數來進行有限元計算。根據選擇的位移函數，可以由結點位移得到單元內任一點的位移、應力及其應變，具體表達式如式（1）、式（2）、式（3）：

式中，u是單元內任一點的位移向量；δe為單元的結點位移向量；N稱為形函數矩陣，它的元素是位置坐標的函數。

1.3 單元特性分析

在選擇了合適的位移函數之后，可以根據能量原理、虛位移原理等方法來得到單元的相關特性。

1.4 整個結構平衡方程的建立

將根據第4步得到的結構每個單元特性進行集合就可得到結構的整體平衡方程。這個平衡方程仍然表示力與位移的關系，如式（4）所示：

式中，K為結構的整體剛度矩陣，由各個單元的單元剛度矩陣集合而成，通常采用直接剛度法來得到整體剛度矩陣；f為結構的荷載向量，由各個單元所受的等效節點力集合而成；δ為結構的結點位移矩陣。

1.5 聯立方程組求解結點位移和單元內力或應力

結合結構的邊界條件，對式（4）進行求解就可得到結構的結點位移，由得到的結點位移利用式1～3就能單元的位移、應力和應變。

2 有限元模型建立及初始平衡狀態確定

2.1 工程概況

本橋是橋型為三跨鋼筋混凝土懸索橋，其橋跨布置為50m+130m+50m，橋梁全長210m，其主纜的垂跨比，加勁梁為鋼筋混凝土桁架，索塔為H索塔，高為50m，基礎采用明挖擴大基礎。錨錠采用埋置式混凝土重力錨體，矩形擴大基礎。本橋主纜和吊索的材料均采用直徑為5.20mm的鍍鋅高強鋼絲。

2.2 有限元模型的建立

本文利用大型有限元通用軟件ANSYS采用有限元方法對懸索橋的動力特性進行求解，并建立了該懸索橋的有限元模型。全橋共1277個節點，3683個單元。其中主纜和吊索采用LINK10單元模擬，橋面板采用shell 63單元模擬，加勁梁采用beam4空間梁單元模擬。其邊界條件為在：索塔底部位置采用固結，主纜在錨固點處約束其三個線位移方向的自由度，在索塔頂部位置的索鞍采用耦合自由度的方式實現。該懸索橋的有限元模型見圖1。

圖1 懸索橋有限元模型

2.3 初始狀態的確定

由于在懸索橋的荷載作用中，其恒載所占的比例往往較大，同時由于懸索橋在恒載作用下會產生初應力而對結構的剛度有提高[3]。因此為了更準確的對懸索橋進行動力特性分析，就需要首先確定該懸索橋在恒載作用下初始平衡狀態。

本文首先假設懸索橋主纜為拋物線形狀，然后通過設置主纜跨中位置坐標為收斂條件采用迭代計算得到了懸索橋的初始平衡狀態。經過迭代計算后主纜跨中位置的標高與設計標高的差值為0.001302m，可以認為此時該模型能夠反映該懸索橋在恒載作用下的實際情況，可以該狀態為懸索橋的初始平衡狀態，用于該懸索橋的動力特性計算。

3 懸索橋動力特性分析

大跨徑懸索橋的動力特性與橋梁在風荷載、地震荷載及車橋耦合作用等動力荷載作用下結構的響應有著密切的聯系。對大跨徑懸索橋進行動力特性分析是對其進行動力荷載作用下結構分析的基礎。本文采用上文建立的有限元模型和懸索橋的初始平衡狀態為基礎對該懸索橋進行了準確的動力特性分析。其前10階的自振頻率值和振型描述見表1。

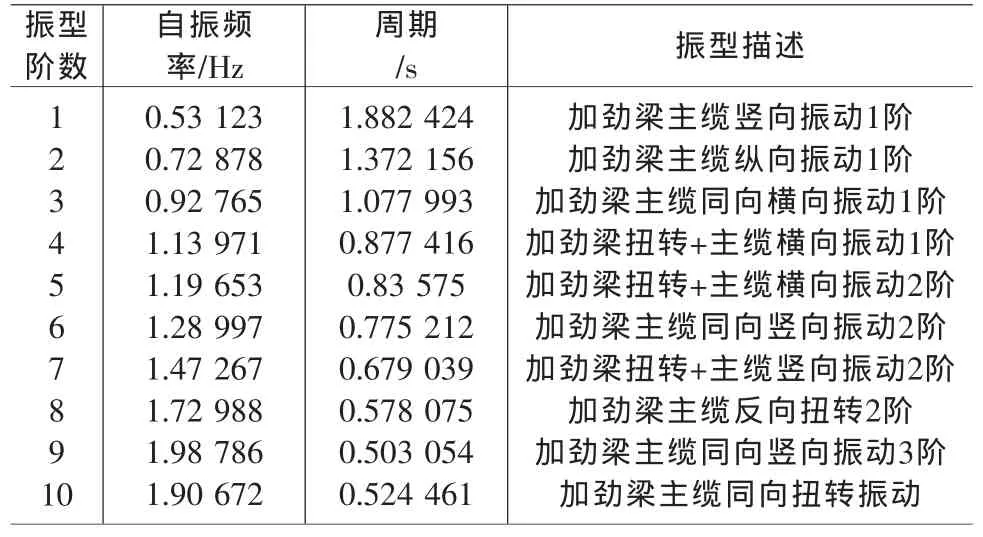
表1 懸索橋前10階自振頻率及其振型描述

由表1所示的計算結果可知，由于懸索橋的整體剛度較小，所以與拱橋、連續剛構橋、斜拉橋等橋型相比懸索橋的基頻較小，懸索橋屬于長周期振型結構。該懸索橋的第1階自振頻率為0.53123Hz，振型為加勁梁主纜豎向振動1階。其低階振型主要表現于加勁梁和主纜的振動。

該懸索橋的前3階振型為懸索橋三個方向的振動，懸索橋的跨徑較大，同時其加勁梁的剛度較小，所以在第4階振型就出現了加勁梁的扭轉。為了增加加勁梁的抗風能力，有必要對加勁梁進行抗風設計和考慮車橋耦合振動影響以及風—車—橋三者的耦合振動。

4 結語

大跨徑懸索橋動力特性與其在動力荷載作用下的響應密切相關。本文利用結構分析軟件ANSYS對某大跨懸索橋進行了動力特性分析計算，得到了大橋的各階自振頻率和振型。懸索橋的跨徑較大，同時其加勁梁的剛度較小，所以要特別注意加勁梁的抗風設計、車橋耦合振動影響以及風—車—橋三者的耦合振動。

[1]顧安邦.橋梁工程[M].北京：人民交通出版社，2000.

[2]徐榮橋.結構分析的有限元法與MATLAB程序設計[M].北京：人民交通出版社，2006.

[3]陳仁福.大跨懸索橋理論[M].成都：西南交通大學出版社，1994.