等效靜力風荷載背景和共振之間的耦合效應

柯世堂，王法武，周 奇，周志勇，趙 林

（1.南京航空航天大學 土木工程系，南京 210016；2.汕頭大學 風洞實驗室，廣東 汕頭 515063；3.同濟大學 土木工程防災國家重點實驗室，上海 200092）

在求解大跨度屋蓋結構的風致響應和等效靜風荷載（ESWLs）時，可以根據結構的動力特性和風荷載的自身特征，將響應分成背景和共振兩個分量求解，然后采用一定的組合方法來獲得總風致響應。該思路要求在求解時考慮背景與共振、共振與共振、背景與背景之間的三層耦合項，傳統的基于荷載響應相關方法［1］（LRC）和慣性風荷載方法［2］（IWL）的三分量方法無法精確求解這三層耦合項。很多學者對此進行了研究，并提出了有效的改進方法，例如Holmes等［2－3］和Irwin［4］最早提出了背景和共振分量的計算方法；Zhou等［5］、Chen等［6］和 Zhang［7］將這一方法進一步發展，明確了三分量方法的求解思路；隨后針對共振分量求解中的耦合效應問題，周晅毅等［8］、顧明等［9］、陳波等［10］、謝壯寧等［11］、余世策等［12］、梁樞果等［13］和柯世堂等［14］對三分量方法 進行了不同的改進，其中顧明等在中國最早采用三分量方法對上海金茂大夏、上海鐵路南站等結構進行ESWLs分析，并對比陣風荷載因子法（GLF）結果認為三分量法的結果更加精確合理；陳波等提出的Ritz－POD方法可進行風振響應精細化分析；謝壯寧等基于LRC的完全二次型組合獲取結構的風振響應和ESWLs，不區分背景和共振分量。這些改進方法更好的解決了大跨屋蓋結構風致響應和ESWLs的兩層耦合項問題：1）共振模態的選擇及模態間的耦合項求解難題；2）采用準靜力方法求解背景分量以考慮所有模態對于背景響應的貢獻。對于背景與共振模態之間的耦合效應，缺乏簡單有效的計算方法，因此大多直接采用SRSS方法組合背景和共振分量來獲得總脈動風致響應，這一作法對于背景和共振模態有較好分離的結構（高層建筑、高聳結構等）誤差較小，然而對于某些大跨度空間柔性結構，這一耦合分量理論上是需要考慮的。

本文基于模態加速度法和荷載響應相關原理，推導出結構ESWLs的真實理論組合公式，首次定義耦合恢復力協方差矩陣參數，提出用于補償背景和共振模態間耦合項的一致耦合方法（CCM）來求解結構的ESWLs，該方法避開了復雜的相關系數求解過程，且思路清晰，作用機理明確。并以某大跨度屋蓋結構為例，采用一致耦合方法進行風致響應和ESWLs計算，通過與全模態CQC計算結果進行對比分析，深入揭示了該結構風致響應中背景和共振耦合分量的參與機理，驗證了本文方法的高精度和有效性，并為此類結構風致響應和ESWLs的精確求解和機理研究提供新的思路。

1 背景和共振耦合項的理論推導

1.1 CCM方法的提出

柔性結構在風荷載激勵下的隨機動力響應方程可表達為：

式中：｛p（t）｝代表外部風荷載激勵向量；M、C、K 為結構的質量、阻尼和剛度矩陣（t）（t）、y（t）分別為節點的加速度、速度和位移向量。

使用模態疊加原理，式（1）可表達成

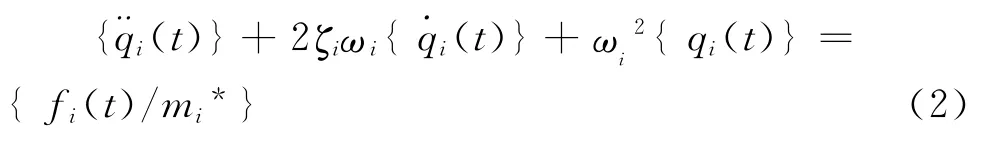
式中：qi（t）表示第i階模態的廣義位移向量；fi（t）表示第i階模態的廣義力向量。

對于柔性結構的風致動力響應來說，高階模態共振響應通常可以忽略，這樣動態位移可以表示為

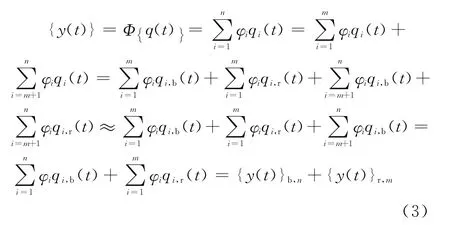
式中：Φ 為振型矩陣；φi為第i階振型向量；qi，b（t）為僅包含準靜力貢獻的第i階背景位移響應向量；qi，r（t）為僅包含共振效應貢獻的第i階共振位移響應向量；｛y（t）｝b，n為包含所有模態準靜力貢獻的背景響應向量；｛y（t）｝r，m為僅包含共振效應貢獻的前m階模態共振位移響應向量。

通常有2種頻域求解方法來計算式（3）中總的脈動風響應向量的均方差：

1）采用SRSS方法來組合背景和共振分量，可以表達為

式中：σt、σb，n、σr，m分別代表了響應向量｛y（t）｝、｛y（t）｝b，n、｛y（t）｝r，m的均方差。

其中背景分量可以作為準靜力響應，采用LRC方法來求解，共振分量采用慣性風荷載方法來計算。這一方法不能考慮背景和共振之間的模態耦合項，也不能很好的考慮共振模態之間的耦合項。

2）求解總脈動響應的組合方法為

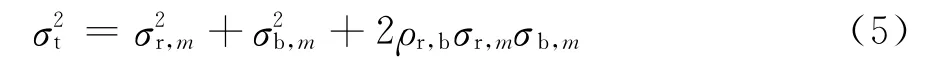
背景分量σb，m是前m 階背景位移向量｛y（t）｝b，m的均方差；ρr，b為背景分量和共振分量之間的相關系數，可以用下式計算

從式（5）中可以發現，背景分量僅僅包含前m階模態準靜力貢獻，相應地，背景和共振分量之間的交叉項也是僅僅包含前m階模態的貢獻。

基于SRSS組合的三分量法不能考慮背景和共振之間的交叉項，這對于相關系數ρr，b很小的結構是可以接受的，然后由于式（6）計算過程的復雜，并且沒有發展交叉項響應的ESWLs計算理論，因此在大多數的柔性結構風致響應和ESWLs計算中都不去考慮，其對于某些強耦合結構是不合理。

根據式（3）可以將脈動風總響應均方差精確的表達為

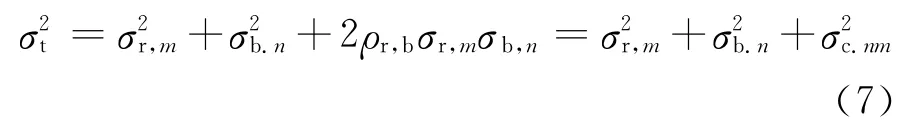
式中：σc，nm代表前n階背景分量和前m 階共振分量的交叉項。

和傳統方法最大不同在于式（7）能考慮所有模態的準靜力貢獻，前m階共振模態之間的耦合效應，n階背景模態和前m階共振模態之間的交叉項。

我們知道背景分量可以基于外荷載激勵的協方差矩陣，并采用LRC原理進行求解。借鑒這一思路，首次提出廣義恢復力協方差矩陣、共振恢復力協方差矩陣和耦合恢復力協方差矩陣這一概念，統一引入LRC方法來求解共振和交叉項分量，進而使得相應的ESWLs的求解有了理論基礎。這樣，式（7）變成：

式中 ［Cpp］t為廣義恢復力協方差矩陣；［Cpp］b為外荷載協方差矩陣；［Cpp］r共振恢復力協方差矩陣；［Cpp］c為耦合恢復力協方差矩陣；I為影響線矩陣。

這樣可以進一步變化耦合恢復力協方差矩陣的表達式為

這樣我們可以分別求解背景、共振和耦合恢復力協方差矩陣，在基于LRC方法獲得各響應分量和ESWLs分量。下面以共振分量為例，給出了其風振響應和等效靜風荷載各分量的推導過程。

1.2 背景、共振和耦合項恢復力協方差矩陣的推導

僅包含共振分量的第i階廣義模態響應為

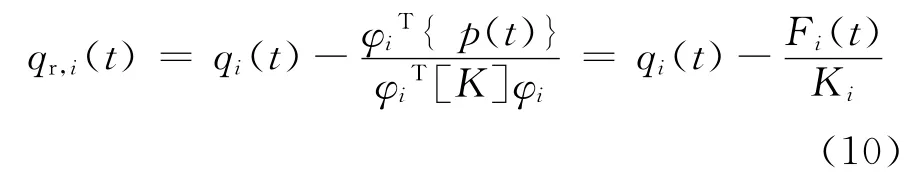
則第i階和第j階廣義共振模態響應的互功率譜為

從式（11）中可以發現，廣義共振模態響應的求解關鍵是確定廣義共振頻響傳遞函數。

綜合以上各式，廣義共振模態響應協方差矩陣可表示為

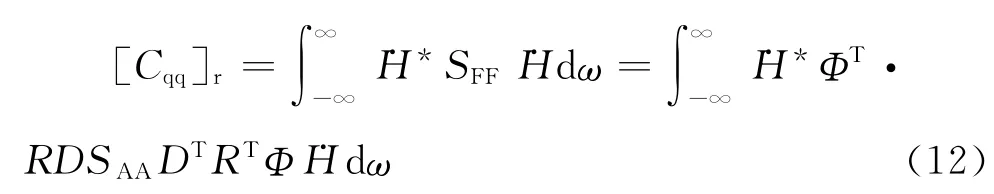
式中SAA為經POD［15］分解獲得的前s階時間坐標函數A（t）互功率譜矩陣，用作降階處理。

應用模態展開理論，結構僅包含共振分量的彈性恢復力可表示為

結合式（12）、（13），得到 ｛Peqq｝r的互協方差矩陣 ［Cpp］r為

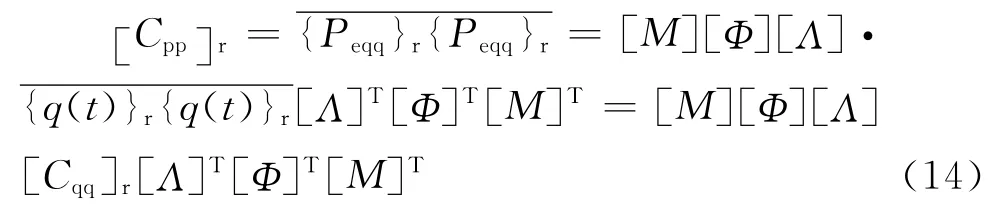
從以上的推導容易看出，｛Peqq｝r是僅包含共振分量的彈性恢復力向量，其精確程度取決于計算｛q（t）｝r時所取的模態階數和系統的動力特性；同理，把式（14）中求解 ［Cqq］r所需的共振頻響函數換成廣義頻響函數矩陣H即可得到總彈性恢復力協方差矩陣［Cpp］t；在通過風洞試驗獲得風荷載時程直接獲取背景恢復力協方差矩陣 ［Cpp］r；由式（8）定義的耦合彈性恢復力協方差矩陣 ［Cpp］c，其計算公式為

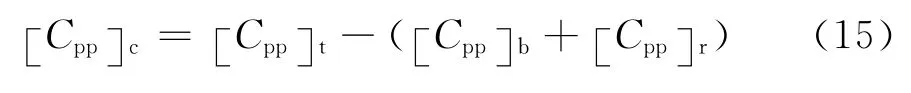
1.3 背景、共振及背景和共振耦合項各分量的求解

至此，求解共振、背景、耦合響應及其等效靜風荷載都可以轉化為求系統在相應恢復力作用的準靜力響應，進而可以利用LRC原理來計算。以共振分量為例給出求解過程

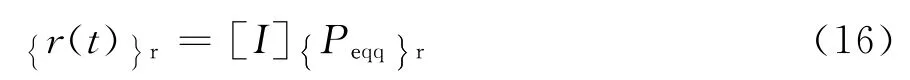
當I為柔度矩陣時，r（t）即為結構的共振響應，其響應的協方差矩陣為

則結構的共振響應為

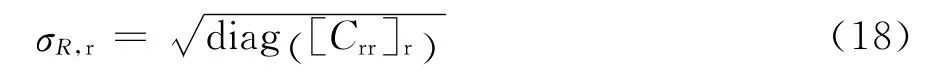
式中，diag（·）表示取矩陣的對角元素組成列向量。

響應Ri的對應的共振等效靜風荷載為

綜上可知，采用這一思路可以求解背景和共振耦合分量的風致響應和等效靜風荷載，只需將式（17）和（19）中的 ［Cpp］r換成 ［Cpp］c。需要注意的一點是，由式（17）求解的耦合響應協方差矩陣中的元素可能會出現負數的情況，分析其原因：元素為正時說明忽略耦合分量會低估結構的響應，為負時說明忽略耦合分量會高估結構的響應。在代入到公式（18）求解耦合響應時一律按正值代入，但在組合時必須要考慮其正負影響。

1.4 總風致響應和ESWL的組合

最后組合脈動風總響應

式中σr、σb和σc分別為共振、背景和耦合響應分量，應該注意的是對于耦合分量的組合，一定要考慮其正負影響。

采用線性組合方式組合各分量得到總的等效靜力風荷載，這樣可以保證總的等效靜力風荷載是真實的荷載分布形式，并且在該荷載作用下，能確保控制點和非控制點的響應都與峰值響應一致。

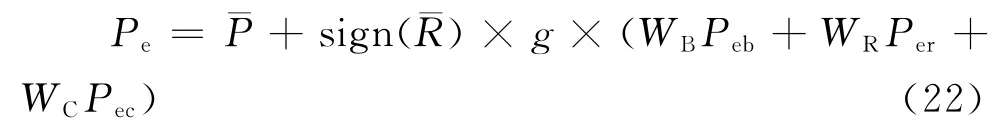
式中：Peb、Pec為等效靜力風荷載背景和耦合分量；WB、WR、WC分別為Per、Peb和Pec的權值系數。

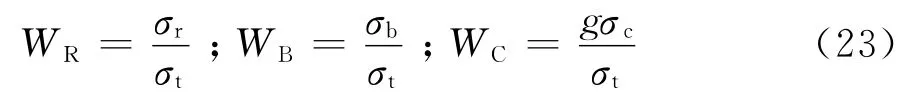
下面驗證由總等效靜力風荷載引起的靜力響應的有效性：

推導可知本文方法計算的結構風振響應結果正確，則其等效靜風荷載一定準確無誤。

2 算例分析

某大跨度屋蓋結構形式新穎（見圖1），全長228m，寬90m，屋頂結構采用斜放四角錐鋼網架結構，整個雙向曲面屋頂由6根“蘑菇柱”支撐，“蘑菇柱”均勻分布，很好的分散屋頂傳來的荷載。圖1中標出的A～F6個節點是該結構上具有代表性的典型節點，文中的分析均以這6個節點的響應特征為例。

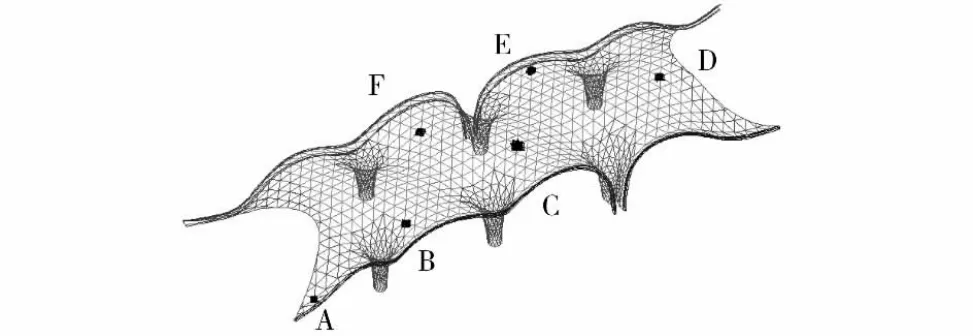
圖1 博物館計算模型及典型節點示意圖

圖2給出了結構前300階自振頻率的分布情況，可以看出結構的自振頻率較低，在1.5～13Hz頻率之間存在300階頻率，特別在10～13Hz之間分布了200階頻率，其分布十分密集。計算時取10m高的基本風速為60m／s，阻尼比為0.02，峰值因子統一采用3.5。

圖2 結構固有頻率分布圖

圖3給出了典型節點E的位移響應功率譜密度函數圖，從圖中可以看出，該節點的風振響應中第1階模態貢獻的能量很小，主要是由5、9、17和30階模態貢獻能量，且準靜力效應貢獻的背景分量不可忽略，但從響應功率譜圖中無法直接觀察背景和共振之間的交叉項所占比重的影響，需要進一步分析。

圖3 節點A位移響應功率譜圖

采用本文提出的CCM方法、改進的三分量方法（即考慮了共振模態之間的耦合效應）以及基于全模態CQC方法對結構進行頻域計算，提取這6個典型節點的響應根方差。表1給出了這3種方法計算的響應結果，可以發現：1）對于博物館這類大跨空間結構，必須考慮多階模態的貢獻，對每個結構應具體分析后確定參振模態數目，通過逐漸增加計算模態數并和全模態CQC法的計算結果（即為精確解）對比確定該博物館結構風振分析采用100階即可；2）采用改進的三分量方法的計算結果對于博物館結構的脈動風致響應來說誤差較大，其中E點的誤差最大，達到了－14.6%，說明忽略背景和共振模態之間的耦合分量對于該結構來說有時偏于危險，需要引起重視；3）本文的CCM法計算結果和全模態CQC計算的精確解的結果吻合的較好，最大的誤差在F點，僅為1.94%，絕對平均誤差連1%都不到，說明本文方法具有較高的精度。

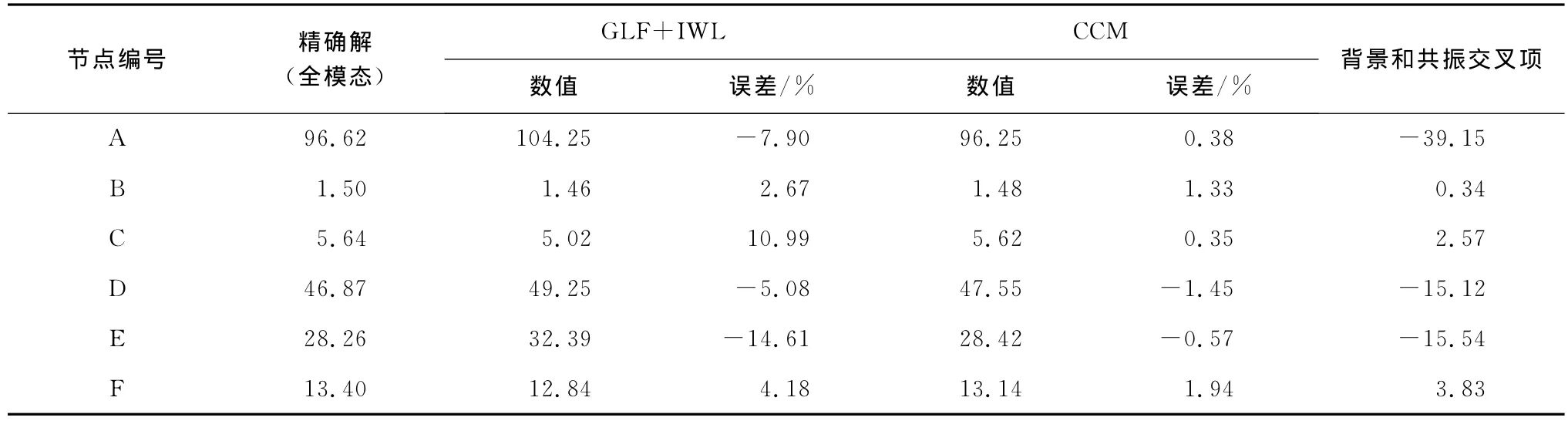
表1 典型節點脈動風致響應根方差 mm

為了研究獲得的等效風荷載的精度及有效性，分別給出本文方法和GLF＋IWL的三分量法所得到的等效靜風荷載結果與在此等效靜風荷載作用下的結構響應結果。從圖4、5中可以看出，采用本文方法所得到的等效靜風荷載結果略小于三分量的結果，但應用這兩種方法所得到的結構等效靜風響應結果在控制點上的結果是完全一致的。不僅如此，通過與精確解的比較表明：本文方法在保證控制點等效的同時，還保證了結構其他部位的響應更接近于實際可能發生的最不利響應，而傳統的三分量方法卻無法做到這一點。進一步說明對于某些大跨度屋蓋結構來說，背景和共振交叉項的貢獻不能忽略。

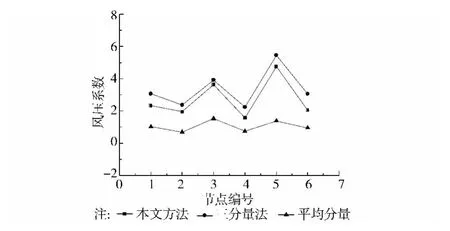
圖4 等效靜風荷載計算結果

圖5 等效靜風響應計算結果

3 結語

系統地討論了大跨度屋蓋結構等效靜風荷載研究的關鍵問題，即如何解決共振模態之間的耦合效應、背景和共振模態之間的耦合效應問題。從隨機振動理論出發，推導出用于補償共振與背景間耦合分量的一致耦合法。并將其用于某大型博物館結構的風致響應及等效靜風荷載分析，驗證了CCM法相比傳統的三分量方法可以更加精確的求解結構的背景、共振及交叉項響應，并賦予等效靜風荷載以更明確的物理意義。分析結果表明對于某些大跨度屋蓋結構，不僅要考慮各共振模態之間的耦合效應，背景和共振之間耦合效應同樣不能忽略，而本文的CCM方法可以很好的解決這一問題。

［1］Davenport A G.Gust loading factor［J］.Journal of the Structural Division，1967，93（ST3）：11－34.

［2］Holmes J D.Wind loading of parallel free－standing walls on bridges，cliffs，embankments and ridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89（14）：1397－1407.

［3］Holmes J D，Kasperski M.Effective distributions of fluctuating and dynamic wind loads［J］.Transactions of the Institution of Engineers， Australia， Civil Engineering，1996，38：83－88.

［4］Irwin P A.The role of wind tunnel modeling in the prediction of wind effects on bridges［C］／／Bridge aerodynamics，Balkema，Rotterdam，The Netherlands，1998：59－85.

［5］Zhou Y，Kareem A，Gu M.Equivalent static buffeting laods on structures ［J］. Journal of Structural Engineering，2000，126（8）：989－992.

［6］Chen X，Matsumoto M，Kareem A.Aerodynamic coupling effects on flutter and buffeting of bridges［J］.Journal of Engineering Mechanics，2000，126（1）：17－26.

［7］張相庭.國內外風荷載規范的評估和展望［J］.同濟大學學報，2002，30（5）：539－543.Zhang X T.Evaluation and prospect for wind loading codes at home and abroad ［J］.Journal of Tongji University，2002，30（5）：539－543..

［8］周晅毅，顧明.上海鐵路南站屋蓋結構風致抖振響應參數分析［J］.同濟大學學報，2006，34（5）574－579.Zhou X Y，Gu M.Parametric analysis of wind－induced buffeting responses of roof structure of Shanghai south railway station ［J］.Journal of Tongji University，2006，34（5）574－579.

［9］顧明，周晅毅，黃鵬.大跨屋蓋結構風致抖振響應研究［J］.土木工程學報，2006，39（11）：37－42.Gu M，Zhou X Y.A study on the wind－induced buffeting responses of large－span roof structures ［J］.Journal of Civil Engineering，2006，39（11）：37－42.

［10］陳波，武岳，沈世釗.大跨度屋蓋結構等效靜力風荷載中共振分量的確定方法研究［J］.工程力學，2007，24（1）：51－55，66.Chen B，Wu Y，Shen S Z.Study of the resonant component of equivalent static wind loads on large span roofs［J］.Engineering Mechanics，2007，24（1）：51－55，66.

［11］謝壯寧，倪振華，石碧青.大跨度屋蓋結構的等效靜風荷載［J］.建筑結構學報，2007，28（1）：113－118.Xie Z N，Ni Z H，Shi B Q.Equivalent static wind loads on large span roof structures［J］.Journal of Building Structures，2007，28（1）：113－118.

［12］余世策，樓文娟，孫炳楠.開孔結構屋蓋風致響應的模態分析法［J］.應用力學學報，2009，26（1）：76－81.Yu S C，Lou W J，Sun B N.Modal analysis to windinduced response for roof structures with wall opening［J］.Journal of Applied Mechanics，2009，26（1）：76－81.

［13］梁樞果，吳海洋，郭必武，等.大跨度屋蓋結構等效靜力風荷載數值計算方法［J］.華中科技大學學報，2008，36（4）：110－114.Liang S G，Wu H Y，Guo B W，et al.Numerical calculation of evaluating equivalent static wind loads on long span roof structures［J］.Journal of HUST，2008，36（4）：110－114.

［14］柯世堂，葛耀君，趙林，等.大型冷卻塔結構的等效靜力風荷載［J］.同濟大學學報，2011.8，39（8），1132－1137.Ke S T，Ge Y J，Zhao L，et al.Equivalent static wind loadings of large cooling towers［J］.Journal of Tongji University，2011，39（8）：1132－1137.

［15］Ke S T，Ge Y J，Zhao L，et al.A new methodology for analysis of equivalent static wind loads on super－large cooling towers ［J］.Journal of Wind Engineering ＆Industrial Aerodynamics，2012，111（3）：30－39.