考慮剪脹和軟化的巷道圍巖彈塑性分析

魏建軍

（1.中國礦業大學 深部巖土力學與地下工程國家重點實驗室，江蘇 徐州， 221008；2.江蘇建筑職業技術學院 江蘇省建筑安全與減災工程研發中心，江蘇 徐州， 221116）

隨著礦山開采的大規模進行和采深的增加，造成的災害日益增多，對深部資源的安全高效開采造成巨大威脅。深部巖體處于高地應力、高溫、高滲透壓的惡劣環境中，使得巖體的組織結構、力學性態和工程響應均發生根本性變化，圍巖表現出特殊的非線性力學行為［1－3］。深部巷道開挖后二次應力場形成引起的高地應力集中導致圍巖壓剪應力超過其強度進而破壞處于剪脹狀態；同時，開挖后的近表圍巖內空隙水壓力降低引起的圍巖有效應力增大加劇了圍巖的破裂；高地溫帶來的附加應力對圍巖破裂擴展帶了不可忽視的影響。巖石進入峰后階段由于應力跌落方式的不確定性，難以用經典理論來描述［4－5］。Hoek等［6］于 1997年提出了估算巖石峰后力學行為的方法，給出了巖石峰后力學模型。隨后，學者對圍巖的彈塑性分析進行了大量研究。其他國家的研究集中于基于Hoek－Brown強度準則采用彈脆塑性模型進行分析［7－10］，中國的研究則考慮巖石的非線性軟化和破壞過程，但在解析計算方面為了求解方便往往設置不合理的限制，如在圍巖破壞過程中體應變設置為零［11－12］、彈性模量設為常數［13］等，這些方法均不符合巷道受擾變形的機制。

圓形硐室的軸對稱彈塑性分析是個經典問題，有許多學者進行過研究。文獻［8］對 Mohr－Coulomb介質中的應變軟化過程進行了研究，其中考慮了黏結力和剪脹角的下降，內摩擦角在軟化變形中保持不變；文獻［7］將圓形硐室圍巖內形成的塑性區劃分為一系列的同心圓環，采用差分法求解得到軟化區與殘余強度區尺寸以及相應的位移分布；文獻［14－16］考慮了統一強度理論，軟化段采用雙折線模型，得到了硐室圍巖彈塑性分析的統一解。

本文根據巖土體材料在出現應力跌落以前或多或少要經過一段塑性變形的過程，考慮引入應力跌落條件閾值來判斷是否出現應力跌落，構建一個彈塑脆性模型，考慮圍巖的應變軟化和剪脹特性，采用Mohr－Coulomb屈服準則對圓形硐室圍巖進行彈塑性分析。

1 彈塑脆性模型及問題描述

前人所采用的應力跌落模型的應力 應變曲線由兩段組成，即屈服前的線彈性階段和屈服后的殘余強度階段，即認為材料在達到彈性極限之前為線彈性，一旦達到彈性極限，便會屈服，并且強度降為殘余強度。其實，真正彈脆性材料是不存在的，材料在出現應力跌落以前，或多或少要經過一段塑性變形的過程。因此，本文采用彈塑脆性模型，如圖1所示。巷道圍巖應力 應變曲線可分為處于彈性區、塑性發展區和殘余變形區3種狀態。

圖1 巖石的應力應變曲線

模型以微元體中與最大主應力和最小主應力都成45°的面上的最大剪應變來描述巖石不可逆的塑性變形，當最大剪應變達到某一值時，材料即出現脆性軟化，該最大剪應變的臨界值即為軟化閾值，其值在下文用γf表示。

本文研究巖土材料中平面應變條件下的圓孔問題。如圖2所示，在彈塑脆性材料的無限空間中作用有靜水壓力p0，其中有一無限長圓形硐室，開挖半徑為a；支護荷載為pi；隨著圍巖卸荷發展，硐室周圍巖土體進入塑性，貼近洞口部分區域剪應變達到軟化閾值，材料出現軟化形成環形軟化區，這樣巷道圍巖自內向外由軟化區、塑性區和彈性區3部分組成，為書寫方便，其對應的物理量分別附下標s、p、e以示區別。

圖2 圓形硐室圍巖彈塑性分析模型

2 基本假定與方程

做如下基本假定：

1）圍巖材料均勻、連續、各向同性。

2）材料屈服服從Mohr－Coulomb準則。

3）圍巖材料具有明顯的剪脹特性，塑性及軟化區體積應變不等于0。采用線性剪脹模型，位移以指向洞內為正，設剪脹參數為βi，則塑性應變與的關系為：

式中：ψi為剪脹角，一般小于或等于內摩擦角φ；i表征圍巖所處區域。

4）圍巖塑性軟化區的泊松比為常數，彈性模量僅在軟化區劣化，劣化系數k＝Es／Ee，取值范圍0～1，可以通過地質探測資料獲得。

在各區內圍巖應力滿足平衡方程：

巖石在出現塑性屈服和軟化時，其應力滿足Mohr－Coulomb準則，且認為圍巖被動承受地壓力，σθ＝σ1，σr＝σ3，在塑性區和軟化區內統一表示為：

式中N和S為材料參數。

式中：ci、φi為黏聚力和內摩擦角；i統一表示圍巖所處的不同區域。

應變公式為：

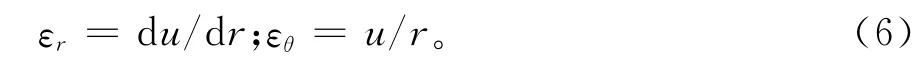
3 問題求解

3.1 軟化區分析

在軟化區（a≤r≤Rs）

式中：Ds＝Cscotφs。

由幾何方程（6）、廣義虎克定律及變形協調方程：?εθ／?r＝ （εr－εθ）／r可解出應變和位移表達式：

式中：ηs＝ （1－v）（Nsβs＋1）／（Ns＋βs）－v；βs為軟化區剪脹參數；k為彈模劣化系數；A為積分常數。

3.2 塑性區分析

在塑性區（Rs≤r≤Rp）和軟化區計算類似，可得塑性區的應力表達式為：

式中：ηp＝ （1－v）（Npβp＋1）／（Np＋βp）－v；B 為積分常數。

3.3 彈性區分析

在彈性區（Rp≤r＜∞）圍巖的應力和應變為：

將式（13）中的A 和B 代回式（8）、（10），可得軟化區、塑性區的應變和位移表達式。

3.4 巷道破壞半徑的確定

確定巷道圍巖破壞范圍通常采用邊界處應力或位移連續條件。本文在彈塑性交界處彈性應力滿足塑性屈服狀態，即：

將式（9）、式（11）的有關式帶入式（14）可得：

式（15）建立了塑性圈半徑和軟化區半徑的關系，尚需要再尋找一個條件方可確定其解。

圍巖的破壞除了滿足應力條件外還應滿足變形條件。在判定圍巖或地下結構穩定性時，常以洞周切向應變值來進行控制，即認為圍巖的最大剪應變達到或超過允許值時圍巖就破裂進入軟化松動區。考察理想塑性區與軟化區交界處塑性區一側的剪應變，可表示為：

式中γf為塑性區圍巖抗剪強度破壞時的應變值，對應于三軸試驗測得的巖樣相應的臨界剪應變值。

由塑性區應變表達式（10）代入上式整理后得到塑性區圍巖軟化破裂的變形條件。

將式（15）和（17）聯立即可獲得軟化區半徑Rs和塑性區半徑Rp。

4 算例與討論

采用文獻［17］的計算實例。貴州錦屏二級水電站大水溝廠房支1洞位于東雅礱江右岸，地質巖性主要為大理巖，截面尺寸為3.26m×3.30m（寬×高），近似為圓形硐室。經過地應力實測表明探洞斷面上豎直主應力約為22.9MPa，水平主應力約為19.8MPa。

結合現場測試與設計院試驗結果確定本研究段的巖體力學計算參數為：彈性模量Ee＝Ep＝16GPa，Es＝2GPa；泊松比υ＝0.3；在彈性區和塑性區粘聚力cp＝2.5MPa，摩擦角φp＝35°；在塑性軟化區粘聚力cs＝1.4MPa，摩擦角φ＝23°。取剪脹角ψp＝18°，ψs＝13°，巖石的應變軟化閾值分別取0.001、0.004、0.01。地應力近似為兩向等壓，取p0＝21MPa；支護荷載pi＝0。通過計算得到其對應的軟化區及塑性區范圍見表1。圍巖的應力與應變分布如圖3所示。

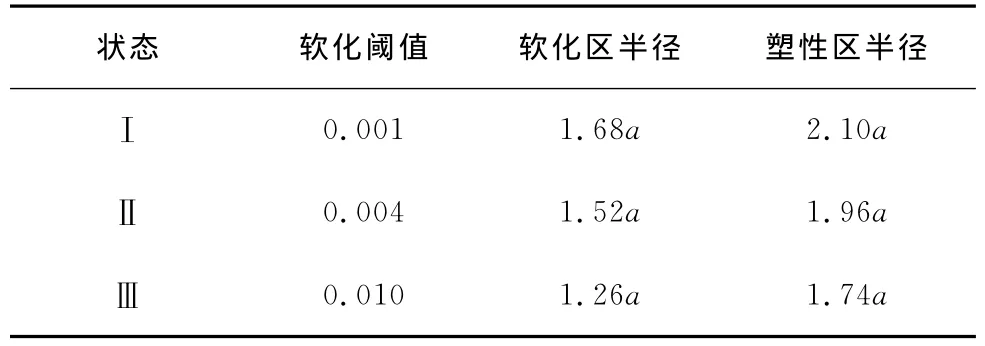
表1 塑性范圍計算結果

圖3 軟化閾值對圍巖應力與應變的影響

從圖3可以看出，軟化閾值對分析結果影響顯著，隨著軟化閾值減小，軟化區和塑性區范圍增大，在相同松動圈半徑位置，應力隨之減小，應變則增大。

圖4為軟化閾值取0.004時，圍巖彈模劣化系數k分別取0.125、0.300、0.600三種情況下的應變曲線。從結果可以看出，近巷圍巖彈模劣化是導致深部巷道圍巖變形較大的因素之一，不考慮圍巖彈模劣化計算結果偏危險。

圖4 彈模劣化系數k對圍巖應變的影響

5 結 論

1）在理想彈脆性模型的基礎上，加上一個軟化閾值，建立了彈塑脆性模型，研究巖土開挖中的硐室圍巖彈塑性問題，基于M－C強度理論和非關聯流動法則，得到了圓形硐室圍巖應力與變形解析表達式。

2）軟化閾值變化對圍巖應力場影響顯著，隨著軟化閾值的增大，塑性區圍巖應力增大，變形減小，反之亦然。

3）分析了巖石彈模劣化系數對圍巖變形的影響。隨著劣化程度的加大，破裂區范圍變化不大，圍巖變形顯著，是地下工程近巷圍巖大變形的重要原因。

［1］周宏偉，謝和平，左建平.深部高地應力下巖石力學行為研究進展［J］.力學進展，2005，35（1）：91－99.Zhou H W，Xie H P，Zuo J P.Developments in researches on mechanical behaviors of rocks under the condition of high ground pressure in the depths ［J］.Advances in Mechanics，2005，35（1）：91－99.

［2］王德榮，甄樹新，汪新紅，等.深部坑道圍巖壓力與變形分析［J］.巖土力學，2007，28（3）：70－77.Wang D R，Zhen S X，Wang X H，et al.Analysis of pressure and deformation of wall rock near deep tunnel［J］.Rock and Soil Mechanics，2007，28（3）：70－77.

［3］劉泉聲，盧興利.煤礦深部巷道破裂圍巖非線性大變形及支護對策研究［J］.巖土力學，2010，31（10）：3273－3280.Liu Q S，Lu X L.Research on nonlinear large deformation and support measures for broken surrounding rocks of deep coal mine roadway［J］.Rock and Soil Mechanics，2010，31（10）：3273－3280.

［4］張黎明，王在泉，李華峰，等.粉砂巖峰后破壞區應力脆性跌落的試驗和本構方程研究［J］.實驗力學，2008，23（3）：234－240.Zhang L M，Wang Z Q，Li H F，et al.Theoretical and experimental study on siltstone brittle stress drop in post failure region ［J］.Journal of Experimental Mechanics，2008，23（3）：234－240.

［5］王水林，王威，吳振君.巖土材料峰值后區強度參數演化與應力－應變曲線關系研究［J］.巖石力學與工程學報，2010，29（8）：1524－1529.Wang S L，Wang W，Wu Z J.Study of relationship between evolution of post－peak strength parameters and stress－strain curves of geomaterlals［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29（8）：1524－1529.

［6］Hoek E，Brown T E.Practical estimates of rock mass strength ［J］.International Journal of Rock Mechanics and Mining Sciences，1997，34（8）：1165－1186.

［7］Sharan K S.Eastic－brittle－plastic analysis of circular openings in Hoek－Brown media ［J］.International Journal of Rock Mechanics and Mining Sciences，2003，40（6）：817－824.

［8］Lee K Y，Pietruszczak S.A new numerical procedure for elasto－plastic analysis of a circular opening excavated in a strain－softening rock mass ［J］.Tunnelling and Underground Space Technology，2008，23（5）：588－599.

［9］Carranza T C，Fairhurst C.The elasto－plastic response of underground excavations in rock masses that satisfy the Hoek－Brown failure criterion ［J］.International Journal of Rock Mechanics and Mining Sciences，1999，36（6）：777－809.

［10］Chandra S，Nilsen B，Ming L.Predicting excavation methods and rock support：a case study from the Himalayan region of India［J］.Bulletin of Engineering Geology and the Environment，2009，69（2）：257－266.

［11］潘岳，王志強.基于應變非線性軟化的圓形硐室圍巖彈塑性分析［J］.巖石力學與工程學報，2005，24（6）：915－921.Pan Y， Wang Z Q.Elasto－plastic analysis on surrounding rock of circular chamber based on strainnonlinear softening ［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（6）：915－921.

［12］王亮，趙均海，李小偉.巖質圓形隧洞圍巖應力場彈塑性新解［J］.工程地質學報，2007，15（3）：424－428.Wang L，Zhao J H，Li X W.New elasto－plastic solution of rock circular tunnel surrounding rockmass stress field［J］.Journal of Engineering Geology，2007，15（3）：424－428.

［13］蔣斌松，張強，賀永年，等.深部圓形巷道破裂圍巖的彈塑性分析［J］.巖石力學與工程學報，2007，26（5）：983－986.Jiang B S，Zhang Q，He Y N，et al.Elastoplastic analysis of cracked surrounding rocks in deep circular openings［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（5）：983－986.

［14］范文，俞茂宏，陳立偉，等.考慮剪脹及軟化的洞室圍巖彈塑性分析的統一解［J］.巖石力學與工程學報，2004，23（19）：3213－3221.Fan W，Yu M H，Chen L W，et al.Unified elastoplastic solution for surrounding rocks of openings with consideration of material dilatancy and softening ［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（19）：3213－3221.

［15］李同錄，陳立偉，俞茂宏，等.考慮材料軟化的洞室圍巖彈塑性分析的統一解［J］.長安大學學報：自然科學版，2004，24（3）：49－52.Li T L，Chen L W，Yu M H，et al.Unified solution of elastic－plastic surrounding rocks of cavity considering material softening［J］.Journal of Chang'an University：Natural Science Edition，2004，24（3）：49－52.

［16］張常光，胡云世，趙均海，等.深埋圓形水工隧洞彈塑性應力和位移統一解［J］.巖土工程學報，2010，32（11）：1738－1746.Zhang C G，Hu Y S，Zhao J H，et al.Elastic－plastic unified solutions for stresses and displacements of a deep buried circular hydraulic tunnel ［J］.Chinese Journal of Geotechnical Engineering，2010，32（11）：1738－1746.

［17］江權.高地應力下硬巖彈脆塑性劣化本構模型與大型地下洞室群圍巖穩定性分析［D］.武漢：中國科學院武漢巖土力學研究所，2007.