煤礦用鉆裝機挖臂機構動力學仿真分析

唐 娟，楊 林，2

(1.中煤科工集團重慶研究院， 重慶 400039;2.瓦斯災害應急信息技術實驗室， 重慶 400039)

0 引言

隨著經濟的高速發展，煤礦安全高效生產越發重要。煤礦巷道用全液壓鉆裝機可以代替耙斗裝巖機和液壓臺車實現巖石巷道掘進除渣和鑿巖鉆孔作業，在提高生產效率的同時減少了安全隱患。鉆裝機主要是由扒渣工作裝置(挖臂)、鑿巖推進工作裝置(鉆臂)、刮板運輸機組成，其中挖臂是由水平擺動座、動臂、斗桿、四桿機構以及扒斗5個部分串聯而成(如圖1所示)，是鉆裝機中關鍵的工作部件，其作業效率決定了鉆裝機的裝載性能。

鉆裝機除渣作業依賴于挖臂各個部件之間的相對轉動。對挖臂進行動力學分析和建模是完成挖臂結構設計和實現挖臂運動控制所必需的。挖臂是由多個轉動關節串聯而成，是由多個剛體組成的動力學系統，具有非線性以及多輸入、多輸出的特點，各個部件之間存在著復雜的耦合關系。為了使挖臂完成預期的作業路徑，每個關節必須提供一定規律的驅動力矩。

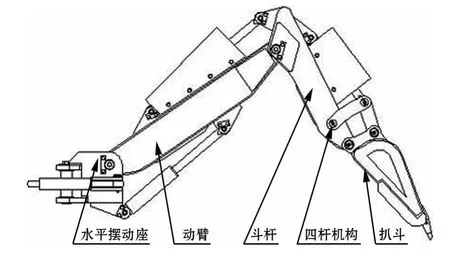
圖1 挖臂結構

通過建立挖臂機械手的動力學模型，并對機械手動力學模型進行分析與評價，可為得出合理的結構尺寸以及恰當的驅動油缸參數提供數據基礎。

1 挖臂作業軌跡空間

挖臂的作業空間范圍與挖臂上各個轉動部件的結構尺寸以及驅動油缸的參數有關，通過調整動臂、斗桿、扒斗以及四桿機構的結構尺寸以及相對應的驅動油缸參數(缸筒尺寸、缸桿尺寸、流量等)，可以得到不同的作業空間范圍。為了計算扒斗斗齒在基礎坐標空間內的活動范圍，在每個轉動部件上固結一個坐標系，然后描述這些坐標系之間的變換關系，通過這些變換關系，最終計算出斗齒的活動空間。為此，引入D－H(Denavit－Hartenberg)變換，利用一個4×4的齊次變換矩陣，表示兩個相鄰坐標系的變換關系，齊次變換矩陣可描述為下面的形式:

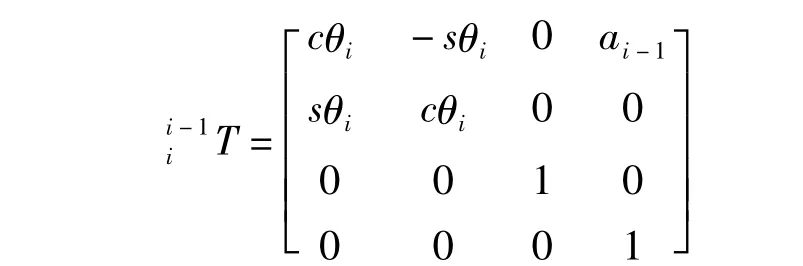
s——正弦函數 sin();

c——余弦函數 cos();

θi——兩個部件之間的關節角;

ai－1——兩部件關節間的長度，即相鄰坐標系原點間的距離。

齊次變換矩陣可以寫成如下形式:

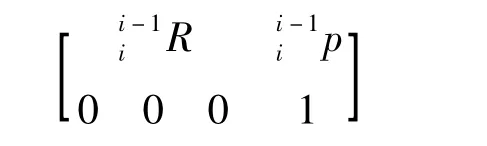
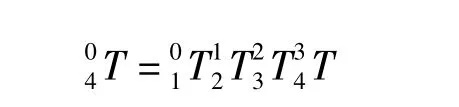
挖臂各個部件的參數如表1所示。

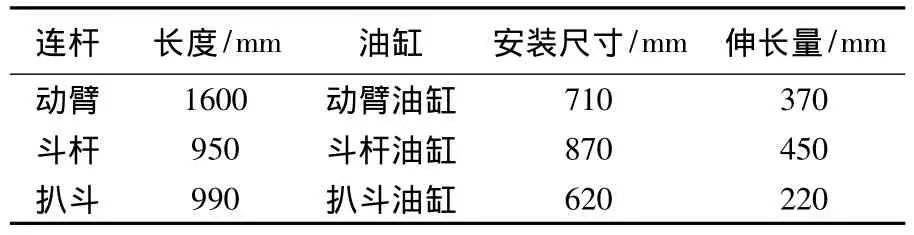
表1 構件參數表

利用上述公式，將斗齒尖所能達到的空間位置在Matlab軟件中描述出來，得到扒斗斗齒的作業空間包絡圖如圖2所示。

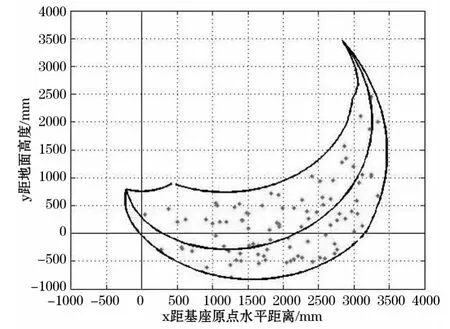
圖2 斗齒活動空間包絡圖

2 動力學分析

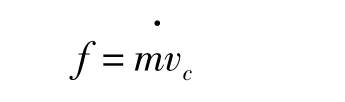
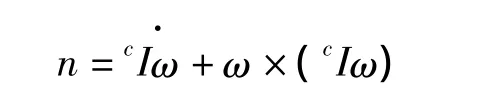
規定坐標系{c}的坐標原點為剛體的質心，相對于坐標系{c}，慣性張量cI定義為3×3的對稱矩陣:

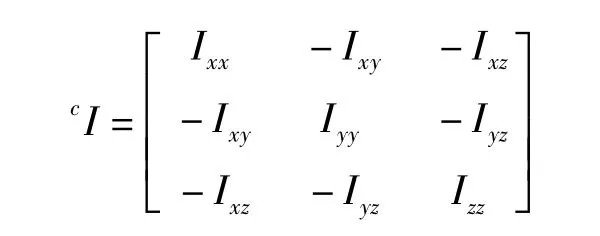
式中，對角線元素是剛體繞三坐標軸x，y，z的質量慣性矩:

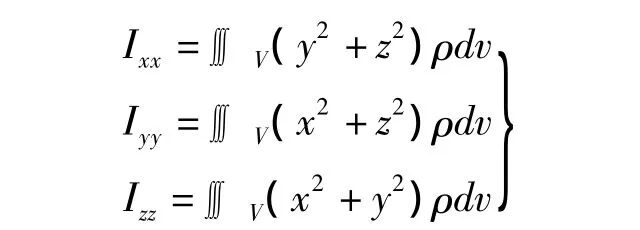
其余元素的慣性積:

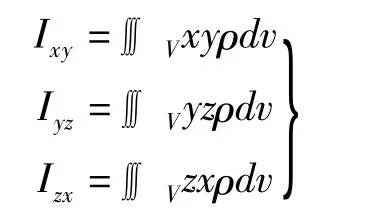
式中，ρ——結構件的密度;

挖臂斗齒的運動速度可以由兩部分組成:扒斗坐標系坐標原點的速度和加速度，以及扒斗相對于扒斗坐標系的角速度和角加速度。vi和ωi分別表示挖臂的各個部件坐標系{i}相對于基座坐標系{0}的速度，ivi和iωi則說明vi和ωi在本部件坐標系{i}中表示的線速度和角速度，同理i+1vi+1和i+1ωi+1表示在部件坐標系{i+1}中的線速度和角速度。

部件i+1相對于部件i的角速度是繞轉動關節i+1運動引起的。

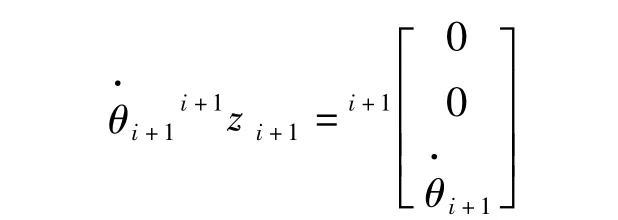
在相同坐標系中，兩個向量可以相互疊加，因此部件i+1的角速度等于部件i的角速度加上部件i+1繞關節i+1轉動的角速度，在{i}中的表示為:

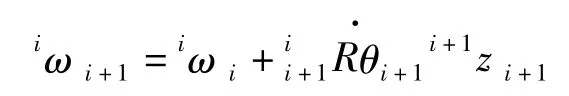
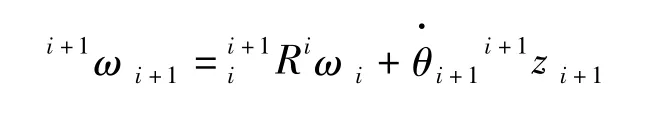
坐標系{i+1}原點的線速度等于坐標系{i}原點的線速度加上部件i因轉動而產生的速度分量，ipi+1表示{i+1}坐標原點在坐標系{i}中的位置矢量，因此得到速度公式:

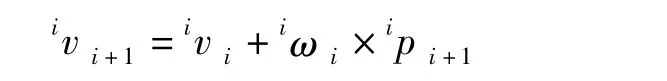
19世紀中葉，統計學形成了兩個主要的學派，數理統計學派與社會統計學派．隨著概率論的成熟，為統計學的發展奠定了數學基礎．19世紀中葉，比利時的阿道夫·凱特勒（1796—1874）主張用自然科學的方法研究社會現象，把古典概率論引入了統計學，使得統計學進入了一個新的發展階段．不過凱特勒將自然科學的觀點與方法機械套用到犯罪、道德等社會問題，混淆了自然現象與社會現象之間的本質區別．盡管如此，凱特勒把概率論引入統計學至少使得統計學在“政治算術”的“算術”方法基礎上往準確化道路邁進了一大步，他為后期數理統計學的形成與發展奠定了基礎．

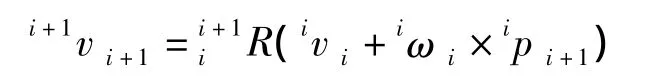
分別對上述公式求微分，即可得出各個部件的角加速度和線加速度的傳遞公式:

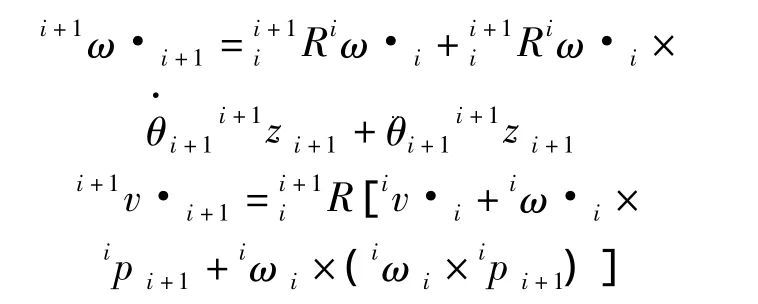
同理，求出部件質心的加速度為:

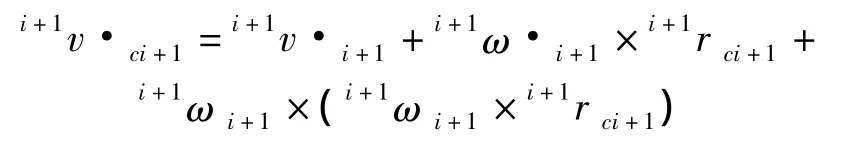
根據牛頓－歐拉方程得出挖臂各個部件之間的力、速度關系通式:

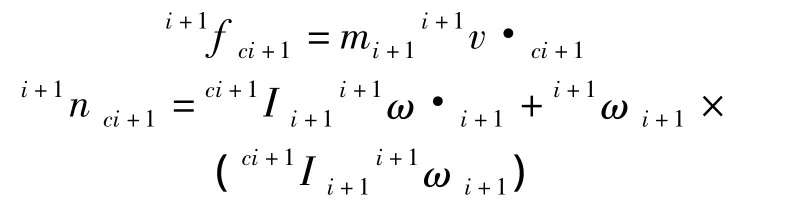
對挖臂進行靜力學分析時，首先對其中一個部件進行受力分析，從而建立部件的靜力學平衡方程。當部件處于力學平衡狀態時，所受到的合力以及合力矩為零。推導出力和力矩的平衡方程為:

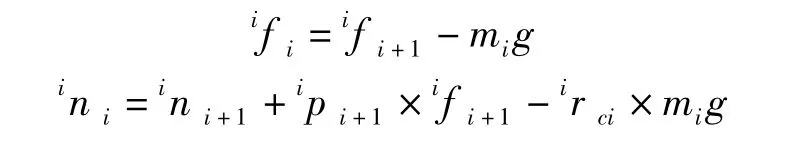
式中，ifi，ini——部件 i受到部件 i－1 的作用力、力矩;

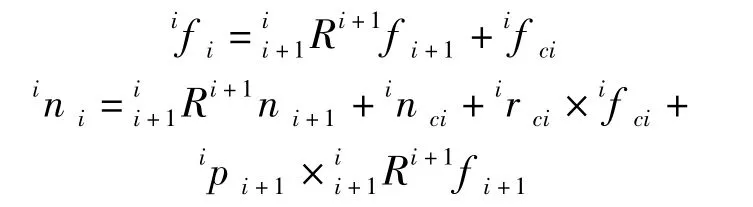
由于{0}固結在水平擺動座上，在x，y平面內，是固定不動的，因而0ω0=0，0v0=0，{4}固結在扒斗的末端，即斗齒尖的位置，得出θ4=0=0。

挖臂運動具有多輸入、多輸出的特點。由于輸入參數的不同，在相同的位置點也會產生不同的速度以及挖掘力。為了更清楚的描述挖臂的速度、力參數與斗齒所在的位置之間的關系，選取一個工作路徑，并分析這個工作路徑上所有連續點的速度以及挖掘力曲線并利用Matlab分析其數據曲線(如圖3～圖4所示)。

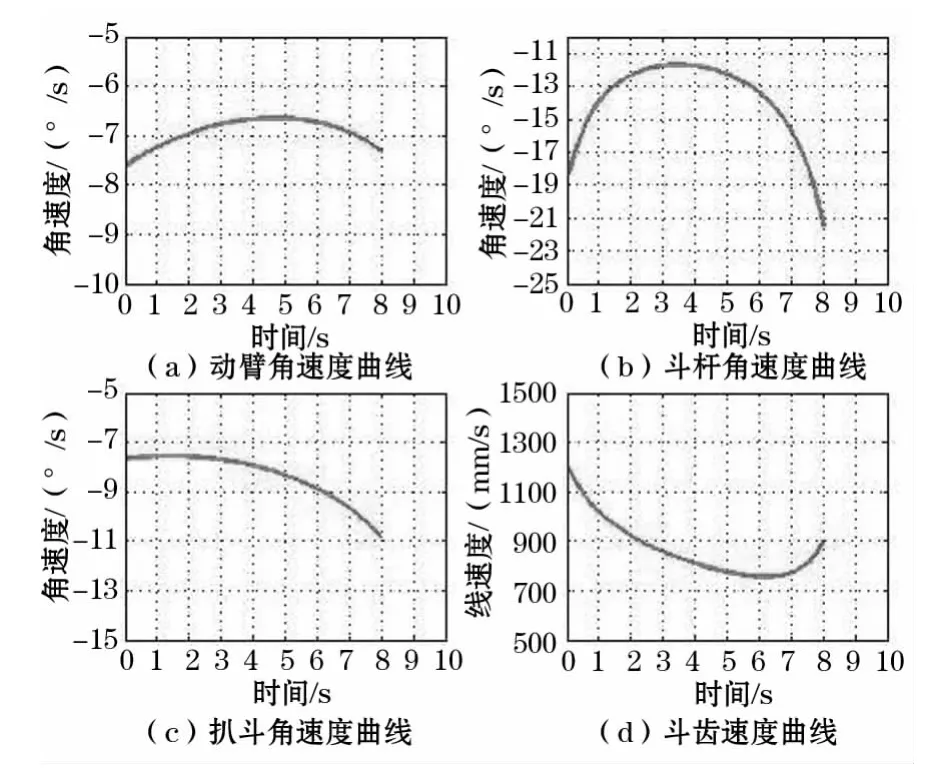
圖3 挖臂速度曲線

圖4 挖臂挖掘力曲線

3 動力學性能優化

在奇異點挖臂會喪失一個或者幾個自由度。在奇異點附近，其動力學性能也會變差;離奇異點越遠，挖臂在各個方向的運動性能和施力效果的一致性愈好。挖臂的動力學性能，對于挖臂結構設計、工作空間選擇、控制方案擬定、液壓系統選型以及軌跡規劃都具有十分重要的作用。挖臂動力學的復雜性不僅在于結構復雜性，還在于煤礦井下除渣作業情況的多樣性和影響因素的可變性。在設計挖臂工作范圍或實現挖臂軌跡控制時，最值得注意的是一些最嚴峻最危險的情況，如最高速度作業時，最大關節驅動力時，挖臂懸伸最長時等，應該考慮這些最壞情況下的作業情況和對動力學的要求。因此，提出了衡量挖臂動力學性能的綜合性能指標以及相應的優化方法。為了說明各種動力學性能指標之間的聯系，根據H.Asada的廣義慣性橢球GIE(generalized inetia tensor ellipsoid)理論來評定挖臂的動力學特征。廣義慣性橢球理論GIE實質上是以笛卡爾慣性矩陣的特征值來描述挖臂在各個方向上的加速特征:

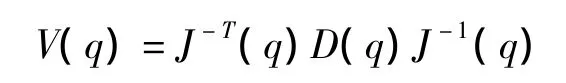
式中，D(q)——操作臂的慣性矩陣，可以通過推導公式求出;

J(q)——雅克比矩陣。

對于n×n的慣性矩陣V(q)，二次型方程:

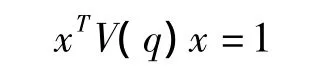
可以表示n維空間中的一個橢球，稱之為廣義慣性橢球GIE。慣性矩陣V(q)特征矢量的方向即為橢球的主軸方向，矩陣V(q)特征值的平方根為橢球主軸的長度。利用廣義慣性橢球GIE來衡量挖臂的加速性能具有明顯的幾何直觀性。在挖臂斗齒的活動空間內的任何一點，根據上述二次型方程可以畫出一個橢球，該點對應橢球的形狀可以衡量其動力學性能的好壞，橢球愈接近球，即主軸長度一致時，動力學性能愈好。廣義慣性橢球的形狀完全是個圓球的點稱為動力學各向同性點，在動力學各向同性點上，慣性矩陣V(q)的列向量互相線性獨立，并且模相等。橢球接近于圓球形時，加速性能變好，近似于各向同性;在工作空間邊緣部分，橢圓變扁，動力學性能變差，圖5為鉆裝機挖臂部分空間位置的廣義慣性橢球圖。

4 結論

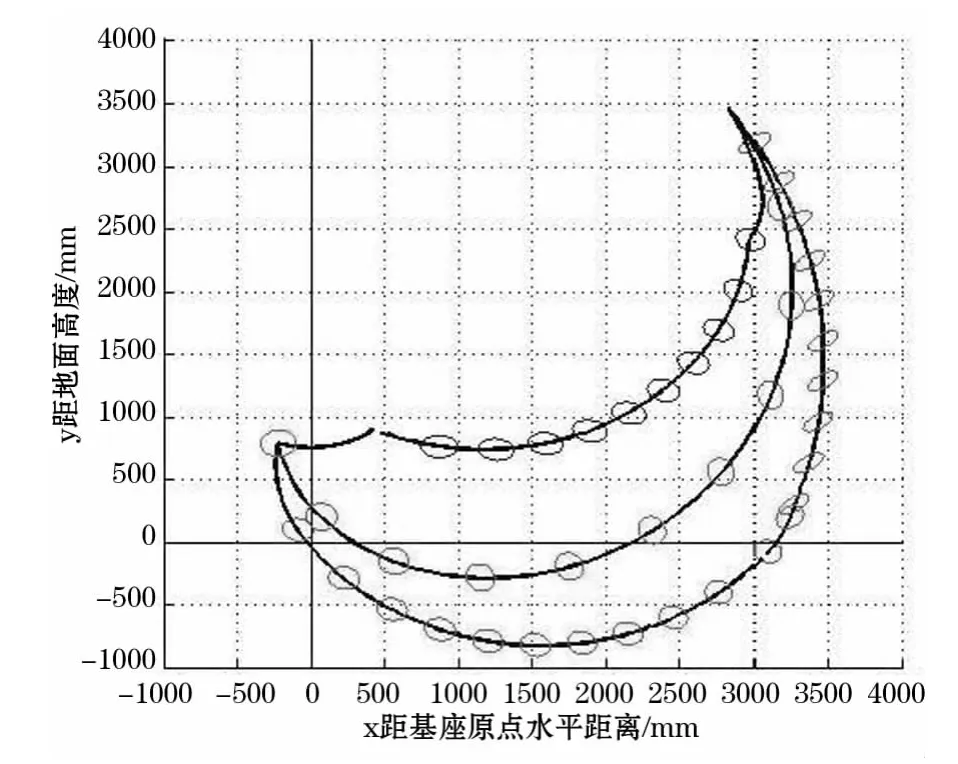
圖5 挖臂空間慣性橢球圖

基于D－H法，建立兩個相鄰部件之間的空間變換關系，并以此推導出斗齒在基礎坐標系內的活動范圍，做出斗齒的工作空間包絡圖。利用牛頓－歐拉方程建立挖臂的動力學方程，并借助MATLAB軟件進行動力學仿真計算，得出動臂、斗桿、扒斗的驅動力矩變化規律，分析出斗齒末端的速度、力曲線。最后利用廣義慣性橢球理論，評價挖臂在整個工作空間的動力學性能，為挖臂的機械結構設計、工作空間的選擇、作業軌跡規劃和控制方案的擬定提供數據參考。

［1］熊有倫，丁 漢.機器人動力學性能指標及其優化［J］.機械工程學報，1989，25(2):9-15.

［2］Asada H.A Geometrical Represantation of Manipulator Dynamics and its Application to Arm Design［J］.Trans.Of ASME J.Optimiation of Dynamic Systems，Measurement and Control，1983，105(3):140-145.

［3］John J.Craig.Introduction to Robotics Mechanics and Control Third Editoin［M］.London:Pearson Education Ltd，2005.

［4］楊 武，蔣梁中.采用牛頓－歐拉法的排爆機器人機械手動力學分析［J］.現代制造工程，2010(6):140-143.

［5］黃 真，趙永生，趙鐵石.高等空間機構學［M］.北京:高等教育出版社，2006.

［6］任曉華，任運濤.鉆裝機耙渣工作裝置運動學仿真分析［J］.煤礦機械，2012，33(4):69-71.