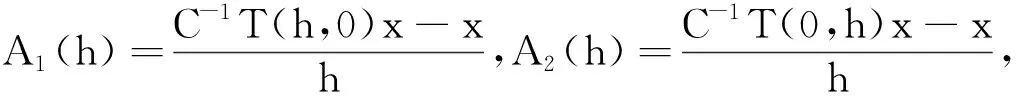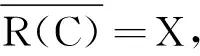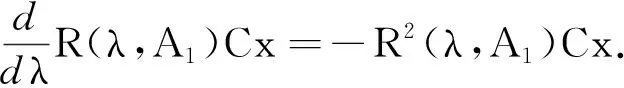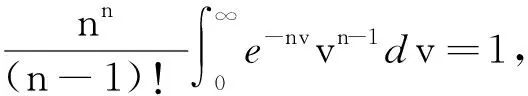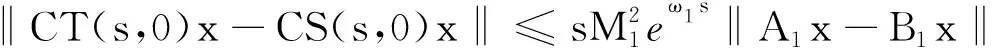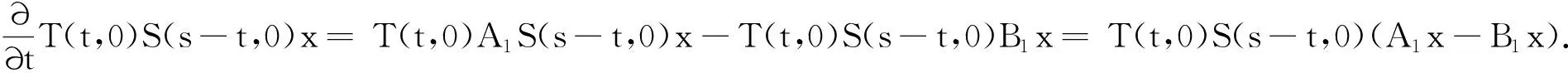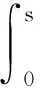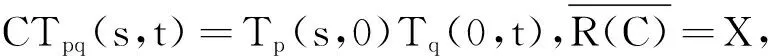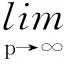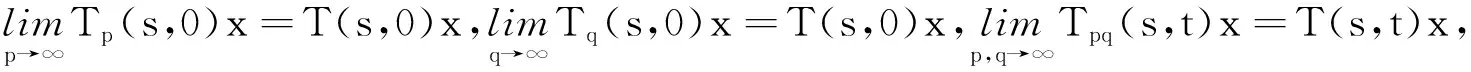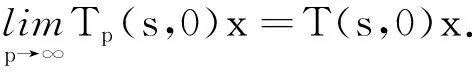指數有界雙參數C半群的逼近
岳 田,宋曉秋
(中國礦業大學理學院,中國 徐州 221116)
自Hille[1]首先提出算子半群理論以來,其理論得到不斷豐富和發展.尤其是近年來,受一些具體問題如具有非稠定算子的抽象Cauchy 問題的激發,已有10余種算子半群或算子族相繼被國內外眾多學者廣泛關注,并取得了一系列成果[2-11].其中對于算子半群逼近問題的討論,有力地推動了大量實際問題的研究,如在平面上的Markov擴散過程,人類學中的人口發展問題,物理學中的中子遷移系統漸近狀態的研究等方面顯示出較好的實際意義.
眾所周知,經典的單參數算子半群理論已日益完善,并得到了廣泛應用.與其相比,雙參數半群理論研究進展緩慢,還有許多不完善之處,近些年來,已有一些學者對其進行了初步研究.如文獻[5]給出了雙參數強連續算子半群的定義及其與生成元之間關系的若干性質;文獻[6]給出了雙參數強連續算子半群的預解式的系列性質;文獻[7]介紹了雙參數強連續算子半群的收斂性問題;文獻[8]對雙參數C半群的基本性質及Cauchy問題進行了討論.本文在上述文獻的基礎上,結合單參數C半群的相關理論,討論了指數有界的雙參數C半群的逼近定理.
1 定義及相關引理
在本文中,設(X,‖·‖)為Banach空間,L(X)表示所有從X到自身的線性算子的全體,記B(X)為X上一切有界線性算子構成的Banach代數.設A為X中的線性算子,D(A) ,R(A) ,R(λ,A) 分別表示定義域,值域及預解式.算子C∈B(X)為單射,記ρC(A)為A的C預解集,其中ρC(A)={λ:λ-A為單射且R(C)?R(λ-A)}. (λ-A)-1C為A的C預解式,R+2表示二維非負實數空間.
定義1[8]若雙參數算子族{T(s,t)}s,t≥0?B(X)滿足:
1)T(0,0)=C;
2)T(s+s′,t+t′)C=T(s,t)T(s′,t′),?s,s′,t,t′≥0;
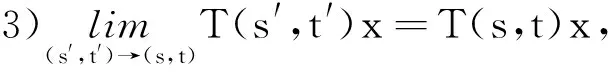
則稱其為X上的雙參數C半群.
進一步地,若存在M≥‖C‖,ω∈R,使得對?s,t≥0,有‖T(s,t)‖≤Meω(s+t),則稱雙參數C半群{T(s,t)}s,t≥0為指數有界的雙參數C半群.
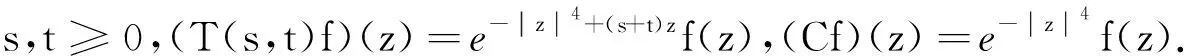
對任意的s,t≥0 ,由定義1中性質2)可得
T(s,t)C=T(s,0)T(0,t)=T(0,t)T(s,0),T(s,0)C=CT(s,0),T(0,t)C=CT(0,t),
這意味著{T(s,0)}s≥0和{T(0,t)}t≥0是2個可交換單參數C半群.對此,不妨設A1和A2分別是單參數C半群{T(s,0)}s≥0和{T(0,t)}t≥0的無窮小生成元,那么
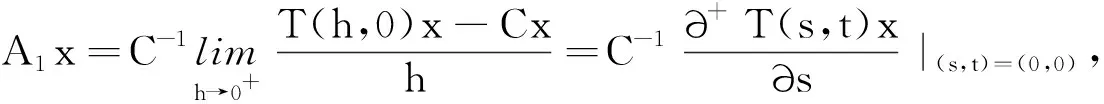
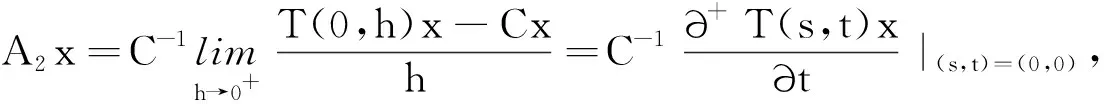
這里,
定義2雙參數C半群{T(s,t)}s,t≥0的無窮小生成元A定義如下:
引理1雙參數C半群{T(s,t)}s,t≥0的無窮小生成元是線性變換L:R+2→L(X) ,其定義為L(a,b)x=(A1,A2)(a,b)Tx=aA1x+bA2x,?x∈X,(a,b)∈R+2.這里,算子A1和A2分別是單參數C半群{T(s,0)}s≥0和{T(0,t)}t≥0的無窮小生成元.
證類似文獻[5]中定理2.3.
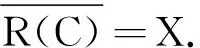
證設‖T(t)‖≤Meωt,其中ω≥0 ,A是T(t)的無窮小生成元.因為對每一h>0,A(h)有界,故etA(h)是可定義的.而且由于A(h)與T(t)可交換, etA(h)和T(t)亦是如此.又
因此對于0 所以對于0 tM2exp{t(eω+ω-1)}‖Ax-A(h)x‖. 證因為對每一h>0 ,A1(h)和A2(h)均是有界的,故esA1(h)和etA2(h)是有意義的,且二者是可交換的.則對?x∈X有 ‖C2esA1(h)etA2(h)x-CT(s,t)x‖=‖C2esA1(h)etA2(h)x-T(s,0)T(0,t)x‖≤ ‖C2esA1(h)etA2(h)x-T(s,0)CetA2(h)x‖+‖T(s,0)CetA2(h)x-T(s,0)T(0,t)x‖≤ ‖CetA2(h)‖‖CesA1(h)x-T(s,0)x‖+‖T(s,0)‖‖CetA2(h)x-T(0,t)x‖. 又因為A1(h)和A2(h)是有界可交換的,故esA1(h)etA2(h)=esA1(h)+tA2(h),?h>0.進而有 且上述極限在s,t的任何有限區間上的收斂是一致的. 即 定理3設(A1,A2),(B1,B2)分別是雙參數C半群{T(s,t)}s,t≥0和{S(s,t)}s,t≥0的無窮小生成元,若 1)對于s≥0,有‖T(s,0)‖≤M1eω1s,‖S(s,0)‖≤M1eω1s; 2)對于s≥0,x∈X,有T(s,0)S(s,0)=S(s,0)T(s,0). 證當x∈D(A1)∩D(B1)時,此時可將雙參數C半群T(s,0),S(s,0)視為單參數C半群.則如下等式成立: 上式兩端從0到s積分可得 則有 1)對于s,t≥0,有‖T(s,0)‖≤M1eω1t,‖Tp(s,0)‖≤M1eω1t; 2)對于s,t≥0,有‖T(0,t)‖≤M2eω2t,‖Tq(0,t)‖≤M2eω2t; 3)D(A1)?D(Ap),D(A2)?D(Aq)(p,q∈N); 4)對于s,t≥0,有T(s,0)Tp(s,0)=Tp(s,0)T(s,0),T(0,t)Tq(0,t)=Tq(0,t)T(0,t); 證當x∈D(A1)∩D(Ap),且0≤s≤T時,可將雙參數C半群Tp(s,0),T(s,0)視為單參數C半群.從而由定理3可得 參考文獻: [1] HILLE E, PHILLIPS R S. Functional analysis and semigroups[M]. New York: Am Math Soc Colloq Pub,1957. [2] PAZY A. Semigroups of linear operators and applications to partial differential equations[M]. New York: Springer-verlag, 1983. [3] PFEIFER D. Approximation-theoretic aspects of probabilistic representations for operator semigroups[J].J Approx Theory, 1985,43(3):271-296. [4] ADRENT W. Vector-valued Laplace transforms and Cauchy problems[J]. Isr J Math, 1987,59(3):327-352. [5] SHARIF A S, KHALIL R. On the generator of two parameter semigroups[J]. Appl Math Comput, 2004,156(2):403-414. [6] 蔡 亮,宋曉秋,禹曉紅.雙參數C0半群的指數公式與預解式[J]. 徐州師范大學報, 2010,28(4): 43-45. [7] 禹曉紅,宋曉秋,李玉霞,等.雙參數C0半群的收斂性問題[J]. 貴州大學學報, 2011,28(3):4-6. [8] JANFADA M. On two-parameter regularized semigroups and the cauchy problem[J]. Abstract Appl Anal, 2009,2009:1-15. [9] LI Y C, SHAW H Y. N-times integrated C-semigroups and the abstract cauchy problem[J]. Taiwan J Math, 1997,1(1):75-102. [10] 陳文忠.C-無窮小生成元的表示式[J]. 廈門大學學報, 1993,32(2):135-140. [11] 徐景實,周放軍. Toeplitz型算子在變指數空間的有界性[J]. 湖南師范大學自然科學學報, 2011,34(1):1-4.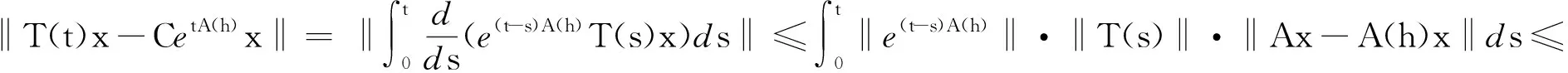
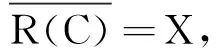
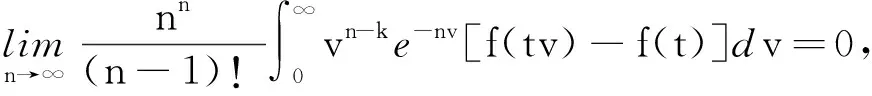
2 主要結論