基于徑向基神經網絡的艦艇磁場推算模型＊

（91388部隊 湛江 524022）

1 引言

近年來，閉環消磁技術成為各國消磁研究熱點，相較于目前的消磁系統控制方法，它可以實現固定磁場的實時補償，是未來磁隱身技術發展的必然趨勢。為了獲取較多的艦船內部信息，以及實際中艦船內部傳感器的安裝問題，傳感器應該與船殼非常接近，測量所得的磁場是艦艇內部復雜的近場值。相對于目前較成熟的磁場深度推算問題，內外磁場推算屬于不同的半空間，且存在磁屏蔽現象，很多深度換算中的成功模型（如：磁偶極子等）難以直接應用［1］。因此，尋找一種根據艦船內部磁場測量值有效推算艦船外部某特定深度上磁場的方法成為實現閉環消磁技術的關鍵，也是閉環消磁技術亟待解決的問題之一。

國外對艦艇內外換算方法較早進行了研究，文獻［1］利用積分方程法，建立了基于薄殼體內外換算的一種有效模型，但它只解決了船殼內外感應磁場換算的問題，對于固定磁場以及增加設備后的艦船內外磁場沒有進行深入研究。文獻［2］提出了一種利用虛擬磁源法（Virtual source）建立艦船磁場內外換算的數學模型，但只進行了原理說明，沒有具體的實驗驗證其換算精度。文獻［3］在文獻［2］的基礎上，進行了理論上的改進，其主要原理是利用當前磁化狀態下的艦船內部磁場與內部校準矢量（Onboard Calibration Vector）計算得到比例系數（Scale Factor），將所得的比例系數與外部校準矢量（Offboard Calibration Vector）相乘，就可得到當前艦船外部磁場值。文獻［4］從磁勢的角度出發，建立了雙層殼潛艇的感應磁場直接計算模型，并反演出固定磁場值，其換算精度較高，但其要求鐵磁材料的一些重要參數為已知，而這些參數在實際中一般很難得到。國內對閉環消磁技術的研究尚處于起步階段，文獻［5］在文獻［3］的基礎上，通過船模實驗驗證了基于變化量的校準矢量進行磁場推算的有效性。文獻［6］從位置優化的角度出發，對薄鋼板兩側磁場推算進行了研究，提高了薄鋼板兩側磁場推算精度，但尚未涉及船模的內外磁場換算研究。上述文獻大多是采用線性化方法解決內外換算問題，可能會面臨網格剖分、復雜的重積分計算、反演過程中方程不適定以及對于數據具有選擇性等問題，且隨著艦船的大型化，鐵磁設備多樣化將會加劇線性建模的難度，影響其換算精度。本文從智能優化的角度出發，建立了內外磁場之間的RBF神經網絡預報模型。該方法避免了利用數值建模技術存在的諸多困難，即可實現艦艇內外磁場的換算，相較于其他數值建模方法其換算精度有所提高，并利用船模實驗驗證了所得網絡的有效性和良好的泛化能力。

2 艦船磁場內外推算的數值模型

文獻［3］中提到的校準矢量法具有原理簡單、換算方便（不必網格剖分，不涉及復雜重積分計算）等優點，本文選取校準矢量法作為數值建模的代表。該方法從虛擬磁源的理論出發，認為艦艇內外磁場均是由磁源產生的，如圖1所示為內外磁場換算示意圖。

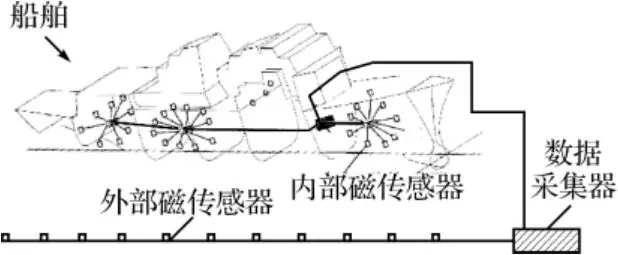
圖1 艦船磁場內外換算示意圖

當磁場大小發生改變時，代表磁源的大小或方向發生改變，而內外傳感器的位置相對于磁源位置是相對固定的，用矩陣表示如方程（1）所示

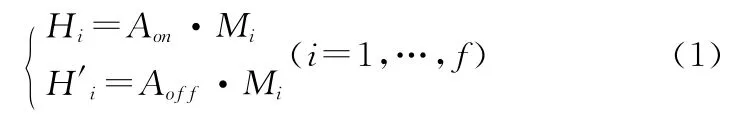
其中，Mi代表磁源在第i種磁化狀態下的磁矩列向量，Hi、H′i分別代表艦船內、外部磁場強度值組成的列向量，Aon、Aoff分別代表聯系磁矩列向量與磁場強度的線性觀測矩陣，矩陣中的每個元素由內外傳感器布設位置與磁源布設位置決定。選取一部分磁化狀態下的Hj與H′j（j＝1，…，m，1＜m＜f）分別作為內、外校準矢量，則某一磁化狀態下，內、外磁場強度值Hk與H′k（k?j）與內、外校準矢量Hj與H′j之間的比例關系為

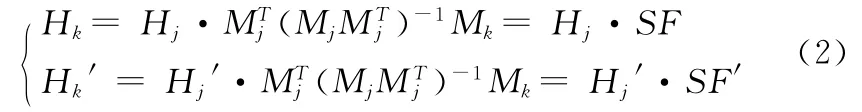
其中SF、SF′分別代表內、外部比例系數矩陣，觀察方程組（2）發現，對相同磁化狀態下的一組內外磁場列向量而言SF＝SF′。則可以先通過Hk與Hj反演出SF，將其代入方程組（2），即可獲得內、外磁場強度值Hk與H′k（k?j）之間的換算關系為

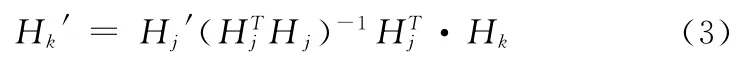
綜上所述為目前國內外學者針對內外換算問題提出的較先進的線性建模方法，其誤差主要來源于測量誤差以及反演校準矢量SF時方程不適定造成的誤差。與最常用的BP神經網絡相比，RBF［7～10］神經網絡在逼近能力、分類能力和學習速度方面均優于BP 網絡，為此選擇該網絡作為智能優化的代表。

3 RBF神經網絡模型基本原理

RBF神經網絡是一種具有單隱層的三層前饋網絡，它模擬了人腦中局部調整、相互覆蓋接受域的神經網絡結構，由輸入層、具有徑向基函數神經元的隱層和具有線性神經元的輸出層構成，如圖2所示為一個典型的RBF神經網絡結構圖。徑向基層單元的作用函數常取高斯基函數，可表示為如下形式：

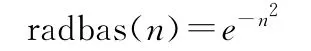
神經元radbas的輸入為輸入向量p與隱層權值w1之間的距離（dist函數）與隱層閾值b1的乘積；輸出層神經元傳遞函數為purelin，輸出層權值為w2，輸出層閾值為b2。選擇Matlab工具箱中的newrb（）函數設計網絡，該函數包含輸入樣本、期望輸出、訓練精度Goal和散布常數spread幾個關鍵變量。其中散布常數的選擇尤為重要，如果散布常數選擇不當，會造成網絡設計中神經元數過多或過少，進而在函數逼近中造成過適性或不適性，一般情況下，散布常數的選取取決于輸入向量之間的距離，要求是要介于最小距離與最大距離之間。

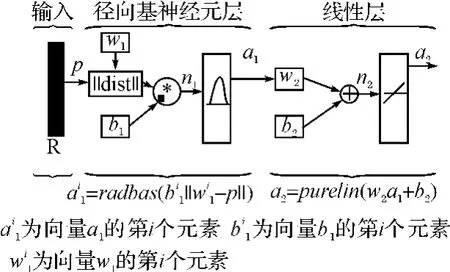
圖2 徑向基網絡結構圖

4 神經網絡預報模型的有效性驗證

4.1 基于RBF神經網絡的潛艇磁場內外換算實驗設計

選取一兩端封閉的空心圓筒作為潛艇模型（長2002mm，厚6mm），選用一可以自由推入推出圓筒的測量架，以便布設內部磁傳感器。將七個傳感器等間距布設在測量架中心線位置，將其推入空心圓筒內部，用以測量潛艇模型內部磁場，并在模型正下方0.594m處，等間距布設七個傳感器用以測量潛艇外部磁場，磁傳感器具體布設如圖3所示。

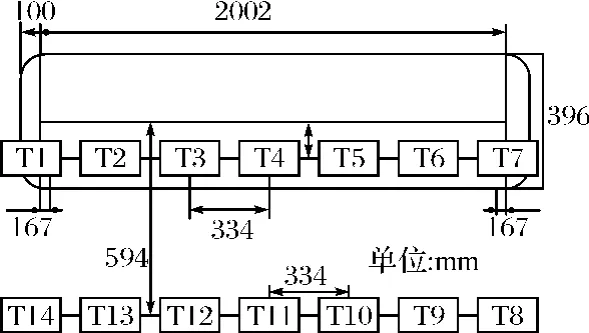
圖3 傳感器布設示意圖

4.2 RBF網絡基本參數的確定

通過改變敷設在船模外部導線中的電流來模擬模型固定磁化狀態的變化。在得到12組不同磁化狀態下模型的內外測量數據后，任意選取其中11組內外測量數據作為A組，剩余1組內外測量數據作為B組。則RBF神經網絡的基本參數選取規則如下：

訓練樣本集：選取A組中的內部測量數據即文獻［5］中的內部校準矢量Hj作為訓練網絡的學習樣本，A組中的外部測量數據即文獻［5］中的外部校準矢量Hj′作為訓練網絡的期望輸出；

測試樣本集：選取B組中的內部測量數據即文獻［5］中的Hk作為測試網絡訓練效果的輸入樣本，B組中的外部測量數據Hk′即文獻［5］中的作為網絡的理想輸出；

訓練精度Goal：Goal＝0.00001；

散布常數spread：0.001。

4.3 網絡訓練以及網絡評價

基本參數設置完畢后，輸入學習樣本訓練網絡，而后輸入測試樣本來測試網絡的預測精度。為了方便與文獻［5］中校準矢量法進行比較，本文選擇與文獻［5］中相同的最大相對均方根誤差ERR 作為衡量預測精度的判定依據，其中ERR 定義為

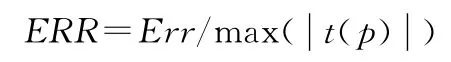
則12組利用校準矢量法的磁場推算誤差［5］與本文提出的RBF神經網絡預報誤差比較圖如圖4所示，由圖可見，RBF神經網絡預測精度均優于校準矢量法磁場的推算精度，前者的ERR 最大值不超過3%，且大部分ERR 小于1%，而后者ERR 最大值大于6%，從而驗證了基于RBF神經網絡推算方法的有效性。且該方法的預報誤差分布均勻，誤差曲線較為平緩，說明RBF神經網絡選用不同的基函數作為訓練樣本對預報結果影響較小。

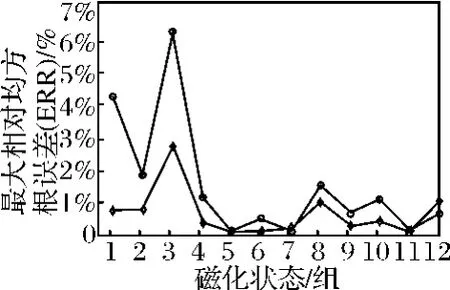
圖4 兩種方法建模時，ERR 比較圖

5 結語

本文先從數值建模角度研究了艦船內外磁場之間的關系，利用數值建模技術會存在反演模型不適定的問題，且對于同一組數據而言，選擇不同的校準矢量對換算結果影響較大。鑒于此，本文從智能優化的角度出發，建立了內外磁場之間的RBF神經網絡預報模型，并通過船模實驗驗證了網絡預測的準確性，相較于線性方法，換算精度有所提高，且有較高的穩定性，符合工程實際需求。

［1］Oliver C，Jeanlouis C，Jeant B，et al.Recent improvements for solving inverse magneto static problem applied to thin shells［J］.IEEE Transactions and Magnetics，2002，38（2）：1005-1008.

［2］Carl S.Closed-loop multi-sensor control system and method［P］.US PATENT 5189590Feb.23，1993.

［3］Richard M，Robert A.Ship degaussing system and algorithm［P］.US PATENT 6965505B1Nov.15，2005.

［4］Vuillerunet Y，Closed loop degaussing applied to double hull submarine magnetization identification from near magnetic fields measurements［D］.Grenoble，2008：25-30.

［5］王鯨，劉勝道，蘇廣東.一種潛艇內外磁場換算算法的實驗驗證［J］.海軍工程大學學報，2010，22（1）：83-86.

［6］Wang Jing，Liu Shengdao，Su Guangdong.The Experimental Validation of Submarine’s Inside Magnetic Field Extrapolation from outside Magnetic Field［J］.Journal of Naval University of Engerneering，2010，22（1）：83-86.

［7］連麗婷，肖昌漢，劉勝道等.基于微粒群算法的薄鋼板兩側磁場推算中的位置優化［J］.上海交通大學學報，2010，44（7）：0975-0979.

［8］董長虹.Matlab神經網絡與應用［M］.北京：國防工業出版社，2007：64-110.

［9］Dong Changhong.Matlab Neural Networks and Applications［M］.Beijing：National Defense Industry Press，2007：64-110.

［10］張利平，孫美鳳，王鐵生.新型的RBF神經網絡在水輪發電機組故障中的應用［J］.水力發電學報，2009，28（6）：219-224.

［11］耿志強，朱群雄，顧祥柏，等.基于多群競爭PSO-RBFNN 的乙烯裂解深度智能優化控制［J］.化工學報，2010，61（8）：1942-1948.

［12］夏紅霞，王惠營，胡磊.基于粗糙集的神經網絡結構優化方法［J］.計算機與數字工程，2010，38（5）.

［13］韓紅桂，喬俊飛，薄迎春.基于信息強度的RBF神經網絡結構設計研究［J］.自動化學報，2010，22（1）：83-86.