Mathematica軟件在多元函數微分學中的應用

辛春元

（遼寧對外經貿學院，遼寧 大連 116052）

一、Mathematica軟件在多元函數微分學中的基本命令[1]

1 Mathematica軟件計算的基本命令

D[f,var](求函數f對自變量var的偏導數)；

D[f,X1，X2，…](求函數 f對自變量 X1，X2，…的混合偏導數)；

D[f,{X1，n1},{X2，n2},…](求函數 f對自變量 X1，X2，…的n1,n2,…階混合偏導數).

Dt[f]求f的全微分；

Dt[f，var]求 f對自變量 var的全微分,其中f的各元都是var的函數；

SetAttributes[c,Constant]聲明c是常數.

2 Mathematica軟件繪制圖形的基本命令

Plot3D[f,{x,xmin,xmax},{y,ymin,ymax},options](繪制三維圖形的函數)；

ParametricPlot3D[{x(u,v),y(u,v),z(u,v)},{u,umin,umax},{v,vmin,vmax}](繪制參數方程圖形的函數)；

ContourPlot[f[x,y],{x,x1,x2},{y,y1,y2}]（在平面上作二元函數的等高線）.

二、Mathematica軟件在多元函數微分學中的應用

1 Mathematica軟件的計算功能在多元函數微分學中的應用

解輸入

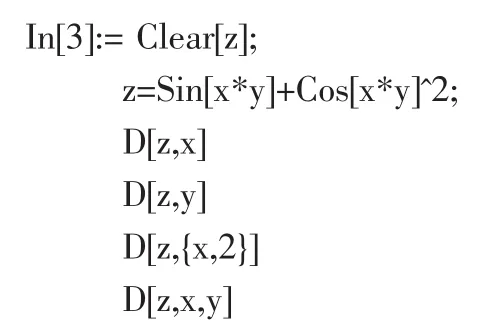
則輸出所求結果為

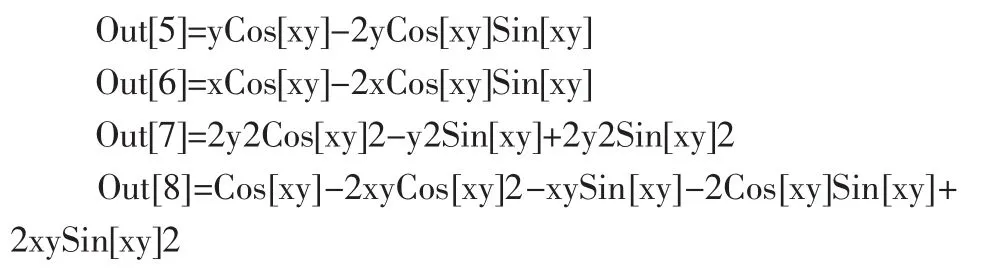
實例2設其中a是常數,求dz.[2]

解輸入

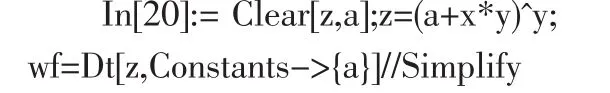
則輸出結果為

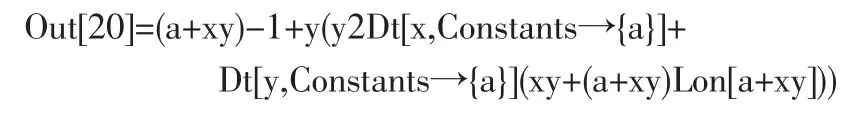
其中 Dt[x,Constants->{a}]就是 dx,Dt[y,Constants->{a}]就是dy.可以用代換命令“/.”把它們換掉.輸入

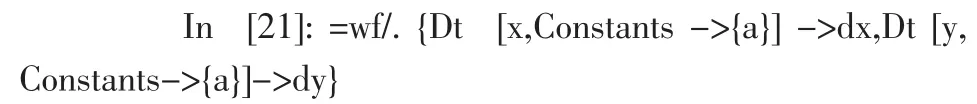
則輸出結果為

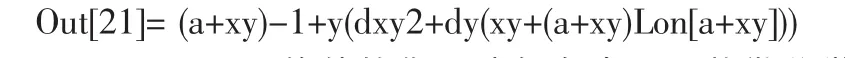
2.2 Mathematica軟件的作圖功能在多元函數微分學中的應用

實例3求出曲面在點(1,1)處的切平面、法線方程,并畫出圖形.[3]

解 首先畫出曲面的圖形.

輸入命令

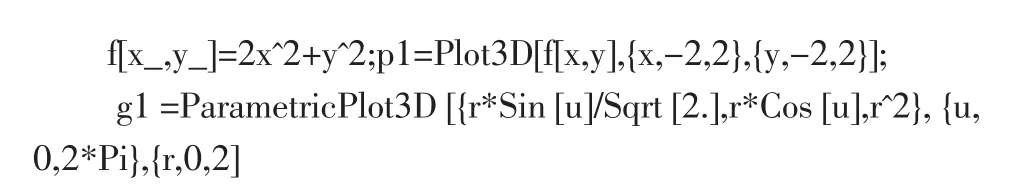
則輸出相應圖形(圖1).

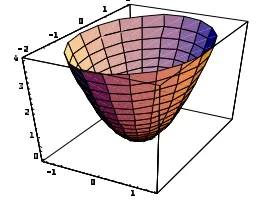
圖1

其次畫出切平面的圖形.輸入命令

則輸出切平面方程為及相應圖形（圖2）.

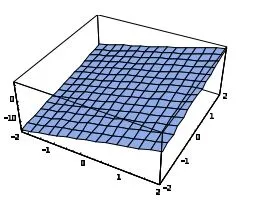
圖2

最后畫出法線的圖形.輸入命令

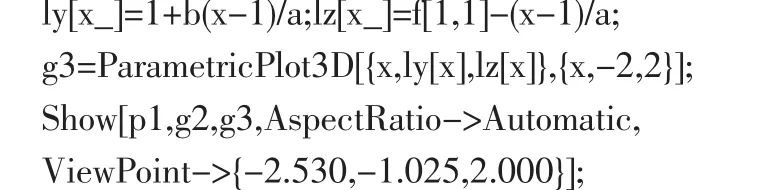
則輸出相應圖形(圖3).

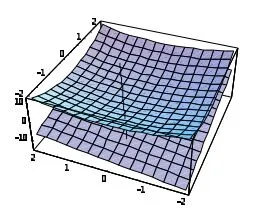
圖3

解 輸入命令

則輸出相應圖形（圖4），其中

(1)u（x·y）的梯度與等高線圖;

(2)v（x·y）的梯度與等高線圖;

(3)u（x·y）與 v（x·y）的等高線圖;

(4)u（x·y）與 v（x·y）的梯度圖.

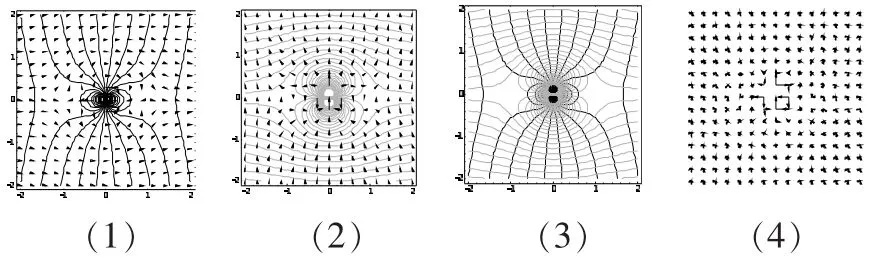
圖4

從上述圖中可以看出它們的等高線為一族正交曲線.事實上,有且它們滿足拉普拉斯方程

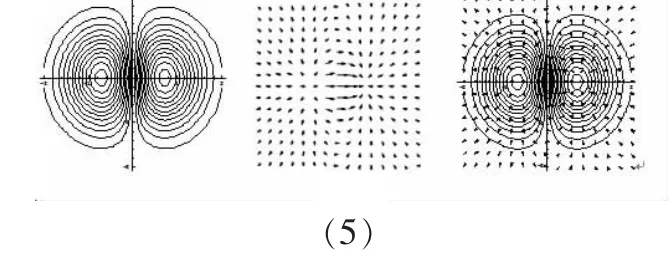
實例5設作出的圖形和等高線,再作出它的梯度向量gradf的圖形.把上述等高線和梯度向量的圖形疊加在一起,觀察它們之間的關系.[2]

輸入調用作向量場圖形的軟件包命令

輸出為圖8.從圖可以看到平面上過每一點的等高線和梯度向量是垂直的,且梯度的方向是指向函數值增大的方向。

三、小結

總之，利用Mathematica軟件強大的計算功可以求多元函數偏導數、全微分、二元函數極值等等，利用Mathematica軟件的作圖功能能夠直觀的理解曲面的切平面、方向導數、梯度和等高線等概念，降低學習難度，提高解決實際問題的綜合能力。

[1]丁大正.科學計算強檔Mathematica4教程[M].北京：電子工業出版社 2002，3.

[2]吳贛昌.微積分[M].北京：中國人民大學出版社2012，6.

[3]章棟恩 許曉革.高等數學實驗 [M].北京：高等教育出版社2004，7.