移動信標改進的DV－Hop算法

陳志國，傅 毅，2，須文波，孫 俊

（1.江南大學 物聯網工程學院 輕工過程先進控制教育部重點實驗室，江蘇 無錫214122 2.無錫環境科學與工程研究中心，江蘇 無錫214063）

0 引 言

目前無線傳感器網絡 （wireless sensor network，WSN）由于靈活性大、容錯性強等特點廣泛應用于醫療、交通、軍事等領域[1]。WSN的應用以數據采集為前提，但 WSN的節點布設隨機性強，所以節點如何知道自身位置成為問題的關鍵和目前的研究熱點[2]。

WSN的節點定位一般分為基于測距的 （range－based）定位和無需測距的 （range－free）定位兩大類，由于無需額外的硬件，因此實際應用中以后者為主，其中DV－Hop算法備受關注[3]。DV－Hop算法是基于跳數原理的距離無關定位算法，由于后期采用的三邊測量法會產生一定的誤差，因此一些智能算法逐漸被引入以降低誤差，如遺傳算法[4]、PSO算法[5]和 QPSO[6]算法改進的 DV－Hop算法。本文將采用一種改進的QPSO算法來降低DV－Hop算法的定位誤差。定位精度是WSN的一項重要指標，但節點開銷也不容忽視，采用移動信標可以大大降低成本，因此本文還提出了一種基于虛擬力的信標移動新方法來降低系統開銷。

1 DV－Hop算法模型

DV－Hop算法的基本原理是先通過計算跳數獲得網絡拓撲信息，然后用三邊定位法獲得未知節點信息[7]。跳數計算過程如下:①每個信標節點將自己的位置信息包向外進行廣播，初始時跳數為0，收到信息包的節點更新自己的信息表；②繼續上一次的廣播過程，信息包每轉發一次跳數就加1；③節點收到新信息包時先查看自己的信息表里是否已有該信息包的標識，若有且新信息包的跳數值更小，就更新跳數值；否則新數據包被忽略，停止轉發。

按照這種規則進行全網內跳數廣播，便得到錨節點到其他所有錨節點的跳數和位置。根據位置坐標，錨節點i可以計算出他們之間的距離，然后每一個錨節點按公式 （1）計算平均每跳距離

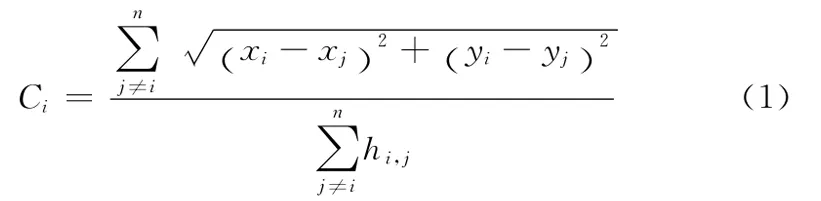
其中 （xi，yi）是錨節點i的坐標，（xj，yj）是除錨節點i之外的錨節點坐標，hi，j是錨節點i到錨節點j之間的跳數，n是錨節點總數。然后錨節點i向鄰居節點廣播平均每跳距離，由于數據包里含有錨節點自身標識和平均每跳距離，其他節點收到該數據包時先比對標識，若標識不重復就向鄰居節點繼續廣播，否則丟棄該數據包。這樣網絡中的每一個節點都知道了所有n個錨節點計算出的平均每跳距離，對這些平均每跳距離取平均值作為自己的每跳平均距離。

之后，未知節點得到了其距離所有n個錨節點的每跳平均距離矩陣和跳數矩陣。對某一個錨節點的跳數與每跳平均距離的乘積就是該節點到錨節點的距離[9]，通常采用三邊測量法或多邊測量法。然后根據最小二乘法原理，求出未知節點的最小二乘位置估計。

由于上述DV－Hop算法采用的三邊或多邊測量方法會產生較大的誤差，為了進一步提高定位精度，這里將引入一種改進的QPSO智能算法對Dv－Hop算法的測量結果進行優化，以提高節點的定位精度。

2 BDQPSO改進DV－Hop節點定位算法

2.1 BDQPSO算法的提出

QPSO算法是J.Sun等人提出的一種改進的粒子群優化 （particle swarm optimization，PSO）算法[10]，該算法從量子力學的角度出發對PSO算法的缺點進行改進，具有較好的優化結果，獲得了廣泛應用。為了進一步提高QPSO算法的收斂精度和全局搜索能力，這里提出一種最佳維改進的 QPSO 算 法:BDQPSO （best dimension quantum－behaved particle swarm optimization）算法。雖然QPSO算法的收斂速度較快，但后期收斂速度會明顯變慢，當接近全局最優位置時可能導致粒子停滯在局部最優位置。這里提出一種新的方法，最佳維 （best－dimension，BD）擾動技術，它可以在QPSO迭代時找到最佳維來執行擾動。具體的BD算法流程描述如下:

（2）在選定粒子位置矢量中隨機選擇s維進行變異，產生s個變異的粒子XM＝（XM1，XM2，…，XMs），其中minX）＋minX；

（3）從s個變異粒子XM和父代粒子Xit中，選出最好適應度的粒子，計算最好適應度值

為了測試BDQPSO算法性能，用表1的標準測試函數對算法進行分析，同時與QPSO算法進行對比。測試過程中，粒子群數量設定為50，維數設定為10、20、50和80，迭代次數設定為200、500、1000、2000，算法每次獨立運行100次，結果見表2。實驗環境為:Pentium E5300 2.6 GHZ，2G內存，MATLAB7.04，操作系統為Win7 32位。從表2可見，BDQPSO算法比QPSO算法具有更好的收斂精度，因此更適合于對DV－Hop算法的定位結果進行優化。

表1 標準測試函數

2.2 基于BDQPSO改進的DV－Hop算法

簡單的節點定位過程只需要兩個步驟，即確定未知節點到錨節點的距離和計算未知節點位置。在第二步中，由于現實環境的不確定性，三邊測量或者多邊測量方法會產生一定的誤差，為了提高定位精度，本文用收斂性更好的BDQPSO算法對DV－Hop算法進行改進。

適應度函數值是評價算法得到的解的優劣程度的標準，這里評價未知節點定位精度的標準是該節點與其他所有錨節點的距離與第一步中由DV－Hop算法得到的距離的累計誤差，該誤差越小則定位精度越高，該適應度函數表示如下

其中Pi是錨節點位置坐標，n為錨節點數量，xj是未知節點的位置坐標，D（j，i）為未知節點j到錨節點i的距離。f（xj）代表未知節點到所有n個錨節點的距離的累計誤差。

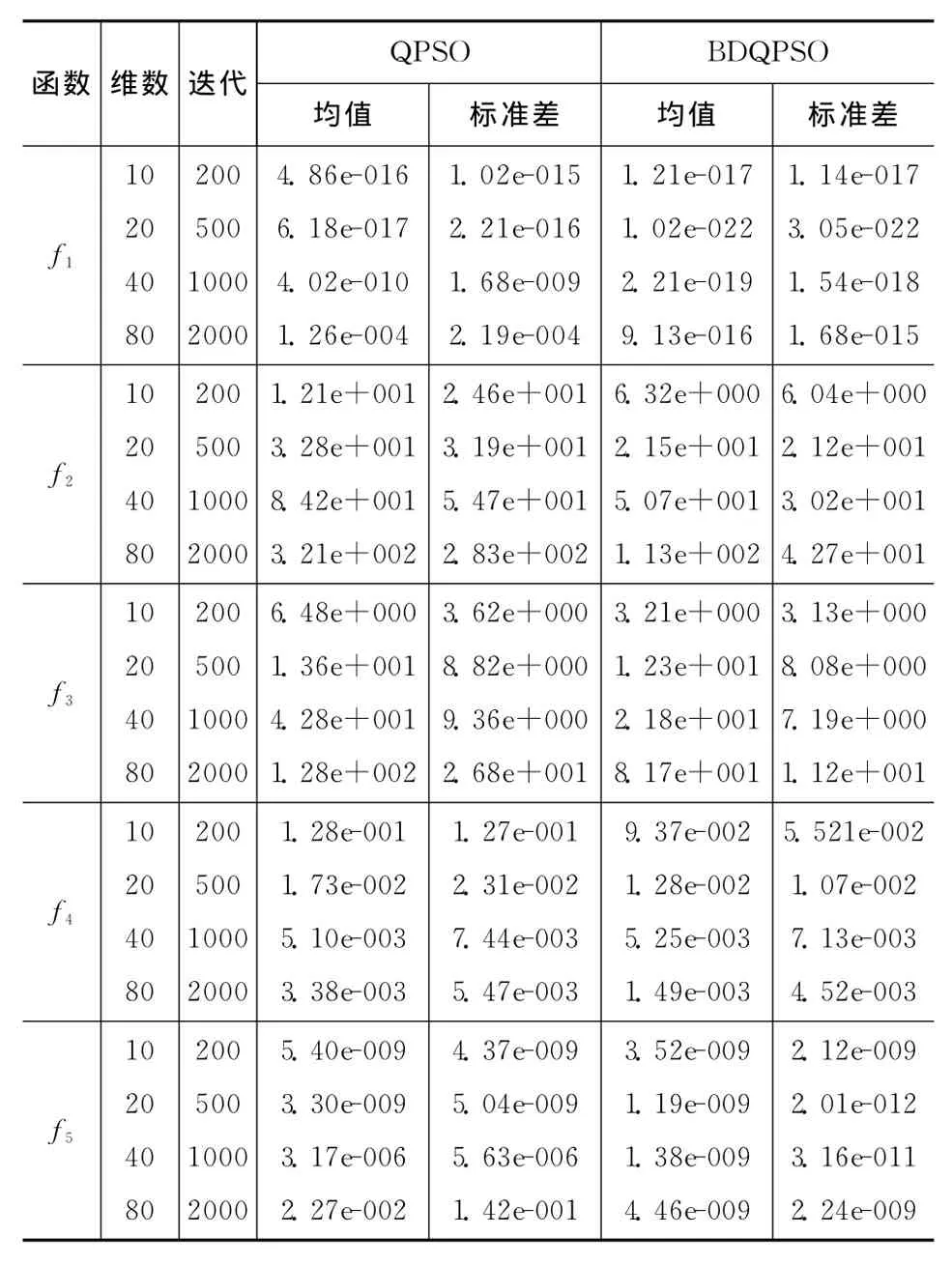
表2 標準測試函數測試結果

對DV－Hop算法的改進分為三部分:第一部分用DV－hop算法計算節點間距離；第二部分用多邊測量法對第一個模塊得到距離計算未知節點的位置坐標；第三部分用BDQPSO算法對第二個模塊得到的位置坐標進行迭代優化。改進的DV－Hop算法的步驟如下:

步驟1 每個信標節點將位置信息包 （節點ID、位置坐標 （xi，yi）和跳數hi）進行廣播，以獲得其它所有錨節點的坐標及跳數距離，然后用式 （1）計算出全網平均每跳距離；

步驟2 每個錨節點廣播其計算的平均每跳距離，數據轉發過程中也進行跳數計數，各個節點通過上述信息計算出該節點到各個錨節點的距離；

步驟3 利用多邊測量法計算出未知節點的位置坐標；

步驟4 將步驟3得到的位置坐標設為BDQPSO算法的初始解，然后開始進行適應度值計算和迭代優化，最終得出更好的結果。

2.3 算法性能分析

為了測試算法性能，擬在100×100的標準矩形區域內，隨機布設300個節點，其中30個是錨節點。首先設置節點通信半徑為10，錨節點GPS定位誤差為0，此時網絡的平均連通度為9.0741，網絡的鄰居錨節點平均數目為0.94276。

實驗過程將錨節點比例從1%開始，以2%的增幅增至19%，圖1是原DV－Hop算法、PSO改進算法、QPSO改進算法和BDQPSO改進算法的節點定位誤差比較結果，實驗環境與2.1相同。從圖1中可見，隨著錨節點比例的增加，BDQPSO改進的DV－Hop算法的定位精度不斷提高，定位誤差可以達到10%左右，這一結果優于DV－Hop算法和其他幾種改進算法。由此可見，在上述3個算法中，提出的BDQPSO改進的DV－Hop算法效果最好，性能最穩定。

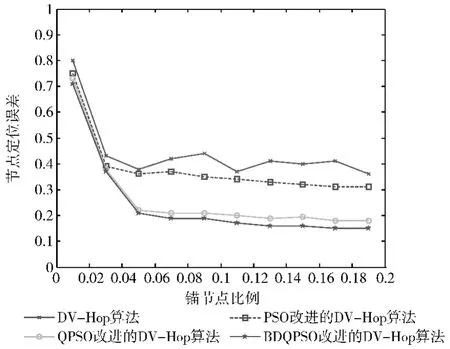
圖1 錨節點比例與節點定位誤差關系

3 改進的移動信標算法

信標節點通過向鄰居節點廣播自身位置使其他節點完成定位，信標節點的比例越大定位精度越高，開銷也越大，為了降低系統開銷需要引入移動信標 （mobile beacon）。

移動信標在待檢測區域 （region of interest，ROI）內以特定的規則移動并向鄰居節點廣播自身位置，未知節點據此計算自身位置，移動方法可采用靜態或動態方法[11]。

由于WSN傳感器節點分布的隨機性，這里提出一種靜態路徑和動態路徑相結合的新方法:首先讓第一個信標以靜態路徑在ROI中進行一遍信號覆蓋，然后讓第二個信標以虛擬力動態路徑[12]進行移動，這樣既發揮了靜態路徑的優勢，又可以靈活地對剩下的節點進行遍歷，提高信號覆蓋率。該方法步驟如下:

步驟1 第一個移動信標參考等距三重優化模型以預先確定好的發射位置移動；

步驟2 應用虛擬力，第二個信標進入ROI進行移動:

（1）第二個信標節點以第一個信標節點的相同位置進入ROI，到達m位置時候向鄰居節點發射位置信息；

（2）在m位置發射半徑內的未知節點收到信息包后，用RSSI算法將損耗功率轉化為距離矩陣；

（3）根據人工勢場理論[13]，第二個信標節點在收到反饋信息后，在m位置計算虛擬力，確定下一個移動位置。

在此過程中有兩種情況需要處理:

1）如果第二個信標節點沒有收到反饋信息或者受到的虛擬力為0，則信標節點向任意方向移動R／2作為新位置；如果連續移動5次以上受到的虛擬力還是0，則跳出程序；

2）如果計算出的第m＋1個發射位置的坐標如果超出了邊界范圍，則坐標回退到第m個位置并向任意方向前進R／4作為第m＋1個發射位置的坐標。

算法的流程圖如圖2所示。

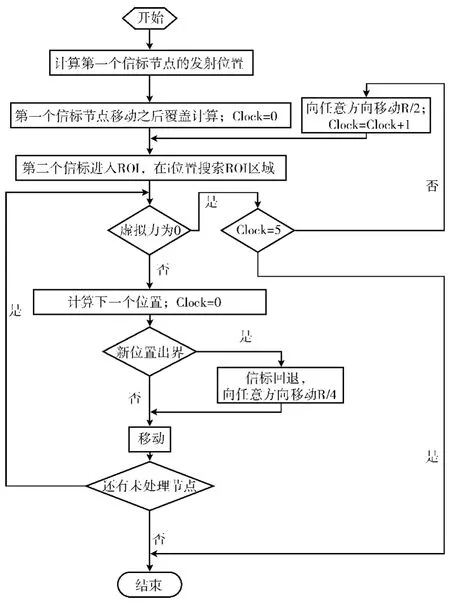
圖2 移動信標算法流程

為了測試算法性能，現在二維空間中進行3組節點定位實驗:

第一組是一個移動信標配有GPS定位裝置，以靜態路徑方式移動；

第二組是一個移動信標配有GPS定位裝置和一個定向天線陣列，按照虛擬力的引導進行動態路徑規劃；

第三組有兩個移動信標，一個用第一組中的靜態路徑移動，另一個用第二組中的動態路徑移動，假定信標的移動速度不變。

實驗條件如下:在100×100的標準矩形區域內，隨機部署50個節點，普通節點發射半徑為10，循環次數都為15次。這3種方法將在信號覆蓋率、發射位置數量以及移動路徑長度方面進行比較。

圖3顯示了3組實驗中沒有被覆蓋的節點數量比較圖，第一組實驗結果較好，未得到3個非共線錨節點信號的未知節點數量較少。第二組和第三組實驗得到的結果差別不太大，但第三組得到的信號未完成覆蓋的節點數相對來說最少。

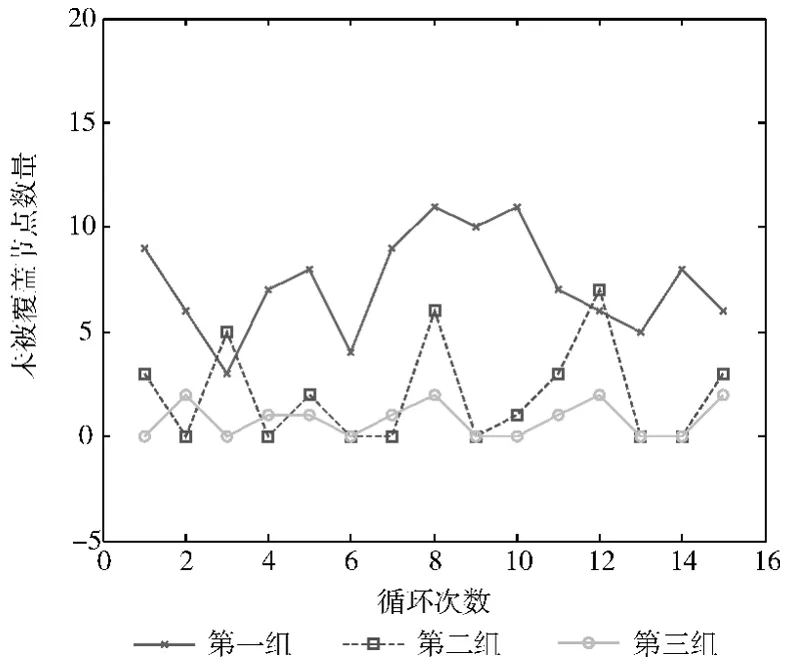
圖3 信號未完全覆蓋節點數量對比

圖4 顯示了發射位置數量的對比圖，只要ROI區域的長度和寬度確定，第一組靜態路徑實驗的發射位置數量就是固定不變的；第三組是第二個移動信標的發射位置數量圖，相對來說發射位置最少，效果最好。

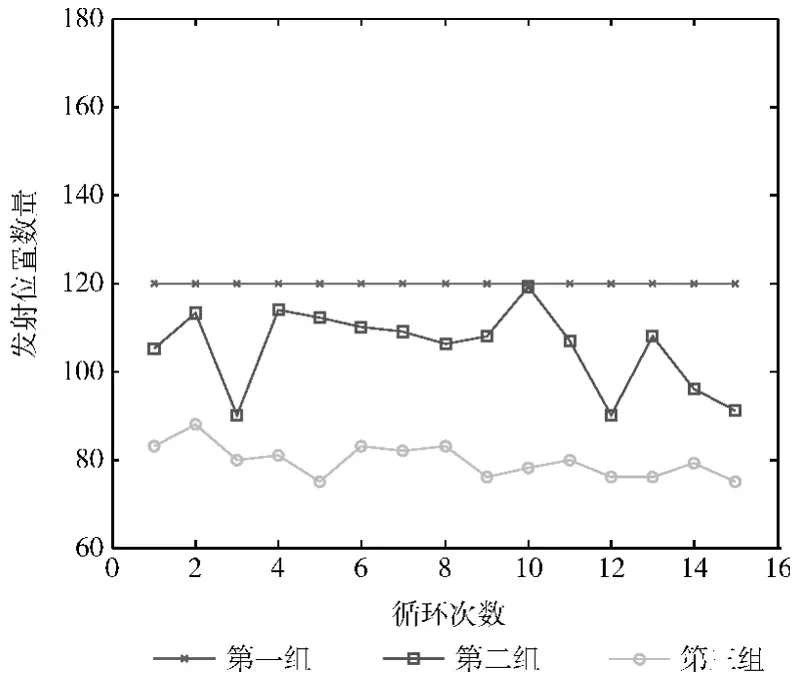
圖4 發射位置數量對比

圖5 是3組實驗中每個信標節點的移動路徑對比圖，從圖中可知，第一組實驗曲線的走勢基本上與圖4中的趨勢一致。第三組實驗也是第二個移動信標的路徑長度，所以該信標的開銷最小，效果也最好。

4 結束語

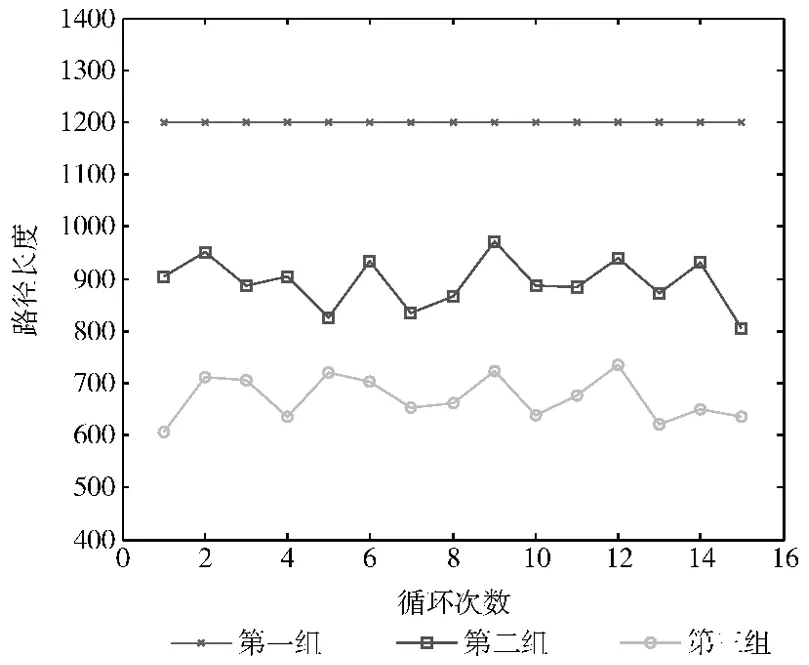
圖5 路徑長度對比

國內外學者對DV－Hop算法提出了許多的改進，大部分都是以降低三邊測量或多邊測量的誤差為出發點，很少有人關注將定位誤差和系統開銷結合起來進行分析。本文不僅用群體智能算法對DV－Hop算法的定位誤差進行改進，同時還用新的移動信標算法降低系統開銷。從實驗結果可見改進的DV－Hop算法提高了節點的定位精度，取得了較好的定位效果；提出的兩個移動信標基于虛擬力的方法，效果比純粹的靜態路徑或者動態路徑具有更好的穩定性、靈活性和信號覆蓋率，降低了系統開銷。雖然增加的移動信標增加了少許系統成本，但換來的是系統定位質量的較大提高，因此具有一定的應用價值和較好的應用前景。

[1]Bartholdy Sanson J，Rodrigues Gomes N，Machado R，et al.Optimization of wireless sensor network using network coding algorithm[C]／／Seville，Spain:The Twelfth International Conference on Networks，2013:21－24.

[2]ZHANG Xinping.A research on localization technique of wireless sensor networks[J].Guangzhou:South China University of Technology，2012（in Chinese）.[張新平.無線傳感器網絡中的定位技術及應用研究[D].廣州:華南理工大學，2012.]

[3]JIAO Binliang，ZHANG Ke.Localization algorithm based on stochastic proximity embedding in wireless sensor networks[J].Journal of Chinese Computer Systems，2013，34 （2）:269－271（in Chinese）.[焦斌亮，張可.基于SPE的無線傳感器網絡定位算法[J].小型微型計算機系統，2013，34（2）:269－271.]

[4]Li Wenwen，Zhou Wuneng.Genetic algorithm－base localization algorithm for wireless sensor networks[C]／／Seventh International Conference on Natural computation，2011:2096－2099.

[5]CHEN Xingzhou，LIAO Minghong，LIN Jianhua.Improvement of node localization in wireless sensor network based on particle swarm optimization[J].Journal of Computer Applications，2010，30 （7）:1736－1738（in Chinese）.[陳星舟，廖明宏，林建華.基于粒子群優化的無線傳感器網絡節點定位改進[J].計算機應用，2010，30 （7）:1736－1738.]

[6]Zhao J，Fu Y，Wang H B.Localization technology based on quantum－behaved particle swarm optimization algorithm for wireless sensor network[J].Applied Mechanics and Materials，2012，220:1852－1856.

[7]Yu C B，Yu L，Tan J，et al.DV－Hop localization algorithm in wsn based on weighted of correction in hop distance[J].Applied Mechanics and Materials，2013，303:143－148.

[8]Luo X，Liu Y，Long C，et al.Range－free localization algorithms in wireless sensor networks[C]／／Fifth International Conference on Machine Vision Algorithms，Pattern Recognition，and Basic Technologies，2013:42－49.

[9]FU Tao.Study on the hybrid localization algorithm of wireless sensor networks[D].Lanzhou:Lanzhou University，2012（in Chinese）.[傅濤.無線傳感器網絡混合定位算法研究[D].蘭州:蘭州大學，2012.]

[10]SUN Jun，WU Xiaojun，FANG Wei，et al.Quantum－behaved particle swarm optimization:Theory and application[M].Beijing:Tsinghua University Press，2011 （in Chinese）.[孫俊，吳小俊，方偉，等.量子行為粒子群優化:原理及其應用[M].北京:清華大學出版社，2011.]

[11]Zhou W，Shi W，Gao P，et al.Localization using a mobile beacon in wireless sensor networks[J].Information Technology Journal，2013 （12）:323－330.

[12]LI Shijian，XU Congfu，YANG Yang，et al.Getting mobile beacon path for sensor localization[J].Journal of Software，2008，19 （2）:455－467（in Chinese）.[李石堅，徐從富，楊旸，等.面向傳感器節點定位的移動信標路徑獲取[J].軟件學報，2008，19 （2）:455－467.]

[13]JIA Qingxuan，ZHANG Qianru，GAO Xin，et al.Dynamic obstacle avoidance algorithm for redundant robots with pre－selected minimum distance index[J].Robot，2013，35 （1）:17－22（in Chinese）.[賈慶軒，張倩茹，高欣，等.預選擇最小距離指標的冗余機器人動態避障算法[J].機器人，2013，35 （1）:17－22.]