軟件測試用例執行優化研究

王吉茂，尹 平，張慧穎

（北京跟蹤與通信技術研究所，北京100094）

0 引 言

測試用例執行優化的研究內容主要分兩方面:一是在一組測試用例執行前調整測試用例的執行順序；二是在測試用例執行過程中動態調整未執行測試用例的順序。執行前調整測試用例的執行順序是為了達到一定的測試性能指標，目前測試領域研究的測試性能指標主要包括需求的覆蓋能力、代碼的覆蓋能力、錯誤探測能力、已發現錯誤的等級、測試耗費等，然而卻缺少對多個測試用例的執行條件和期望結果之間聯系的研究，導致測試執行時冗余操作增多；另外，按照測試理論的Pareto原則，80%的軟件問題很可能集中在20%的程序模塊中，在測試過程中提前執行與存在缺陷的軟件模塊相關的測試用例能夠更加全面、集中地暴露軟件問題，但目前缺少度量測試用例之間聯系的方法以及基于這種度量的動態調整算法。因此，本文從測試用例執行條件和期望結果的關系入手設計了測試用例執行前優化算法，定義了測試用例距離的概念和計算方法并基于測試用例距離設計了執行中動態調整算法。

1 相關概念及工作

測試用例的執行優化是對已有測試用例按照某種特定的順序執行，從而達到某些性能指標的調度過程[1]，其具體的定義為[2]:對于某些測試套T，PT表示對T中元素所有可能的排列的集合；f表示應用于PT中每種排序的評價函數，輸出的是每種排序的判定值，值越高效果越好。測試用例執行優化就是尋找一個T＇∈PT，使得對于任意T＇∈PT，都有f（T＇）≥f（T＇）。

1.1 測試用例執行前的優化算法概述

Rothermel等研究人員首先將測試用例集按照對代碼的覆蓋能力進行排序[3]，然后分別使用排序前后的測試用例進行實際測試，對比測試效果，實驗結果證明為測試用例設置優先級并排序能夠提高測試中錯誤檢測的速度和效率[4]。

在考慮代碼覆蓋能力方面，最著名的是基于MC／DC（modified condition／decision coverage）覆蓋準則的排序研究。關于MC／DC的定義及基于MC／DC提出的測試用例優先級算法可以參見文獻[5]。

對于該方法，Elbaum等認為其只考慮了覆蓋因素和出現頻率，而忽略了工程實踐中的測試耗費問題[6]。在這個基礎上，他們提出了綜合考慮測試耗費和錯誤嚴重程度的測試用例優先級排序方法[7]，在之前覆蓋率標準上增加了對測試開銷的考慮，優先級比較的標準改為單位覆蓋消耗比率，同時結合錯誤嚴重程度重新評估測試用例的潛在探錯能力。

測試用例執行前的排序還可以依據其錯誤探測能力來排序，可以將錯誤探測能力定義為發現錯誤的數量。采用基本貪心算法將測試用例按照錯誤探測能力從大到小排序，然后依次執行直到所有的錯誤都被探測出來。額外貪心算法則是在每次取用測試用例的時候，根據剩下的未被探測出來的錯誤動態更新測試用例的探錯能力，再采用貪心策略選用測試用例。之所以要設計額外貪心策略，是由于基本貪心策略會選擇到不必要的測試用例，但額外貪心策略容易陷入局部最優。

依據錯誤探測能力，還可以利用啟發式方法來對測試用例進行排序。較典型的有爬山算法。作為深度優先搜索的一種改進，爬山算法利用反饋信息幫助生成解的決策，是一種局部搜索算法。該算法的優點在于不必進行遍歷，通過只選擇部分節點來提高效率，缺點在于不能全局搜索，容易陷入局部最優。

北京系統工程研究所的楊廣華、包陽等人研究了基于需求的測試用例優先級排序算法，包括對首次測試和回歸測試的測試用例的優先級排序。

首次測試的優先級排序可以分為根據需求的優先級RP（requirement priority）排序、需求變更情況RM （requirement modify）排序、實現復雜度 （implementation complexity）排序。其中根據需求的優先級排序是由于按這種方式排序可以提高測試的效益，因為據統計，用戶經常使用的軟件功能只占該軟件所有功能的40%左右；按照需求變更情況來排序是由于需求的變更是引入軟件缺陷的一個重要原因，而在軟件完成之前平均有25%的需求會發生變更；另外，復雜程度較高的軟件模塊通常存在較多的缺陷，因此重點測試復雜程度較高的軟件模塊能提高發現軟件缺陷的效率。

回歸測試用例優先級排序考慮之前測試發現軟件缺陷的情況，根據檢測到不同缺陷嚴重性等級對測試用例的錯誤探測能力進行賦值，然后根據賦值情況提高缺陷探測能力較高的測試用例的優先級。

1.2 測試用例執行中的優化算法概述

除了可以在測試用例執行之前對其進行優化排序，還可以在測試用例執行中對未執行測試用例的執行順序進行動態調整，以達到在短時間內高效測試的目的。

戴如昕、顧春華研究了通過調整測試用例的執行順序的測試用例優先級方法[8]。這種方法首先根據測試用例可能暴露的錯誤類型建立一個關系矩陣R。根據矩陣R，測試用例被其可能暴露的錯誤類型分成不同的組，然后該方法調用Escalate（提高算法）和Deescalate（降低算法）來調整用例的優先級。在這兩種算法中都有一個輸入參數a來確定優先級的調整幅度。在實際執行中，如果某個測試用例暴露了軟件問題，說明軟件在這方面存在隱患，提前執行同組的同類型測試用例，從而有助于更高效地發現此問題的各個方面。

在測試用例執行過程中，根據實時反饋的信息 （主要是未完成的測試目的或未覆蓋的測試需求），將剩余的測試用例不斷地進行順序調整。當返回多個反饋信息時，這種調整還可以不是單隊列的，而是在并行的情況下進行多個測試用例隊列同時調整[9]。并行調整可以增加調整系統對反饋信息的容納能力，避免了單隊列出現反復調整的情況，但多隊列增加了算法的復雜度。

2 測試路徑控制陣列

為了能夠兼顧測試用例執行前和執行中的優化算法，本文首先提出測試用例的組織模型:測試路徑控制陣列（test path control array，TPCA）。下面對該模型進行說明

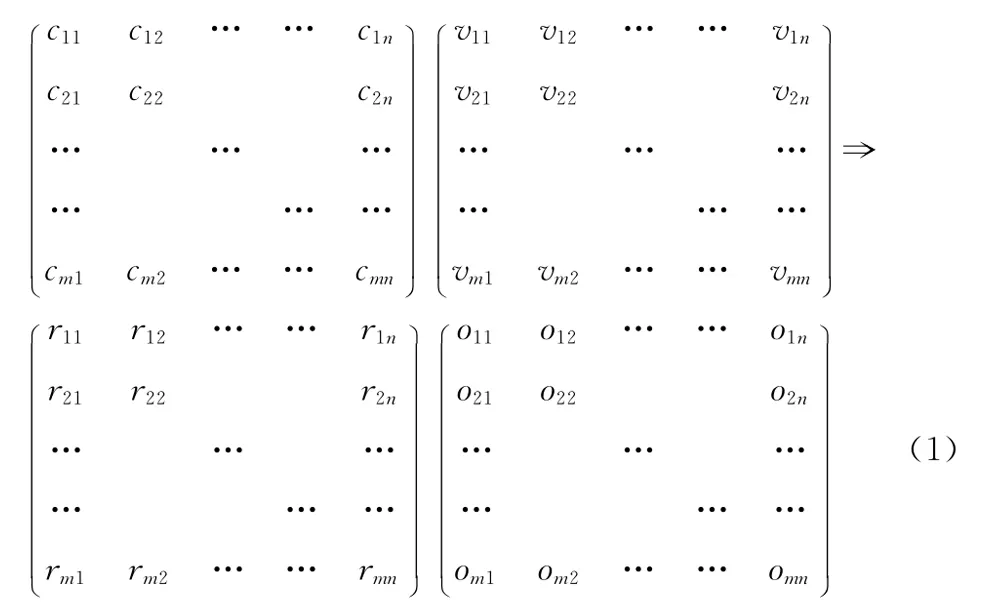
式 （1）可簡寫為

C、V、R、O均是m×n的陣列 （并非矩陣），表示針對同一個被測功能項的m個測試用例的數據。

C為輸入控制陣列，其每一行表示一個測試用例的輸入控制量，輸入可以包括軟件當前狀態、將要發生的事件和參數取值。C中的元素cij表示第i個測試用例的第j個輸入控制量，取值為0或1。cij取值為0表示V中的輸入vij狀態值無效、事件不發生或參數取值無效，取值為1表示V中的輸入vij狀態值有效、事件發生或參數取值有效。

V為輸入陣列，其每一行表示一個測試用例的輸入值，每個測試用例最多有n個輸入值。vij可以表示一個狀態值、事件 （0為不發生、1為發生）、輸入參數的具體取值。

R為期望結果控制陣列 （或輸出控制陣列），其每一行表示一個測試用例的輸出控制量，輸出可以包括測試用例執行后軟件預期狀態、預期發生的事件和參數取值。R中的元素rij表示第i個測試用例的第j個輸出控制量，取值為0或1。rij取值為0表示O中的輸出oij狀態值無效、事件不發生或參數值無效，取值為1表示O中的輸出oij狀態值有效、事件發生或參數取值有效。

O為輸出陣列，其每一行表示一個測試用例的輸出值，每個測試用例最多有n個輸出值。當R中的rij＝1且rij表示輸出參數控制量時，oij為第i個測試用例的第j個輸出參數的取值。vij可以表示一個狀態值、事件 （0為不發生、1為發生）、輸出參數的具體取值。

3 測試用例執行前優化算法

3.1 算法說明

在執行一個測試用例前通常要對軟件的運行環境、狀態、參數等進行初始化設置，而測試用例執行結束后會產生執行結果。兩個測試用例，其輸入條件和輸出結果之間可能存在下面定義的情況。

定義1 設A、B為兩個測試用例，A.Conditions表示A執行前的輸入條件，A.Results表示A執行后的輸出和軟件狀 態的變化，B同理。若存在｛A.Results｝∩｛B.Conditions｝≠ ，則稱為創造場景條件｛A.Results｝∩｛B.Conditions｝而進行的操作為重復操作。

定義2 N｛A.Results｝∩｛B.Conditions｝為執行測試用例B所需的輸入條件中，測試用例A在執行后能為其產生的、測試人員無須進行重復輸入的操作步驟數，稱為操作重復度。

操作重復度定量描述了測試用例之間的聯系。操作重復度不為零的兩個測試用例在執行順序上應該被安排在相鄰的位置。尤其是針對運行狀態眾多，各狀態轉換關系復雜的軟件，需要設計一種算法來尋找操作重復度之和最大的測試用例執行順序，該問題建模如下:

設X＝｛Xi｜i＝1……n｝是測試用例的集合，且對于任意測試用例Xi、Xj，二者之間的操作重復度N｛Xi.Results｝∩｛Xj.Conditions｝已知，求 X中測試用例的一個排序，該排序滿足操作重復度之和最大，即

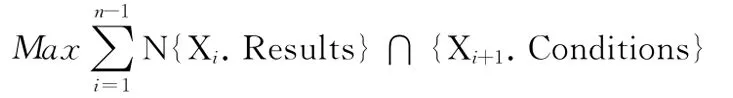
這個排序問題可以轉化為圖論中尋找帶權有向圖G（X，E）遍歷所有節點的最大路徑問題，其中X中的測試用例是有向圖中的節點，E是權值為N｛Xi.Results｝∩｛Xj.Conditions｝的邊的集合。如果某個測試用例執行條件或期望結果與其他測試用例沒有聯系，則設其對應邊權值為0，但仍認為該邊存在。因此G （X，E）可以視為一個有向完全圖。

圖論中解決有向圖節點排序 （即有向圖活動規劃）的方法有AOV網絡和AOE網絡。但AOV網絡的活動在節點上，拓撲排序僅能確定圖中是否有環，不涉及邊權值的問題；AOE網絡的活動在邊上，可以求解出活動節點的關鍵路徑，但并不能做到對節點的完全覆蓋[10]。因此兩種算法都不適用于測試用例排序。

雖然目前沒有現成的解法適用于這個問題。但實際測試中，一個測試用例執行完成只對其他測試用例特定輸入條 件 提 供 便 利。例 如，A.Conditions＝｛a，b，c｝，B.Results＝｛b，c｝，C.Results＝｛c｝，當B執行后，執行測試用例A只需要創造條件a即可，此時再執行C不會給A提供任何便利。這說明一個測試用例執行后就會給其他測試用例帶來影響，而且影響具體到某一個特定的軟件狀態，而不僅僅是狀態數量的概念。

因此，從減少操作步驟這個目的出發，以貪心策略為指導思想，借鑒AOV網絡拓撲排序中逐個取節點的方法，設計出如下有向圖節點排序算法:

首先定義數據結構

節點 （代表測試用例）:

算法流程如圖1所示。

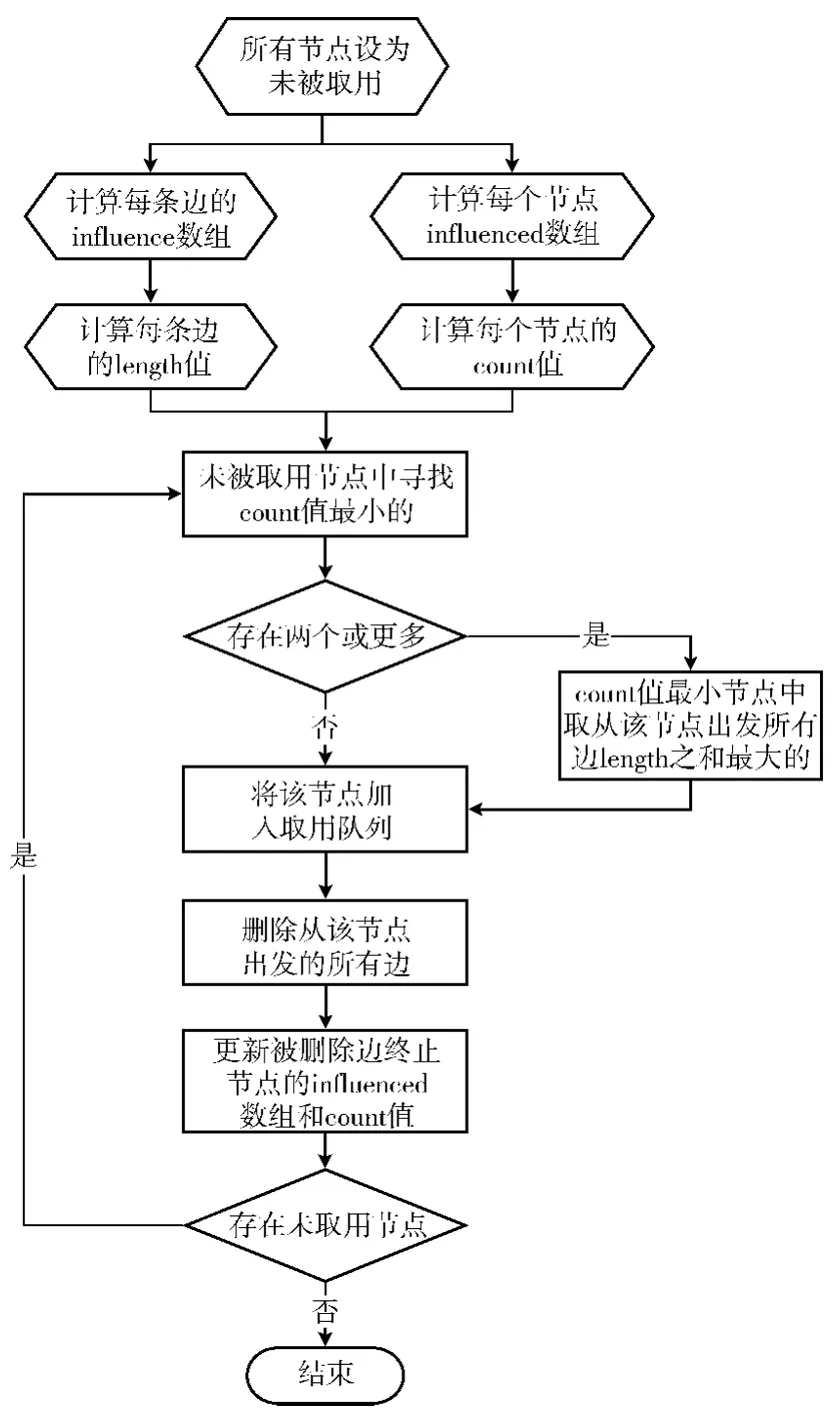
圖1 測試用例執行前優化算法

3.2 應用驗證

以航天測控系統實時系統軟件主副機切換功能的32個測試用例為優化排序的對象。

在經3.1節算法優化前，測試用例按照編號從小到大的順序執行。經3.1節優化后，測試用例執行順序為4、16、2、8、14、0、18、24、30、19、25、31、3、9、15、1、7、13、17、23、29、5、11、21、27、10、6、20、12、26、22、28。優化排序使當前測試用例期望結果中軟件的狀態與下一個測試用例執行所需的輸入條件十分接近，冗余操作明顯減少。

在假設32個測試用例全部執行通過的情況下，本文統計了所有測試用例的總步驟數、測試用例按0到31順序執行省去的步驟數以及經優化排序后省去的步驟數，優化效果見表1。

表1 優化效果

4 測試用例執行中動態調整算法

4.1 算法說明

本算法基于測試用例距離，因此首先給出測試用例距離的定義，用以衡量測試用例的相似程度。

定義3 測試用例距離dij

其中，λk表示第k個參數賦值的權重系數，視測試結果對該輸入的敏感程度由測試人員來確定。沒有賦值操作或者該參數值對測試結果沒有影響的測試用例，該值為0。

cij和vij來源于測試路徑控制陣列中的C陣列和V陣列；v＇ij是通過對輸入參數vij歸一化得到的，歸一化方法為:由于輸入參數vij的取值范圍可以被劃分成若干個等價類，一個等價類的數值范圍可能很大，例如，如果在等價類[1，10000]中vij＝2或vij＝9999時軟件的執行結果沒有差異，則定義當vij取值來自于同一個有效類的時候，v＇ij取值為同一個正整數q；同理，當vij取值來自于同一個無效類的時候，v＇ij取值為同一個負整數p；當vij取值為邊界值時，v＇ij取值為0。

當測試用例i檢測到軟件問題時，定義測試用例i為目標測試用例。給定測試用例距離d，如果dij＜d，則認為測試用例j與i屬于相關測試用例，測試用例j應被提前執行。d通常由經驗值給出。

對于一個給定的d，可能存在多個測試用例與目標測試用例是相關測試用例，但這些測試用例與目標測試用例的測試用例距離可能不同。相關性較強的測試用例應當優先執行，即按照測試用例距離遞增的順序調整，其具體實現流程如圖2所示。

4.2 應用驗證

這里仍以實時系統軟件的主副機切換功能的測試用例來驗證上節的算法對測試用例執行順序的動態調整效果。

在API請求切換程序模塊中設置一個軟件缺陷，使API請求不能成功切換主副機。與缺陷有關的測試用例集合為｛0，2，4，6，8，16，18，20，22｝。

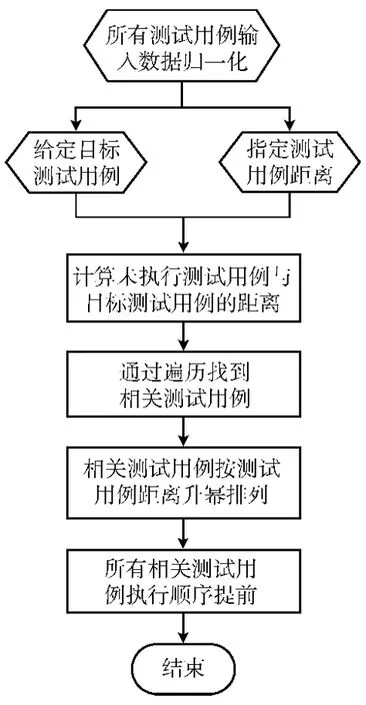
圖2 基于距離的動態調整算法流程

按照3.2節優化后的測試用例執行順序執行32個測試用例。在執行測試用例4時，該測試用例不通過，現象為:在自動模式、主副機均運行的情況下，被測軟件不能實現通過API請求將運行機從主機切換到副機。

用基于測試用例距離的動態調整算法對未執行測試用例排序。現在，目標測試用例為測試用例4，按照式 （3）給定測試用例距離閾值d＝1.8，自動模式、API請求的權重為3，其他輸入的權重為0.25，通過程序尋找與目標測試用例的測試用例距離小于1.8的測試用例。

算法程序找到了10個測試用例｛4，8，6，0，2，20，24，22，16，18｝，雖然多出一個測試用例24，但包含了與缺陷相關的測試用例，并且優化算法把與缺陷相關的測試用例6、20、22提前到前10位執行。

5 結束語

本文在研究現有的測試用例執行優化方法的基礎上，首先提出測試路徑控制陣列模型來組織測試用例；然后從圖論角度出發提出測試用例執行前的優化排序算法；最后提出了測試用例距離的概念和計算方法，并基于測試用例距離提出測試用例執行中動態調整算法。將以上兩個算法應用于實時系統軟件主副機切換功能的測試用例中，優化結果表明，執行前優化排序算法能夠減少一組測試用例的冗余操作，執行中動態調整算法能夠找到與軟件缺陷相關的測試用例并將其執行順序提前。

[1]JIANG Shanshan，ZHAO Zhonghua，WANG Qiming，et al.A requirement－based approach to system－level black－box test case prioritization[J].Computer and Digital Engineering，2010，38（5）:68－73 （in Chinese）.[姜姍姍，趙中華，王啟明，等.基于需求的系統級黑盒測試用例優先化方法[J].計算機與數字工程，2010，38 （5）:68－73.]

[2]Moisiadis F.Prioritizing test cases and scenarios[C]／／37th International Conference on Technology of OO Languages and Systems，2000:108－119.

[3]Wong We，Horgan JR，London S，et al.A study of effective regression testing in practice[C]／／Proceedings of the 8th IEEE International Symposium on Software Reliability Engineering.Washington IEEE Computer Society，1997:264－274.

[4]Rothermel G，Untch H R，Chu C，et al.Test case prioritization:An empirical study[C]／／Proceedings of the International Conference on Software Maintnance.Washington:IEEE Computer Society，2001:179－188.

[5]LU Dezhong.Research for modified condition／design test case priorty algorithm[J].Science and Engineer，2009，9 （14）:4040－4044 （in Chinese）.[盧德忠.基于 MC／DC的測試用例優先級 算 法 研 究[J].科 學 技 術 與 工 程，2009，9 （14）:4040－4044.]

[6]Elbaum S，Malishevsky G，Rothermel G.Incorporating varying test costs and faults verities into test case prioritization[C]／／Proceedings of the International Conference on Software Engineering，2001:329－338.

[7]QU Bo，NIE Changhai，XU Baowen.Survey of test case priori tization for regression testing[J].Journal of Frontiers of Computer Science and Technology，2009，3 （1）:225－233 （in Chinese）.[屈波，聶長海，徐寶文.回歸測試中測試用例優先級技術綜述[J].計算機科學與探索，2009，3 （1）:225－233.]

[8]DAI Ruxin，GU Chunhua.Advanced test case prioritization for black box testing[J].Computer Engineering and Design，2010，31 （20）:4343－4346 （in Chinese）.[戴如昕，顧春華.用于黑盒測試的測試用例優先級改進算法[J].計算機工程與設計，2010，31 （20）:4343－4346.]

[9]QU Bo，XU Baowen，NIE Changhai.A dynamic prioritization method for supplemental test cases[J].Journal of Shandong University，2009，39 （2）:137－140 （in Chinese）.[屈波，徐寶文，聶長海.補充生成測試用例的優先級設定與動態調整算法[J].山東大學學報，2009，39 （2）:137－140.]

[10]WANG Guiping，WANG Yan，REN Jiachen.Algorithm，implementation and application of graph theories[M].Beijing:Press of Peking University，2011:63－82 （in Chinese）.[王桂平，王衍，任嘉辰.圖論算法理論、實現及應用[M].北京:北京大學出版社，2011:63－82.]