基于快速傅里葉變換的遙測信號載波估計算法

馮 欣，唐曉峰，孫發魚，李建立

（1.機電動態控制重點實驗室，陜西 西安 710065；2.西安機電信息技術研究所，陜西 西安 710065）

0 引言

近年來，隨著數字信號處理（Digital Signal Processing，DSP）及軟件技術的不斷發展，傳統的遙測技術也不可避免地逐漸向軟件化平臺轉變。在軟件環境下，對比傳統遙測系統中的非相干解調，相干解調的優勢大大體現出來。而相干解調帶來一個很重要的問題，就是信號的同步問題［1］。

在目前的遙測體制下，遙測信號往往會出現較大的載波頻偏。特別地，在遙測系統設計測試階段，信號載波頻偏甚至可達數兆赫茲。在這種情況下，傳統鎖相環路由于受環路捕獲帶寬的限制，無法實現快速同步［2］。因此，需要在鎖相環前加入對載波頻率的估計的環節。目前廣泛使用的基于參數模型的譜估計方法，由于運算復雜度較高，并不適用于實時接收的遙測系統。而目前基于離散傅里葉變換（Discrete Fourier Transform，DFT）的頻譜估計算法，主 要 應 用 于 相 移 鍵 控 （Phase Shift Keying，PSK）等信號［3］，并不能直接適用于以脈沖編碼調制（Pulse Code Modulation，PCM）的遙測信號。本文針對此問題，提出了基于快速傅里葉變換的遙測信號載波估計算法。

1 頻譜估計及PCM信號原理

1.1 基于DFT的載波頻譜估計原理

設載波的解析信號離散采樣序列為：

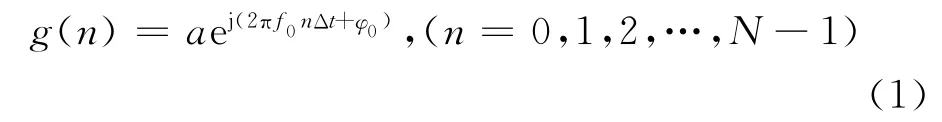
其中a，f0，φ0分別表示信號的振幅、頻率、初相，Δt表示信號采樣時間間隔。

其DFT（所得多項式）系數為

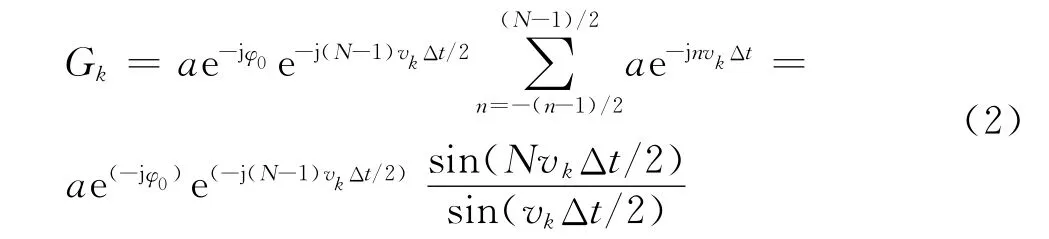
其中

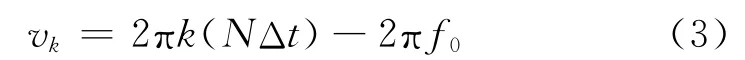
由式（2）、（3）可知，vk中包含了f0的信息。因此，對原信號進行DFT后，搜索出最大譜線，其對應的頻率，便是載波頻率的估計值。

可見，基于DFT的直接頻譜估計方法，物理意義明確，且借助快速傅里葉變換（Fast Fourier Transform，FFT）后計算量也相對較小。因而可廣泛應用于工程實踐中。但DFT中存在能量泄漏和柵欄效應［4］，且在算法精度上依賴于采樣率及采樣長度，也使得該方法具有很大的限制。

1.2 信號頻譜細化算法［4］

設采樣頻率為fs，信號x（t）經采樣后得到離散信號x（n），則其DFT可表示為：

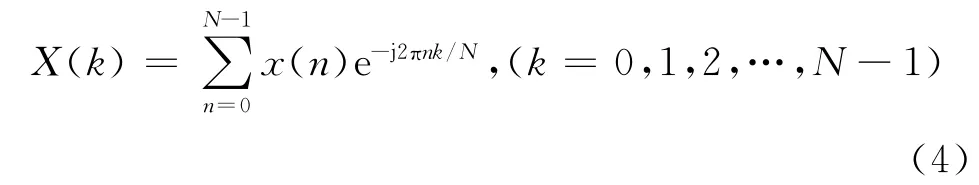
其頻譜分辨率為Δf＝fs／N，即存在量化誤差。若要降低量化誤差，必須降低采樣率fs或提高點數N。然而采樣率受乃奎斯特采樣定律限制；而提高采樣點數N則會大大增加數據處理量，不僅會增加硬件成本，而且會影響信號處理的實時性。因此亟待研究信號頻譜算法，使得在數據處理量不變或增加相對較低的情況下，提高頻譜分辨率，降低量化誤差。

由DFT的導出可以看出，其實質是對原信號頻譜一個周期的采樣。若對原信號平移1／2倍量化頻率后，再進行DFT后得到的頻譜，正好是對原信號DFT的插值。如圖1所示。若將兩組信號DFT的結果合并起來，其頻譜分辨率會比原信號DFT的結果提高一倍。

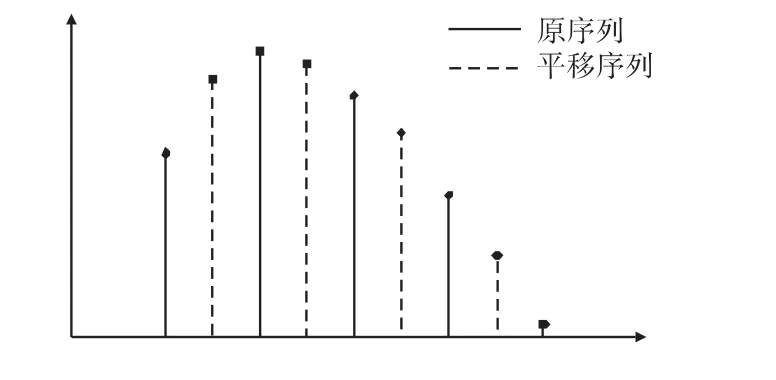
圖1 原序列與平移序列Fig.1 The original sequence and Thetranslational sequence

同理，若分別對信號平移1／m、2／m、…、（m －1）／m倍量化頻率后，在分別進行DFT并將結果進行合并，其頻譜分辨率將為原信號DFT的1／m倍。

應用FFT算法，該頻譜算法可表示為：

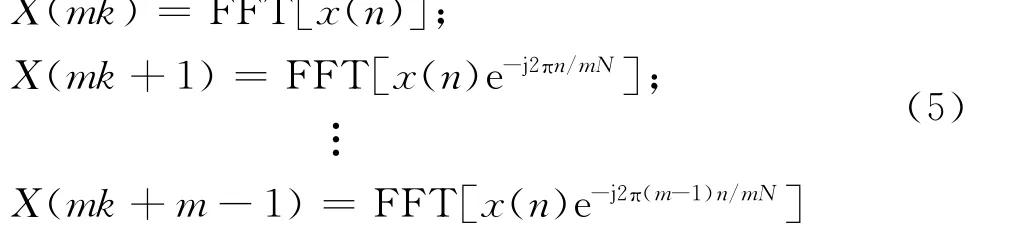
其中FFT［x（n）］表示對x（n）的快速傅里葉變換。

對于N點的FFT算法，總共需要（Nlog2N）／2次復數乘法運及Nlog2N 次復數加法運算［5］。可見，該頻譜算法的復數乘法運算量和復數加法運算量僅為同樣頻譜分辨率的FFT算法的50%。

1.3 PCM信號頻譜特點

對于PCM調制信號，其數學表達式為

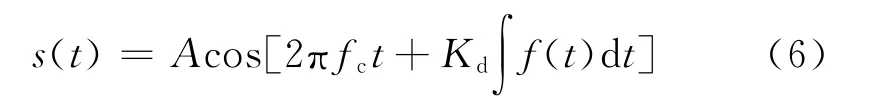
其中：A為載波幅度，fc為載波頻率，f（t）為調制信號，Kd為頻偏常數。若碼速率為Rb，對于不歸零碼，碼元“0”和“1”對應的載波頻率分別為：

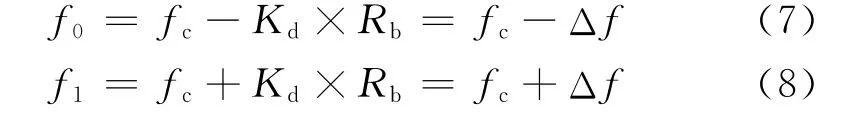
Δf又稱為調制頻偏。對于PCM數字信號，存在一個最佳的調制頻偏，位于：

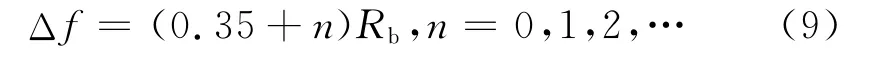
式（9）中n越大，誤碼率越小，但需要的信道帶寬也越大，因此一般情況取n＝0［6］。

以中頻載波信號頻率＝70MHz，碼速率＝2 Mbps為例，PCM調制信號頻譜如圖2所示。

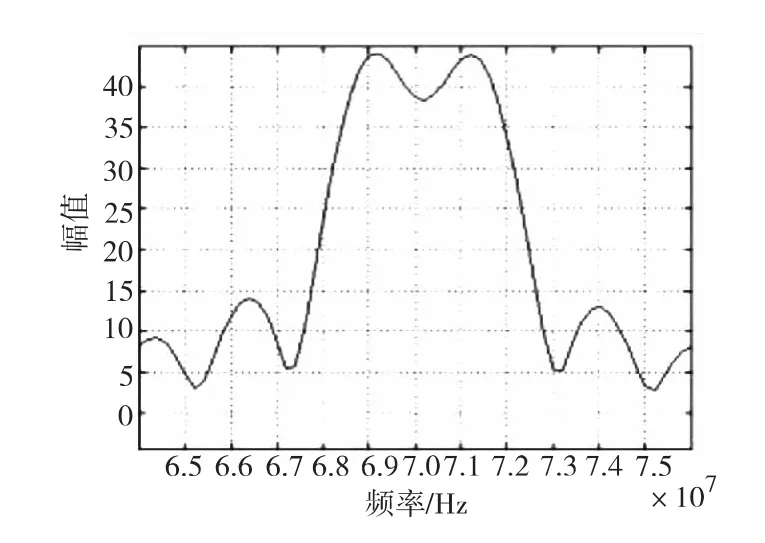
圖2 PCM調頻信號頻譜示意圖Fig.2 PCM－FM signal spectrum diagram

2 針對PCM遙測信號的載波估計算法

對于PCM調制體系的遙測信號，由于其頻譜為雙峰，基于DFT的頻譜算法顯然不能直接適用。但注意到PCM遙測信號的頻譜實際相當于兩個單音信號頻譜的疊加。這兩個信號的載波頻率分別為f0和f1。對式（8）進行移項，并帶入式（7），可得

因此，只要分別估計出兩個單音信號的載波頻率，就可得到PCM遙測信號的載波估計。結合頻譜算法后，可以進一步減少算法計算量，提高估計算法的實時性。

而對PCM遙測信號的載波估計主要應用于同步鎖相環節，以協助完成載波快速同步。對于頻譜算法，由于等式（11）的成立。

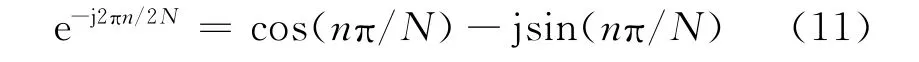
非常類似常用同步鎖相環節同相正交環（Costas環）中的同相及正交環節。因此，該算法可以很方便地作為外環嵌入鎖相環中，其原理框圖如圖3所示。

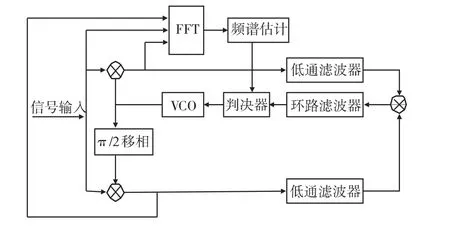
圖3 頻譜算法嵌入Costas環原理框圖Fig.3 The spectrum algorithm embedded in Costas loop block diagram

具體算法實現過程如下：

1）采樣：在中頻端對信號進行采樣，并應用式（5）的頻譜細化算法，令m＝2進行一倍插值，得到信號的頻譜序列 Gk2。

2）頻譜排序：對序列 Gk2進行搜索，搜索出20個最大值，并按由大到小順序進行排列，得到新的序列Zkik，其中ki為與Zkik相對應的原序列的頻譜號。

3）頻譜分組：令k0＝ ［max（ki）＋min（ki）］／2，以k0為基準，對Zkik進行分組，第一組ki≤k0，第二組ki＞k0。

4）頻譜搜索：找出各組最大值，分別記作Z1和Z2，Z1和Z2即為PCM的兩個單載頻信號頻譜的最大值。

5）頻譜計算：對Z1和Z2在序列 Gk2中的對應序列，乘以頻譜分辨率，分別得到兩個單載頻的估計值f0和f1，帶入式（10），即可得到PCM信號的載波頻率估計值。

3 仿真分析

在Matlab仿真平臺上對該算法進行建模。設PCM遙測信號中頻載波頻率為（70±5）MHz，碼元速率為2Mbps，調制頻偏為0.7MHz。設采樣率為200MHz，采樣點數為1024點，則理論頻譜分辨率約為200kHz。應用頻譜算法后，頻譜分辨率應提高至100kHz，即估計出的載波頻率與實際載波頻率誤差應在±50kHz之間。一般來說，在測試系統中，信號信噪比一般會大于0dB，為更全面驗證算法的有效性，分別對信噪比為－4dB到10dB的信號進行仿真分析。

圖4給出了在不同信噪比下對載波頻率估計的誤差的仿真結果。

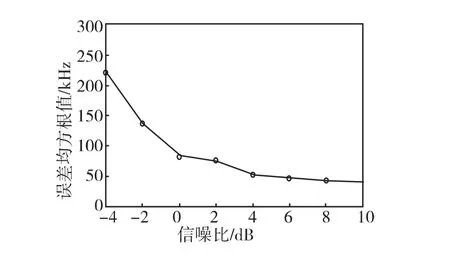
圖4 不同信噪比下估計誤差仿真結果Fig.4 Simulation result of estimation error on different SNR

從圖4可以看出，在信噪比較高（大于－2dB）的情況下，該算法估計誤差較小，基本在150kHz以內，估計誤差小于3%，略高于無噪聲干擾的理論值；隨著信噪比的提高，估計性能也隨之提升。當信噪比大于4dB的時候，頻率估計誤差基本穩定在50kHz以內，估計誤差小于1%，和無噪聲的理論值吻合。而對于一般鎖相環路，其環路捕捉帶寬均可設計達到300kHz左右［7］。因此，該估計算法完全可以滿足鎖相環環路捕獲帶寬的要求，從而達到協助鎖相環完成快速同步目的。

而在實際應用中，該算法可以通過一個判決環節（如框圖3中的判決器）進行控制。使得只有當鎖相環節出現失鎖時，才控制該算法進行工作；未出現失鎖時，該算法處于屏蔽狀態。這樣一來，更好地節省了系統的資源。

表1具體給出了信噪比分別等于－2dB、0dB、2dB、4dB時的仿真結果。

表1 SNR＝－2dB、0dB、2dB、4dB時的仿真結果Tab.1 Simulation result when SNR＝－2dB，0dB，2dB，4dB MHz

4 結論

本文提出了基于FFT的PCM遙測信號頻譜估計算法。該算法針對PCM遙測信號頻譜呈現雙峰的特點，以FFT算法原理為基礎，結合頻移技術，實現了針對常規兵器遙測調制信號的實時載波頻譜估計。同時，該算法還可作為同相正交環的外環嵌入到鎖相環節中，以協助鎖相環完成載波信號快速同步。仿真結果表明，該算法在信噪比較高的情況下，估計誤差基本穩定在50kHz以內，完全滿足鎖相環環路捕獲帶寬的要求，以達到快速同步的目的；同時，該算法具有實現簡單、實時性強、頻譜估計范圍寬等優點，有較強的工程實用性。但在低信噪比的情況下，如何提高估計精度，需要進行進一步的研究。

［1］樊昌新，曹麗娜.通信原理［M］.北京：國防工業出版社，2008.

［2］馮宇清，李秀亮.基于FPGA的寬頻數字鎖相環設計［J］.艦船電子工程，2012，32（7）：72－75.FENG Yuqing，LI Xiuliang.Design of broadband digital phase－locked loop based on FPGA［J］.Ship Electronic Engineering，2012，32（7）：72－75.

［3］王成，吳瑛，韓廣.基于單頻信號頻率估計的載波頻偏估計算法［J］.信息工程大學學報，2010，11（3）：8－11.WANG Cheng，WU Ying，HAN Guang.Carrier frequency offset estimator based on frequency estimation of single frequency signal［J］.Journal of Information Engineering University，2010，11（3）：8－11.

［4］沈希忠.連續信號頻譜細化算法探討［J］.上海冶金高等專科學校學報，2000（4）：231－235.

［5］丁玉美，高西全.數字信號處理［M］.西安：西安電子科技大學出版社，2005.

［6］海川.高速率遙測信號調制解調技術研究［D］.西安：西安電子科技大學，2008.

［7］遠坂，俊昭.鎖相環（PLL）電路設計與應用［M］.北京：科學出版社，2006