激光散斑照相法測量壓電陶瓷管的電壓響應位移特性

2013-12-01 01:54:22王中平張增明孫臘珍

物理實驗 2013年3期

王中平，張權，朱玲，張增明，孫臘珍

（中國科學技術大學物理學院物理實驗教學中心，安徽合肥230026）

1 引言

壓電陶瓷是微位移驅動、微制動的主要元件，在精密測量和現(xiàn)代科學研究儀器中起著非常重要的作用.壓電陶瓷微驅動器是利用逆壓電效應制作的新型固態(tài)執(zhí)行元件，其具有體積小、驅動電壓低、位移量大、可集成化等特點，在精密光學、微型機械、微電子技術等高新技術領域取得了廣泛地應用，如掃描探針顯微鏡中的掃描器部件與微位移樣品選擇臺.科學家們通過對壓電陶瓷的電壓響應的位移特性進行研究，使得在器件的小型化、微型化以及器件的蠕變性能等方面獲得了很大的改善［1-2］.

研究測量壓電陶瓷電壓響應位移特性的方法有干涉條紋法、光杠桿法等.一般測量壓電陶瓷的壓電與位移關系采用光學相干法，這種方式需要搭建穩(wěn)定的干涉光路，調試操作困難，并且后期數據處理過程相當繁瑣，同時干涉條紋的質量也影響測量的精度［3-6］，對本科生的教學實驗而言實驗難度太大.而單光束激光散斑技術測量位移的光路簡單，成本低，調試操作方便，數據處理方便，本文結合CCD輔助的激光散斑技術可以測定壓電陶瓷管的伸縮量與電壓的關系及其回滯效應，具有直觀、快速、精確的優(yōu)點，適合開展本科生的教學實驗.

2 實驗原理

激光散斑微小位移測量的基本原理見文獻［7］.圖1為實驗原理圖，O1X1軸位于毛玻璃的粗糙表面上，O2X2軸位于觀察平面（CCD探測器表面）上.由激光器出射的光束為高斯光束，實驗中透鏡可以改變光束的發(fā)散角，但根據高斯光束的傳播理論推斷，在近軸區(qū)激光高斯光束經凸透鏡后仍為高斯光束，但束腰位置和尺寸大小會發(fā)生變化［8］.經過凸透鏡的激光光束沿光軸O0O1O2方向入射到毛玻璃的面上，假定其光束束腰位置在O0處，從O0到O1的距離等于P1，從O1到O2的距離為P2.對自相關函數歸一化處理可以求出散斑的平均半徑.而散斑統(tǒng)計平均半徑由理論公式（1）進行計算：

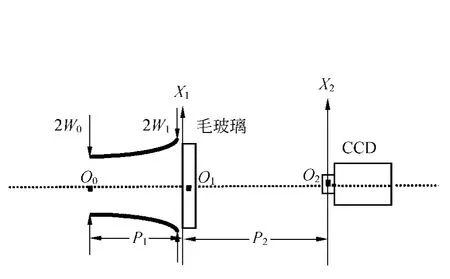
圖1 激光散斑的實驗原理圖

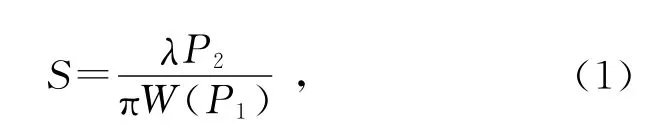
式中W（P1）為照射到毛玻璃的光束的半高半寬，可推斷激光光束的空間分布性質.姚琨等在研究不同光束照明下散斑的規(guī)律時，曾對ρ（P1）和W（P1）對散斑的影響進行了詳細討論［9-15］.可知，當毛玻璃在自身平面內運動時，其散射形成的散斑也會隨之發(fā)生平移，其平移量ΔX與毛玻璃的平移量d0之間的關系為：

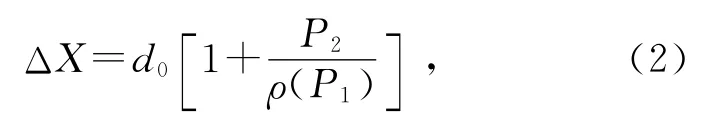
式中ρ（P1）表示照射到毛玻璃表面的高斯光束波陣面的曲率半徑.激光散斑斑圖的平移量ΔX可以運用歸一化的互相關函數關系推導求解，進而得到毛玻璃的面內平移量d0，即壓電陶瓷的電壓驅動伸縮量.

3 實驗裝置和方法

實驗裝置見圖2，凸透鏡L的焦距為50mm.He-Ne激光器出射的激光束經雙偏振器元件對光強進行衰減（以免CCD因曝光量過大而飽和或損傷）后，再經全反射鏡反射至凸透鏡L，經凸透鏡L擴束再照射到疊層型壓電陶瓷頂部的毛玻璃上，這樣在毛玻璃的后面就可以得到客觀散斑場.可通過壓電陶瓷驅動電源（哈爾濱溶智納芯科技有限公司型號：Rhvd1c200v）對壓電陶瓷（型號：PTDC200／5×5／18）施加不同的電壓，驅動壓電陶瓷伸展來移動毛玻璃，使毛玻璃在自身平面內做微小位移.用計算機上的圖像采集程序控制CCD攝像機，對物體發(fā)生位移前后的散斑圖進行采集，CCD像元尺寸為256像元×256像元（CCD像素實際定標校正后1像元＝11.6μm），然后將圖像保存在計算機內，通過編寫程序對散斑圖像進行處理，通過自編寫的線性擬合程序計算散斑在平面內的x和y方向的散斑半徑，再通過計算求出散斑的統(tǒng)計半徑，并計算散斑位移量，即毛玻璃面內位移，也就是壓電陶瓷的電壓驅動位移量的大小.

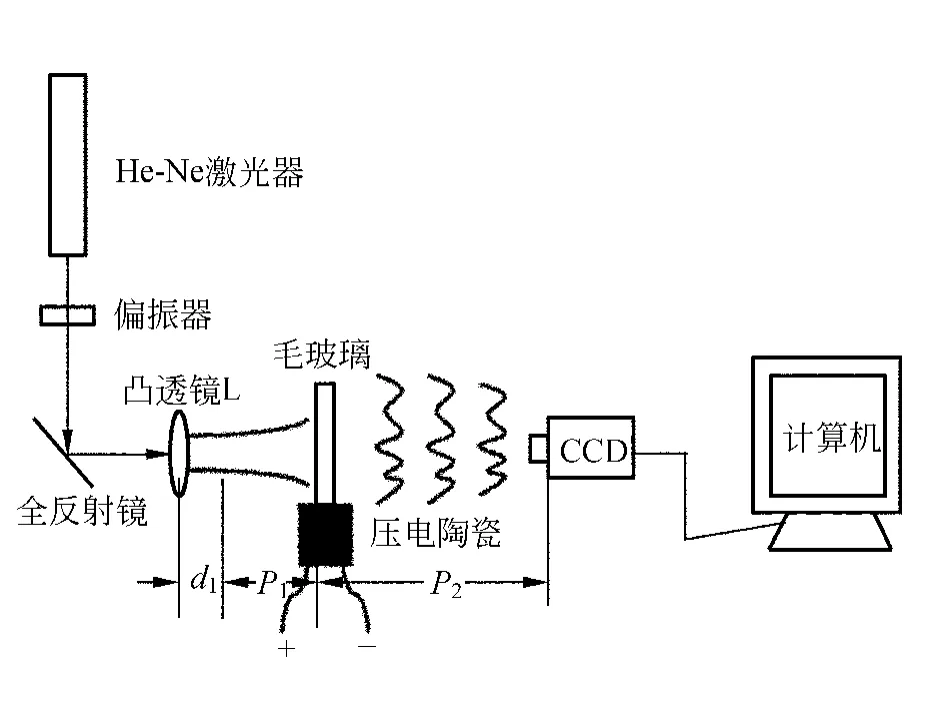
圖2 激光散斑法測量壓電陶瓷位移特性的實驗裝置圖

4 分析討論

實驗采取固定氦氖激光器的激光出射口到凸透鏡的距離（730mm）、凸透鏡到毛玻璃的距離（150mm）以及毛玻璃到CCD接收面的距離（450mm），通過對壓電陶瓷加載不同的電壓改變毛玻璃的微小位移量來研究激光散斑圖像的互相關關系確定微小位移的大小.實驗中選取毛玻璃到CCD接收面的距離450mm為實驗優(yōu)化參量，隨著毛玻璃到CCD接收面的距離逐漸減小，擴束的激光照射到毛玻璃面的擴大，擴束激光的質量為中央清晰明亮，從中心到邊緣光強逐漸衰減，CCD的接收面采集的圖像同樣呈現(xiàn)中央圖像清晰，從中央到邊緣圖像清晰度有所降低，散斑尺寸逐漸變小，清晰度有所降低，但對實驗數據處理結果影響很小，在圖像進行數據處理時，計算機程序自動選擇中央的清晰區(qū)域進行分析計算，所以圖像邊緣效應對測量誤差幾乎沒有影響，可以忽略不計.

通過CCD采集的散斑圖像如圖3所示，可以直觀明晰地分析出散斑半徑的尺寸大小.對壓電陶瓷施加逐漸升高的電壓，待電壓穩(wěn)定后，記錄不同電壓值對應的激光散斑圖像.利用計算機互相關擬合程序，計算每一幅散斑圖與零電壓時散斑圖的互相關關系，可分別得出其散斑圖的像素變化大小.再由式（2）計算出不同電壓值時毛玻璃的面內位移的微小位移量，即壓電陶瓷的電壓響應位移值.圖4給出了壓電陶瓷的不同電壓響應位移曲線與線性擬合曲線.可以看出，實驗的測量結果與生產廠家提供的位移值基本符合.在0～190V的電壓范圍內，壓電陶瓷隨施加電壓的變化基本為線性變化，其位移隨電壓的響應變化率的大小為0.150μm／V（生產廠家的響應變化率的大小為0.148μm／V）.圖5給出了壓電陶瓷隨減載電壓的降低，其位移特性的變化曲線.由于逆電壓效應的存在，電壓位移的響應曲線已經無法滿足線性關系.同時也存在滯后現(xiàn)象，主要是電源內阻過大，壓電陶瓷放電緩慢，雖然在測量回程中盡量延長了放電時間，但電源引起的誤差不可忽略.

圖3 特定P2值下的激光散斑圖像

圖4 加載不同電壓對應的壓電陶瓷的位移響應值與擬合曲線（方塊對應實驗測量值，實心圓對應生產廠家給定值）

本實驗采用光學實驗平臺和磁性表座，利用加載電壓驅動毛玻璃在橫向上發(fā)生微小位移，采取了CCD圖像采集技術和計算機圖像處理技術對單光束激光散斑實驗進行了實驗教學研究.相對于原來的干板成像技術來說，避免了全息干板曝光方法中的諸多不便和繁復，以及再現(xiàn)圖像的精度不夠等缺點，使得實驗操作簡單，現(xiàn)象直觀，易于觀察.但在實驗中需注意驅動電源的電壓穩(wěn)定性對壓電陶瓷造成的影響.同時系統(tǒng)誤差主要來自于激光器的起伏，探測器的噪聲以及光學平臺的穩(wěn)定性能等方面.本實驗同時存在非常大的提升空間，可以鼓勵學生利用顯微激光散斑相關法以及主觀散斑的光路及散斑相關法等不同的研究方法來對壓電陶瓷的電壓響應位移曲線進行實驗研究.

圖5 減載不同電壓對應的壓電陶瓷的位移響應值與擬合曲線（方塊與實線對應實驗測量值，實心圓與虛線對應生產廠家給定值）

5 結束語

采用CCD輔助激光散斑互相關技術方法研究測量壓電陶瓷的壓電位移特性并標定其線性區(qū)間，該方法測量光路簡單，且對系統(tǒng)儀器的裝配誤差要求低，實現(xiàn)了實驗操作的簡單化、實驗現(xiàn)象的直觀化以及現(xiàn)代化新技術在實驗教學中的利用.了解壓電陶瓷的電壓位移響應特性以及逆壓電效應的存在對其影響，讓學生進一步認知在現(xiàn)代科學儀器中具有非常重要應用價值的壓電陶瓷的應用原理與作用機制.現(xiàn)代化的實驗教學方法在優(yōu)化實驗教學模式的同時，也拓展了學生的知識層面，使學生在課堂上所學習的理論和實驗中觀察到的現(xiàn)象有機地結合在一起，激發(fā)了學生對實驗學習的興趣和積極性，為學生發(fā)揮創(chuàng)造性思維提供了基礎.

［1］宋道仁，肖明山.壓電效應及其應用［M］.北京：科學普及出版社，1987.

［2］李龍士.美國開發(fā)壓電陶瓷材料的現(xiàn)狀和動態(tài)［J］.材料導報，1992，（6）：67-69.

［3］劉培森.散斑統(tǒng)計光學基礎［M］.北京：科學出版社，1983：1-50.

［4］丹銻J C.激光斑紋及其有關現(xiàn)象［M］.黃天樂，等譯.北京：科學出版社，1981：1-76.

［5］蔡文貴.CCD技術及應用［M］.北京：電子工業(yè)出版社，1992：1-98.

［6］劉家恕，李強，朱箭.數字圖像處理技術在疊柵條紋測量中的應用［J］.物理實驗，2011，31（2）：40-42.

［7］王中平，張權，朱玲，等.CCD成像輔助激光散斑實驗［J］.物理實驗，2010，30（10）：11-14.

［8］黃水平，郭旭東，張飛雁，等.擬合法測量高斯光束的束腰半徑［J］.物理實驗，2010，30（3）：29-31.

［9］姚焜，侯碧輝，張增明，等.散斑位移法測量高斯光束的空間分布［J］.強激光與粒子束，2000，12（2）：141-144.

［10］高翔，楊白久，何焰藍，等.用激光散斑法測鹽水溶液濃度的改進［J］.物理實驗，2007，27（2）：42-45.

［11］姚焜，陳蝶萍，張權，等.散斑位移量與照明光束特性關系的實驗研究［J］.物理實驗，2003，12（11）：6-9.

［12］軒植華，霍劍青，姚琨，等.大學物理實驗（第三冊）［M］.2版.北京：高等教育出版社，2006：14-22.

［13］李曉英，郎曉萍.激光散斑位移測量方法研究［J］.北京機械工業(yè)學院學報，2008，23（1）：39-42.

［14］邱建軍，張紅艷，駱衛(wèi)華，等.像面散斑平均尺寸對激光散斑成像的影響［J］.光學學報，2009，29（7）：1863-1867.