坡代數上的模糊軟子坡

趙 虎,李生剛,陳桂秀,2

(1.陜西師范大學 數學與信息科學學院,西安 710062;2.青海師范大學 數學系,西寧 810008)

0 引言與預備知識

模糊集、 粗糙集、 Vague集等理論在處理不確定性問題時,都具有參數工具理論不充分的缺陷,為此,Molodtsov[1]提出了基于參數集軟集的概念.目前,軟集[2]已應用于決策分析[2-3]、 模糊軟集[4]、 模糊軟群[5]和模糊軟半群[6]等諸多領域.文獻[7-12]給出了坡代數和軟集合上的結構研究.基于此,本文以模糊軟集為工具,給出了坡代數上模糊軟子坡的概念,并對其性質進行研究.此外,定義了坡代數上模糊軟子坡間的模糊軟同態和模糊軟同構,給出了坡代數上模糊軟子坡的同構像定理和同態逆像定理,證明了坡代數上的模糊軟子坡范疇是坡代數范疇上的拓撲范疇.

定義1[4]X上的一個模糊軟集是一個偶對(f,A)(這里A?E且E是一個非空參數集),且f:A→IX是一個映射,即對于每個e∈A,f(e)=fe:X→I是X上的模糊集合.

定義2[4]設X上的兩個模糊軟集為(f,A)和(g,B),如果(f,A)和(g,B)滿足: 1)A?B;2) ?e∈A,fe≤ge.則稱(f,A)是(g,B)的模糊軟子集,即fe是ge的模糊子集,記為(f,A)?(g,B).

定義3[4]設(f,A)和(g,B)是X上的兩個模糊軟集,如果(f,A)?(g,B)且(g,B)?(f,A),則稱(f,A)和(g,B)是相等的模糊軟集.

定義4[4]設(f,A)和(g,B)是X上的兩個模糊軟集,如果C=A∪B,且

則稱(f,A)和(g,B)的并是一個模糊軟集(h,C).記為(f,A)∪(g,B)=(h,C).

定義5[4]設(f,A)和(g,B)是X上的兩個模糊軟集,如果C=A∩B且he=fe∧ge(?e∈C),則稱(f,A)和(g,B)的交是一個模糊軟集(h,C),記為(f,A)∩(g,B)=(h,C).

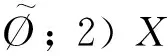
定義7[5]設(f,A)和(g,B)分別是X和Y上的模糊軟集,Ξ是X到Y的函數,Θ是從參數A到參數B的函數,定義(Ξ,Θ)如下：(Ξ,Θ)(f,A)=(Ξ(f),Θ(A)),這里Ξ(f)a滿足：對于?a∈Θ(A)及?y∈Y,

定義(Ξ,Θ)-1(g,B)=(Ξ-1(g),Θ-1(B)),這里Ξ-1(g)e(x)=gΘ(e)(Ξ(x))(?e∈Θ-1(B),?x∈X).此時稱偶對(Ξ,Θ)是從X到Y上的模糊軟函數,并稱(Ξ,Θ)(f,A)是(f,A)在模糊軟函數(Ξ,Θ)下的像,(Ξ,Θ)-1(g,B)是(g,B)在模糊軟函數(Ξ,Θ)下的原像.

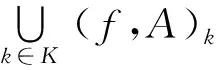
定義9[14]設X是一個集合,若+和·是X上的兩個二元運算且滿足下列條件,則稱(X,+,·)為坡代數:

1)x+y=y+x(?x,y∈X);

2)x+(y+z)=(x+y)+z(?x,y∈X);

3)x·(y·z)=(x·y)·z(?x,y,z∈X);

4)x·(y+z)=(x·y)+(x·z)(?x,y,z∈X);

5) (y+z)·x=(y·x)+(z·x)(?x,y,z∈X);

6)x+x=x(?x∈X);

7)x+(x·y)=x(?x,y∈X);

8)y+(x·y)=y(?x,y∈X).

定義10[14]設(X,+,·)為坡代數,S?X,I?X,F?X.

1) 在X上定義關系≤如下: 對任意的x,y∈X,x≤y當且僅當x+y=y,則≤是X上的一個偏序關系;

2) 若對任意的x,y∈S都有x+y∈S,x·y∈S,則稱S為X的子坡代數;

3) 若I是X的子坡代數并且是一個下集,則稱I為(X,+,·)的理想;

4) 若F是X的子坡代數并且是一個上集,則稱F為(X,+,·)的濾子.

定義11[14]設(X,+,·)和(Y,+,·)為坡代數,f:X→Y為映射.若對任意的x1,x2∈X,有f(x1+x2)=f(x1)+f(x2)和f(x1·x2)=f(x1)·f(x2)成立,則稱f:X→Y為從(X,+,·)到(Y,+,·)的同態.

定義12設(X,+,·)為坡代數,A∈[0,1]X.

1) 如果對任意的x,y∈X,都有A(x+y)∧A(x·y)≥A(x)∧A(y),則稱A為(X,+,·)的模糊子坡代數[14];

2) 如果A既是反序映射又是(X,+,·)的模糊子坡代數,則稱A為(X,+,·)的模糊理想[14];

3) 如果A既是保序映射又是(X,+,·)的模糊子坡代數,則稱A為(X,+,·)的模糊慮子[15].

1 坡代數上的模糊軟子坡

定義13設(X,+,·)是一個坡代數,(f,A)是(X,+,·)上的一個模糊軟集,則(f,A)是(X,+,·)上的一個模糊軟子坡當且僅當對每個e∈A,下式成立：

fe(x+y)∧fe(x·y)≥fe(x)∧fe(y), ?x,y∈X,

即對每個e∈A,fe是文獻[14]意義下的模糊子坡.坡代數(X,+,·)上全體模糊軟子坡記為FSC(X,E).

定義14對(X,+,·)上的模糊軟子坡(f,A),若對每個e∈A,fe都是反序映射(resp.,保序映射),則稱(f,A)是(X,+,·)上的一個模糊軟理想(resp.,模糊軟濾子).坡代數(X,+,·)上全體模糊軟理想(resp.,模糊軟濾子)記為FSI(X,E)(resp.,FSF(X,E)),顯然(FSC(X,E),?),FSI(X,E),?)和(FSF(X,E),?)都是偏序集.

定理1設(X,+,·)為坡代數,則(f,A)是(X,+,·)上的模糊軟子坡(resp.,模糊軟理想,模糊軟濾子),則對任意的α∈[0,1],(f,A)[α]的非空成員是(X,+,·)的子坡代數(resp.,理想,濾子),其中(f,A)[α]={(fe)[α]|e∈A},這里(fe)[α]={x∈X|fe(x)≥α}是模糊集fe的α截集(即(f,A)[α]是經典軟集).

證明: 只證明模糊軟理想的情形.假設存在e∈A,使得(fe)[α]≠?,對任意的x,y∈(fe)[α],由(f,A)是(X,+,·)上的模糊軟濾子知,fe(x)≥α,fe(y)≥α,因此

fe(x+y)≥fe(x+y)∧fe(x·y)≥fe(x)∧fe(y)≥α,

fe(x·y)≥fe(x+y)∧fe(x·y)≥fe(x)∧fe(y)≥α,

于是x+y∈(fe)[α],x·y∈(fe)[α],從而(fe)[α]為(X,+,·)的子坡代數.對任意的x0∈(fe)[α]及任意的x∈X且x0≤x,由(f,A)是(X,+,·)上的模糊軟濾子知fe是保序映射,從而fe(x)≥fe(x0)≥α.于是x∈(fe)[α],表明(fe)[α]是(X,+,·)的上集.

例11) 設X={a,b,c},是所有自然數的集合 ,定義加法與乘法如下:

則可證(X,+,·)為坡代數.定義f:→IX如下：fn:X→I(?n∈),

則偶對(f,)是(X,+,·)上的一個模糊軟集,且可以驗證(f,)是坡代數(X,+,·)上的一個模糊軟理想.

2) (X,+,·)為如1)所示的坡代數,是所有自然數的集合.定義g:→IX如下：gn:X→I(?n∈),

則偶對(g,)是(X,+,·)上的一個模糊軟集,且可以驗證(g,)是坡代數(X,+,·)上的一個模糊軟濾子.

定理2設(f,A)和(g,B)是坡代數(X,+,·)上的兩個模糊軟子坡(resp.,模糊軟理想,模糊軟濾子),則(f,A)∩(g,B)是坡代數(X,+,·)上的模糊軟子坡(resp.,模糊軟理想,模糊軟濾子).

證明: 只證明模糊軟理想的情形.設(f,A)∩(g,B)=(h,C),這里C=A∩B且he=fe∧ge(?e∈C).首先,對任意的x,y∈X,

he(x+y)∧he(x·y)≥he(x)∧he(y).

從而 (f,A)∩(g,B)是坡代數(X,+,·)上的模糊軟子坡.其次,設x,y∈X且x≤y,注意到(f,A)和(g,B)是坡代數(X,+,·)上的兩個模糊軟理想,有he(x)=(fe∧ge)(x)=fe(x)∧ge(x)≥fe(y)∧ge(y)=(fe∧ge)(y)=he(y).因此(f,A)∩(g,B)是坡代數(X,+,·)上的模糊軟理想.

類似定理2的證明,可以證明如下定理成立：

定理4設(f,A)和(g,B)是坡代數(X,+,·)上的模糊軟子坡(resp.,模糊軟理想,模糊軟濾子),則(f,A)∪(g,B)是坡代數(X,+,·)上的模糊軟子坡(resp.,模糊軟理想,模糊軟濾子).

證明: 只證明模糊軟理想的情形.設(f,A)∪(g,B)=(h,C),若e∈A-B,則he=fe;若e∈B-A,則he=ge,根據定義13知結論成立.現設e∈A∩B,首先,由he=fe∨ge(?e∈C),有

因此(f,A)∪(f,B)是坡代數(X,+,·)上的模糊軟子坡.其次,設x,y∈X且x≤y,注意到(f,A)和(g,B)是坡代數(X,+,·)上的兩個模糊軟理想,有

he(x)=(fe∨ge)(x)=fe(x)∨ge(x)≥fe(y)∨ge(y)=(fe∨ge)(y)=he(y).

所以(f,A)∪(g,B)是坡代數(X,+,·)上的模糊軟理想.

類似定理4的證明,可以證明如下定理成立：

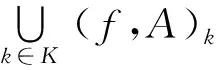
由定理3和定理5,可得:

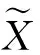
2 坡代數上模糊軟子坡間的同態

定義15設(Ξ,Θ)是從X到Y上的模糊軟函數,若Ξ是從坡代數(X,+,·)到坡代數(Y,+,·)的同態,則稱(Ξ,Θ)是從坡代數X到坡代數Y模糊軟子坡間的同態.若Ξ是從X到Y的同構,且Θ是從A到B的一一映射,則稱(Ξ,Θ)是模糊軟子坡間的同構.

定理7設(g,B)是坡代數Y上的模糊軟子坡(resp.,模糊軟理想,模糊軟濾子),(Ξ,Θ)是從坡代數X到坡代數Y模糊軟子坡間的同態,則(Ξ,Θ)-1(g,B)是坡代數X上的模糊軟子坡(resp.,模糊軟理想,模糊軟濾子).

證明: 只證明模糊軟理想的情形.首先,對于任意的e∈Θ-1(B),

從而(Ξ,Θ)-1(g,B)是坡代數X上的模糊軟子坡.其次,設x,y∈X且x≤y,則x+y=y,此時由(Ξ,Θ)是從坡代數X到坡代數Y的模糊軟子坡間的同態知Ξ(x)+Ξ(y)=Ξ(x+y)=Ξ(y),即Ξ(x)≤Ξ(y),再由(g,B)是坡代數Y上的模糊軟子坡知,對于任意的e∈Θ-1(B),

Ξ-1(g)e(x)=gΘ(e)(Ξ(x))≥gΘ(e)(Ξ(y))=Ξ-1(g)e(y),

因此,(Ξ,Θ)-1(g,B)是坡代數X上的模糊軟理想.

定理8設(f,A)是坡代數X上的模糊軟子坡(resp.,模糊軟理想,模糊軟濾子),(Ξ,Θ)是從坡代數X到坡代數Y模糊軟子坡間的同構,則(Ξ,Θ)(f,A)是坡代數Y上的模糊軟子坡(resp.,模糊軟理想,模糊軟濾子).

證明: 只證明模糊軟理想的情形.首先,由(Ξ,Θ)是從坡代數X到坡代數Y模糊軟子坡間的同構知,若y1,y2∈Y,則存在唯一的x1,x2∈X和唯一的e∈A,使得Ξ(x1)=y1Ξ(x2)=y2,Ξ(e)=a,此時

因此(Ξ,Θ)(f,A)是坡代數Y上的模糊軟子坡.其次,設y1,y2∈Y且y1≤y2,則存在唯一的x1,x2∈X,使得Ξ(x1)=y1Ξ(x2)=y2,必有x1=Ξ-1(Ξ(x1))≤Xi-1(Ξ(x2))=x2,由于(f,A)是坡代數X上的模糊軟理想,所以

因此(Ξ,Θ)(f,A)是坡代數Y上的模糊軟理想.

3 坡代數上模糊軟子坡的范疇性質

用FSINC表示所有模糊軟子坡的范疇,規定其態射如下：對任意的FSINC-對象f∈FSC(X1,E1)和g∈FSC(X2,E2),ΞΘ∈hom(f,g)當且僅當ΞΘ是從坡代數X到坡代數Y模糊軟子坡間的同態,且對于任意的x∈X1和e1∈E1,有fe1(x)≤gΘ(e1)(Ξ(x)).

證明: ?x,y∈X及?e∈E,由{Ξj|X→Xj}j∈J是一族坡代數間的同態,有

所以f是坡代數X上的模糊軟子坡,且易證ΞjΘj∈hom(f,fj).

定理10設FSINC對象g∈FSC(Y,F),ΦΨ∈hom(g,f) ?ΞjΘj°ΦΨ∈hom(g,fj)(?i∈J),這里Φ:Y→X,Ψ:F→E是映射.

證明: 一方面,若ΦΨ∈hom(g,f),則ΦΨ是從坡代數Y到坡代數X模糊軟子坡間的同態,且對于任意的y∈Y和e1∈F,有ge1(y)≤fΨ(e1)(Φ(y)).由定理9知,ΞjΘj∈hom(f,fj),即ΞjΘj是從坡代數X到坡代數Xj模糊軟子坡間的同態,因此ΞjΘj°ΦΨ是從坡代數Y到Xj模糊軟子坡間的同態,且

ge1(y)≤fΨ(e1)(Φ(y))≤(fj)Θj(Ψ(e1))(Ξj(Φ(y))).

即ΞjΘj°ΦΨ∈hom(g,fj)(?i∈J).

另一方面,若ΞjΘj°ΦΨ∈hom(g,fj)(?i∈J),對于任意的y∈Y和e1∈F,有ge1(y)≤(fj)Θj(Ψ(e1))(Ξj(Φ(y))),且ΞjΘj°ΦΨ從坡代數Y到坡代數Xj模糊軟子坡間的同態.由f的定義知,

利用反證法易證ΦΨ是從坡代數Y到坡代數X模糊軟子坡間的同態,因此ΦΨ∈hom(g,f).

定理11若f′也是坡代數X上的模糊軟子坡,使得ΞjΘj∈hom(f′,fj)(?j∈J),則f=f′.

由定理9～定理11可得：

定理12范疇FSINC是INC(即坡代數及坡代數同態的范疇)上的拓撲范疇.

[1] Molodtsov D.Soft Set Theory: First Results [J].Computers and Mathematics with Applications,1999,37(4/5): 19-31.

[2] Maji P K,Biswas R,Roy A R.Soft Set Theory [J].Computers and Mathematics with Applications,2003,45(4/5): 555-562.

[3] KONG Zhi,GAO Li-qun,WANG Li-fu.Comment on “A Fuzzy Soft Set Theoretic Approach to Decision Making Problems” [J].Journal of Computational and Applied Mathematics,2009,223(2): 540-542.

[4] Maji P K,Biswas R,Roy A R.Fuzzy Soft Sets [J].Journal of Fuzzy Mathematics,2001,9(3): 589-602.

[5] Aygünoglu A,Aygün H.Introduction to Fuzzy Soft Groups [J].Computers and Mathematics with Applications,2009,58(6): 1279-1286.

[6] YANG Cheng-fu.Fuzzy Soft Semigroups and Fuzzy Soft Ideals [J].Computers and Mathematics with Applications,2011,61(2): 255-261.

[7] MA Xue-ling,ZHAN Jian-ming.Intuitionistic Fuzzy Ideals of Incline Algebras [J].Sci Math Jpn,2005,62(1): 85-90.

[8] ZHAN Jian-ming,MA Xue-ling.Doubt Fuzzy Subinclines (Ideals) of Incline Algebras [J].Sci Math Jpn,2005,61(2): 313-318.

[9] ZHAN Jian-ming,LONG Ming.T-Fuzzy Ideals of Incline Algebras [J].Sci Math Jpn,2005,62(1): 135-141.

[10] YIN Yun-qiang,ZHAN Jian-ming.Fuzzy Soft Polygroups [J].Acta Math Sinica: Chin Ser,2012,55(1): 117-130.(殷允強,詹建明.模糊軟P-超群 [J].數學學報: 中文版,2012,55(1): 117-130.)

[11] ZHAN Jian-ming,Dudek W A.Soft MTL-Algebras Based on Fuzzy Sets [J].Politehn Univ Bucharest Sci Bull Ser A: Appl Math Phys,2012,74(2): 41-56.

[12] ZHAN Jian-ming,XU Yang.Soft Lattice Implication Algebras Based on Fuzzy Sets [J].Hacet J Math Stat,2011,40(4): 483-492.

[13] Tanay B,Kandemir M B.Topological Structure of Fuzzy Soft Sets [J].Computers and Mathematics with Applications,2011,61(10): 2952-2957.

[14] Jun Y B,Ahn S S,Kim H S.Fuzzy Subinclines (Ideals) of Incline Algebras [J].Fuzzy Sets and Systems,2001,123(5): 217-225.

[15] LIU Lu-lu,FU Wen-qing,LI Sheng-gang.The Order Aspects of Fuzzy Subinclines,Fuzzy Equivalence Relations,and Fuzzy Congruence Relations [J].Fuzzy Systems and Mathematics,2011,25(5): 43-49.(劉璐璐,伏文清,李生剛.模糊子坡代數、 模糊等價關系及模糊同余關系的序方面 [J].模糊系統與數學,2011,25(5): 43-49.)