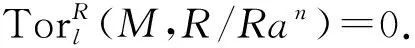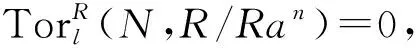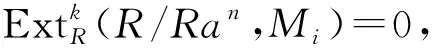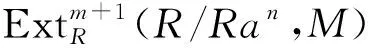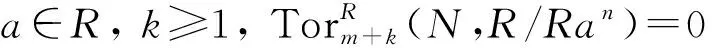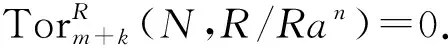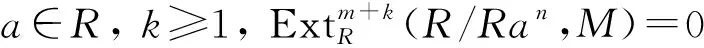廣義P-平坦性和廣義P-內(nèi)射性的一些刻畫

王修建,杜先能

(1.皖西學(xué)院 應(yīng)用數(shù)學(xué)學(xué)院,安徽 六安 237012;2.安徽大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,合肥 230600)

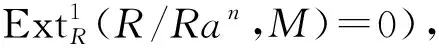
1 GP-內(nèi)射環(huán)、 GPP-環(huán)和GPF-環(huán)

定義1[1]如果R作為左R-模是GP-內(nèi)射的,則稱環(huán)R為左GP-內(nèi)射環(huán).

定理1對(duì)于環(huán)R,下述結(jié)論等價(jià)：1)R是左GP-內(nèi)射環(huán);2) 對(duì)任意的a∈R,存在正整數(shù)n,使得anR=rRlR(an);3) 對(duì)任意的a,b∈R,如果lR(an)?lR(bn),則bnR?anR;4) 對(duì)任意的a,b∈R,存在一正整數(shù)n,使得rR(Rbn∩lR(an))=rR(bn)+anR.

證明: 1)?2)顯然.

2)?3).如果lR(an)?lR(bn),則bn?rRlR(an),故由2)知bn∈anR,因此bnR?anR.

3)?4).對(duì)于任意的a,b∈R,rR(Rbn∩lR(an))?rR(bn)+anR顯然.反之,如果x∈rR(Rbn∩lR(an)),則Rbn∩lR(an)?lR(x);如果y∈lR(bnan),則ybnan=0,因此ybn∈lR(an),即ybn∈Rbn∩lR(an)?lR(x),從而y∈lR(bnx)(即證lR(bnan)?lR(bnx)).由3)知存在r∈R,使得bnx=bnanr,因此x-anr∈rR(bn),即證x∈rR(bn)+anR.又由x的任意性知,rR(Rbn∩lR(an))?rR(bn)+anR.

4)?2).令b=1即可證結(jié)論.

定義2[1]如果對(duì)于任意的a∈R,存在一個(gè)正整數(shù)n(依賴于a),使得Ran是投射的,則稱環(huán)R為左GPP-環(huán);如果對(duì)于任意的a∈R,存在一個(gè)正整數(shù)n(依賴于a),使得Ran是平坦的,則稱環(huán)R為左GPF-環(huán).顯然,左GPF環(huán)是左GPP-環(huán)和左PF-環(huán)的推廣.

定理2對(duì)于環(huán)R,下述結(jié)論等價(jià)：1)R為左GPP環(huán)； 2) 任意GP-內(nèi)射左R-模的商模是GP-內(nèi)射的； 3) 任意P-內(nèi)射左R-模的商模是GP-內(nèi)射的； 4) 任意內(nèi)射左R-模的商模是GP-內(nèi)射的； 5) 對(duì)于任意的左R-模M,都有E(M)/M是GP-內(nèi)射的,其中E(M)為M的內(nèi)射包.

證明: 1)?2).設(shè)M是任意GP-內(nèi)射左R-模且N為M的一個(gè)子模,下證M/N是GP-內(nèi)射的.事實(shí)上,設(shè)a∈R,則由1)知存在正整數(shù)n,使得Ran是投射的.令i:Ran→R是嵌入映射,π:M→M/N是典范映射,則對(duì)任意映射f:Ran→M/N,都有映射g:Ran→M,使得πg(shù)=f.既然M是GP-內(nèi)射的,因此存在h:R→M,使得hi=g,所以(πh)i=f,即M/N是GP-內(nèi)射的.

2)?3),3)?4)和4)?5)顯然.4)?1)參見文獻(xiàn)[1]中定理3.2.

5)?4).對(duì)任意的左R-模M,設(shè)L→M→0是正合列,其中L是內(nèi)射的,則存在一個(gè)正合列0→M′→L→M→0,因?yàn)長是內(nèi)射左R-模,所以0→E(M′)→L是正合的,從而可得L=E(M′)⊕L′,其中L′是內(nèi)射左R-模.于是可得

M?L/M′?(E(M′)⊕L′)/M′?E(M′)/M′⊕L′.

由5)知E(M′)/M′是GP-內(nèi)射的,而L′是內(nèi)射的,從而為P-內(nèi)射的,故由文獻(xiàn)[1]中命題2.3知M是GP-內(nèi)射的,即任意內(nèi)射左R-模的商模都是GP-內(nèi)射的.

定理3設(shè)R是環(huán),下述結(jié)論等價(jià)：1)R是左GPF-環(huán)； 2) P-平坦右R-模的任一子模都是GP-平坦的； 3) 投射右R-模的任一子模都是GP-平坦的.

證明：1)?2)由文獻(xiàn)[1]中定理3.1即得.2)?3)顯然.

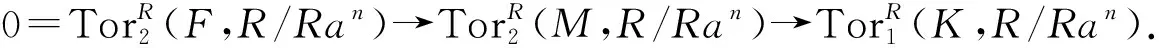
下面記GPI表示所有GP-內(nèi)射左R-模組成的類.

定義3設(shè)K為GP-內(nèi)射左R-模,若對(duì)任意GP-內(nèi)射左R-模K′和任意同態(tài)ψ:K′→M,總存在同態(tài)f:K′→K,使得φf=ψ,則稱同態(tài)φ:K→M為M的GPI-預(yù)覆蓋.如果K的滿足φf=φ的自同態(tài)f是同構(gòu),則稱φ:K→M為M的GPI-覆蓋.

定理4設(shè)R為環(huán),且滿足GP-內(nèi)射模的直和仍為GP-內(nèi)射模,則下述結(jié)論等價(jià)：1)R為左GPP環(huán)； 2) 任一左R-模M有一個(gè)單的GPI-覆蓋φ:K→M； 3) 任一GP-內(nèi)射左R-模M的商模有一個(gè)單的GPI-覆蓋.

證明：1)?2).假設(shè)M是任意的左R-模,記

K=∑{N≤M|N∈GPI},L= ⊕{N≤M|N∈GPI},

則存在0→H→L→K→0是正合的,因?yàn)長仍為GP-內(nèi)射的,因此由定理2知K也為GP-內(nèi)射的,下證嵌入映射l:K→M是M的一個(gè)GPI-覆蓋.設(shè)K′是GP-內(nèi)射左R-模,ψ:K′→M是任意的左R-模同態(tài),則易知ψ(K′)≤K.定義φ:K′→K,φ(x)=ψ(x),x∈K′,則有l(wèi)φ=ψ,因而l:K→M是M的一個(gè)GPI-預(yù)覆蓋.進(jìn)一步,易證使得l=fl成立的同態(tài)f:K→K是K的恒等映射IK且是唯一的,因此2)成立.

2)?3)顯然.

3)?1).設(shè)M是任意的GP-內(nèi)射左R-模且N是M的一個(gè)子模,下證M/N是GP-內(nèi)射的.事實(shí)上,存在內(nèi)射模E,使得0→N→E→L→0是正合的,且記E→L的同態(tài)映射為g.由3)知L有一個(gè)單的GPI-覆蓋φ:F→L,則有同態(tài)h:E→F,使得g=φh,因此φ是滿的,從而φ是同構(gòu)的,進(jìn)而L是GP-內(nèi)射的.對(duì)任意的a∈R,有

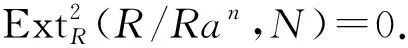
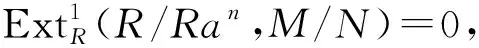
2 GP-內(nèi)射維數(shù)和GP-平坦維數(shù)

定義4設(shè)R為環(huán),左R-模M的GP-內(nèi)射維數(shù)記為GP-id(M),定義為

?a∈R},

其中m為非負(fù)整數(shù).若m不存在,則記為GP-id(M)=∞.環(huán)R的左GP-內(nèi)射整體維數(shù)記為l.GP-iD(R)=sup{GP-id(M)|M為任意左R-模}.

注11) 任給左R-模M是GP-內(nèi)射的當(dāng)且僅當(dāng)GP-id(M)=0;2) 環(huán)R為π-正則環(huán)當(dāng)且僅當(dāng)l.GP-iD(R)=0.

定義5設(shè)R為環(huán),右R-模M的GP-平坦維數(shù)記為GP-fd(M),定義為

?a∈R},

其中m為非負(fù)整數(shù).若m不存在,則記為GP-fd(M)=∞.環(huán)R的右GP-弱維數(shù)記為r.GP-fD(R)=sup{GP-fd(M)|M為任意右R-模}.

注21) 任給右R-模M是GP-平坦的當(dāng)且僅當(dāng)GP-fd(M)=0;2) 環(huán)R為π-正則環(huán)當(dāng)且僅當(dāng)r.GP-fD(R)=0;3) 一般地,r.GP-fD(R)≤l.GP-iD(R).事實(shí)上,假設(shè)l.GP-iD(R)=m<∞,設(shè)M∈Mod-R,則對(duì)任意的a∈R,存在一正整數(shù)k≤m,使得

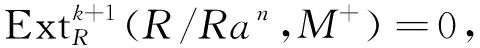
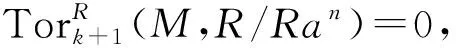
定義6左R-模M的一個(gè)GP-內(nèi)射分解為如下形式的正合列: 0→M→M0→M1→…,其中Mi均為GP-內(nèi)射左R-模.

類似可定義右R-模M的一個(gè)GP-平坦分解.

定理5設(shè)R是環(huán),M為一右R-模,則GP-fd(M)=GP-id(M+).

定理6設(shè)R是左P-凝聚環(huán),M為一左R-模,則GP-id(M)=GP-fd(M+).

假設(shè)GP-fd(M+)=m<∞,則對(duì)任意的a∈R,存在n∈+,使得

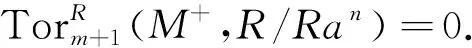
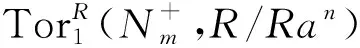
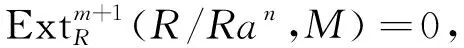
定理7設(shè)R是左P-凝聚環(huán),則r.GP-fD(R)=l.GP-iD(R).

證明：先設(shè)r.GP-fD(R)=m≤∞,則對(duì)任意的左R-模M,由定理6知GP-id(M)=GP-fd(M+)≤m,因此l.GP-iD(R)≤r.GP-fD(R).反之,設(shè)l.GP-iD(R)=n≤∞,則對(duì)任意的右R-模N,由定理5知GP-fd(N)=GP-id(N+)≤n,因此r.GP-fD(R)≤l.GP-iD(R).

定理8設(shè)0→L→M→N→0是右R-模短正合列,則下述結(jié)論成立:

1) 如果r.GP-fd(M)

2) 如果r.GP-fd(M)>r.GP-fd(N),則r.GP-fd(L)=r.GP-fd(M).

證明：對(duì)于任意的a∈R,由長正合列引理得

對(duì)于左R-模的GP-內(nèi)射維數(shù)可得類似結(jié)論.

定理9設(shè)0→L→M→N→0是左R-模短正合列,則下述結(jié)論成立:

1) 如果l.GP-id(M)

2) 如果l.GP-id(M)>l.GP-id(N),則l.GP-id(L)=l.GP-id(M).

定理10對(duì)于任意的左R-模M及a∈R,l.GP-id(M)≤m當(dāng)且僅當(dāng)存在M的一個(gè)GP-內(nèi)射分解0→M→M0→M1→…→Mm→0.

證明：對(duì)于任意的左R-模M及a∈R,設(shè)l.GP-id(M)≤m.取M的一個(gè)GP-內(nèi)射分解:

記該分解的第m-1個(gè)上合沖為Lm-1=Imfm-1,考慮短正合列0→Imfi→Mi→Imfi+1→0,對(duì)于任意的a∈R,則序列

0→M→M0→M1→…→Mm-1→Lm→0.

類似于定理10可證:

定理11對(duì)于任意的右R-模N及a∈R,r.GP-fd(N)≤m當(dāng)且僅當(dāng)存在N的一個(gè)GP-平坦分解0→Nm→…→N1→N0→N→0.

證明：1)?2).由r.GP-fd(N)≤m可知,N有一個(gè)GP-平坦分解:

0→Nm→…→N1→N0→N→0.

3)?1).設(shè)…→Nm→…→N1→N0→N→0是N的一個(gè)GP-平坦分解,令Km-1是它的第m-1個(gè)合沖,則0→Km-1→Nm-1→…→N1→N0→N→0正合,由3)知Km-1也是GP-平坦模,所以r.GP-fd(N)≤m.

對(duì)于GP-內(nèi)射維數(shù),有類似結(jié)論.

推論3設(shè)R是環(huán),下述結(jié)論等價(jià)：1) 每個(gè)GP-平坦右R-模是平坦的； 2) 對(duì)任意的右R-模M,GP-fd(M)=fd(M).

證明：1)?2).設(shè)M是任意的右R-模,由每個(gè)平坦模右R-模都是GP-平坦模易知GP-fd(M)≤fd(M),下證fd(M)≤GP-fd(M).當(dāng)GP-fd(M)=∞時(shí),該不等式顯然成立.現(xiàn)設(shè)GP-fd(M)=m,則由定理11知M有一個(gè)長度為m的GP-平坦分解,由于每個(gè)GP-平坦右R-模都是平坦的,故fd(M)≤n=GP-fd(M),因此GP-fd(M)=fd(M).

2)?1)顯然.

推論4設(shè)R是環(huán)且每個(gè)GP-平坦右R-模是平坦模,則r.wd(R)=r.GP-fd(R),其中r.wd(R)表示環(huán)R的右弱維數(shù).

[1] MAO Li-xin.Generalized P-Flatness and P-Injectivity of Modules [J].Hacettepe J of Mathematics and Statistics,2011,40(1): 27-40.

[2] CHEN Jian-long,DING Nan-qing.On Regularity of Rings [J].Algebra Colloquium,2001,8(3): 267-274.

[3] ZHU Hai-yan,DING Nan-qing.Generalized Morphic Rings and Their Applications [J].Comm in Algebra,2007,35: 2820-2837.

[4] GENG Yu-xian.The P-Cotorsion Dimensions of Modules and Rings [J].Acta Math Scientica,2010,30B(4): 1029-1043.

[5] CHEN Jian-long,DING Nan-qing.Onn-Coherent Rings [J].Comm in Algebra,1996,24(10): 3211-3216.

[6] MAO Li-xin.Onn-P-Injective Modules [J].College Math,2004,20(1): 49-53.

[7] MAO Li-xin,DING Nan-qing.On Divisible and Torsionfree Modules [J].Comm Algebra,2008,36(2): 708-731.

[8] ZHANG Xiao-xiang,CHEN Jian-long,ZHANG Juan.On (m,n)-Injective Modules and (m,n)-Coherent Rings [J].Algebra Colloq,2005,12(1): 149-160.

[9] ZHANG Ju-le,WU Jun.Generalizations of Principal Injectivity [J].Algebra Colloq,1999(6): 277-282.

[10] XIANG Yue-ming.Generalized Injectivity of Rings and Modules and Its Applications [D].Changsha: Hunan Normal University,2010.(向躍明.環(huán)模的廣義內(nèi)射性及其應(yīng)用 [D].長沙：湖南師范大學(xué),2010.)