廣義Ⅰ型一致不變凸條件下的極大極小分式規(guī)劃的二階對偶

焦合華,劉三陽

(1.西安電子科技大學 理學院,西安 710071； 2.長江師范學院 數(shù)學與計算機學院,重慶 408100)

0 引 言

函數(shù)的凸性在數(shù)學規(guī)劃如最優(yōu)性和對偶性等方面具有重要作用,目前的研究都致力于弱化凸性條件以擴大其應用范圍,并取得了豐富成果[1-13].而極大極小分式規(guī)劃是數(shù)學規(guī)劃的一種重要類型,在投資組合選擇、 多目標規(guī)劃、 工程設計等領(lǐng)域應用廣泛.文獻[2-4]研究了如下極大極小分式規(guī)劃(P)的最優(yōu)性和對偶性:

其中:S={x∈X:g(x)≤0}為(P)的可行集;X?n開;Y?l緊.設f,h:X×Y→和g:X→m關(guān)于x的一、 二階偏導數(shù)均連續(xù),并且對?(x,y)∈S×Y,f(x,y)≥0,h(x,y)>0.Mangasarian[5]在一類非線性規(guī)劃中建立了二階對偶模型,并得到了一些對偶結(jié)果;Bector等[6]在一類廣義不變凸條件下建立了極大極小規(guī)劃的二階對偶定理;Liu[7]利用二階廣義B-不變凸推廣了文獻[6]的相應結(jié)果;Mishra等[8]利用廣義Ⅰ型函數(shù)建立了不可微極大極小規(guī)劃的二階對偶定理;Husain等[9]在一類廣義凸條件下,分別證明了不可微極大極小規(guī)劃的Mangasarian型和Mond-Weir型二階對偶定理;Husain等[10]和Sharma等[11]分別在兩種不同廣義凸條件下建立了極大極小分式規(guī)劃問題(P)的二階對偶定理.Ahmad等[12]在二階(F,α,ρ,d)-Ⅰ型條件下,證明了一類不可微極大極小規(guī)劃的二階Wolfe型和Mond-Weir型對偶定理;Jayswal等[13]在(F,α,ρ,θ)-d-Ⅴ一致不變凸條件下,得到了一類非光滑多目標規(guī)劃問題的幾個最優(yōu)性充分條件和Mond-Weir型對偶定理.

基于上述結(jié)果,本文利用二階(F,α,ρ,d)-Ⅰ型函數(shù)和(F,α,ρ,θ)-d-Ⅴ一致不變凸函數(shù),提出二階廣義(F,α,ρ,θ)-d-Ⅴ-Ⅰ型一致不變凸的概念,建立了極大極小分式規(guī)劃問題(P)的一個二階對偶模型,并在此二階廣義Ⅰ型一致不變凸條件下,討論了其弱對偶、 強對偶和嚴格逆對偶定理.

1 預備知識

令M={1,2,…,m},對?x∈S,規(guī)定：

K(x)={(s,t,u)∈

u=(y1,y2,…,ys),yi∈Y(x),i=1,2,…,s}.

定義1[12]稱函數(shù)F:X×X×n→關(guān)于第三變量是次線性的,如果對?滿足:

設α=(α0,α1): (X×X)→+{0},ρ=(ρ0,ρ1)∈×,b0,b1:X×X→+,φ0,φ1:→,d:→(滿足d(0)=0),θ:X×X→+(滿足?并設φ,ω:X→在處都是二階可微的,“”表示關(guān)于x的梯度向量.

利用文獻[12]中二階(F,α,ρ,d)-Ⅰ型函數(shù)和文獻[13]中(F,α,ρ,θ)-d-Ⅴ一致不變凸函數(shù),引入如下定義.

定義2若對?x∈S,p∈n,存在d,θ,bt,φt,αt,ρt(t=0,1)和函數(shù)F,使得

2 對偶性

下面建立極大極小分式規(guī)劃(P)的二階對偶模型(D),并在二階廣義(F,α,ρ,θ)-d-Ⅴ-Ⅰ型一致不變凸條件下證明其弱對偶、 強對偶和嚴格逆對偶定理.

定理2(弱對偶) 設x和(z,μ,λ,s,t,u,p)分別為規(guī)劃(P)和對偶(D)的可行解,并且:

2)φ0(a)≥0?a≥0,a≥0?φ1(a)≥0,b0(x,z)>0,b1(x,z)≥0;

3)α0(x,z)=α1(x,z),ρ0≥-ρ1.

證明：因為a≥0?φ1(a)≥0,b1(x,z)≥0,所以由式(6)可得

再由條件1)的第二部分,可得

利用式(4)和F的次線性,可得

考慮條件3),可得

再根據(jù)條件1)的第一部分,又可得

由b0(x,z)>0,φ0(a)≥0?a≥0和式(5),可得

故存在某個i0,使得

ti0(f(x,yi0)-λh(x,yi0))≥0,

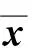
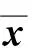
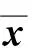
再由條件2)中第二部分可得

利用式(4)和函數(shù)F的次線性可知

根據(jù)條件4),有

再由條件2)中第一部分可得

因此存在i0,使得

[1] JIAO He-hua,LIU San-yang.Nondifferentiable Multiobjective Programming Problem under GeneralizeddⅠ-Ⅴ-Type-Ⅰ Univexity [J].Journal of Jilin University: Science Edition,2012,50(3): 391-396.(焦合華,劉三陽.廣義dI-Ⅴ-Ⅰ型一致不變凸條件下的不可微多目標規(guī)劃問題 [J].吉林大學學報: 理學版,2012,50(3)：391-396.)

[2] Chandra S,Kumar V.Duality in Fractional Minimax Programming [J].J Aust Math Soc: Ser A,1995,58: 376-386.

[3] Liu J C,Wu C S.On Minimax Fractional Optimality Conditions with (F,ρ)-Convexity [J].J Math Anal Appl,1998,219(1): 36-51.

[4] YANG Xin-ming,HOU Shui-hung.On Minimax Fractional Optimality and Duality with Generalized Convexity [J].J Glob Optim,2005,31(2): 235-252.

[5] Mangasarian O L.Second and Higher Order Duality in Nonlinear Programming [J].J Math Anal Appl,1975,51(3): 607-620.

[6] Bector C R,Chandra S,Husain I.Second Order Duality for a Minimax Programming Problem [J].Opsearch,1991,28: 249-263.

[7] Liu J C.Second Order Duality for Minimax Programming [J].Util Math,1999,56: 53-63.

[8] Mishra S K,Rueda N G.Second-Order Duality for Nondifferentiable Minimax Programming Involving Generalized Type Ⅰ Functions [J].J Optim Theory Appl,2006,130(3): 477-486.

[9] Husain Z,Jayswal A,Ahmad I.Second Order Duality for Nondifferentiable Minimax Programming Problems with Generalized Convexity [J].J Glob Optim,2009,44: 593-608.

[10] Husain Z,Ahmad I,Sharma S.Second Order Duality for Minimax Fractional Programming [J].Optim Lett,2009,3(2): 277-286.

[11] Sharma S,Gulati T R.Second Order Duality in Minimax Fractional Programming with Generalized Univexity [J].J Glob Optim,2012,52(1): 161-169.

[12] Ahmad I,Husain Z,Sharma S.Second-Order Duality in Nondifferentiable Minimax Programming Involving Type-Ⅰ Functions [J].J Comput Appl Math,2008,215: 91-102.

[13] Jayswal A,Ahmadb I,Al-Homidanb S.Sufficiency and Duality for Nonsmooth Multiobjective Programming Problems Involving Generalized (F,α,ρ,θ)-d-Ⅴ Univex Functions [J].Math Comput Model,2011,53(1/2): 81-90.