多參數二階脈沖時滯系統極值解的存在性

趙 昕,王淑玲,白 杰

(1.吉林農業大學 信息技術學院,長春 130118;2.東北師范大學人文學院,長春 130117)

脈沖時滯微分方程理論已成為微分方程理論的重要組成部分[1].具有脈沖效應的泛函微分方程邊界問題解的存在性研究目前已受到人們廣泛關注,并得到了許多有意義的結果[2-9].多參數泛函系統的研究對生物種群的研究具有重要意義,對于參數化邊界值問題解的存在性研究近年已取得一些進展[10-17].但關于帶參數二階脈沖時滯微分方程邊值問題的研究目前報道較少.本文考慮如下邊界值問題(BVP):

(1)

其中:f∈C(J××D×n,);gi∈C(×,);D=L1([-τ,0],×n,);0≤t1≤t2≤…≤tm≤T;J0=[-τ,T];ΔΔk=1,2,…,m;常數τ>0.

定義1如果(α0,γ0)滿足下列條件,則(α0,γ0)稱為問題(1)的上解:

定義2如果(β0,ζ0)滿足下列條件,則(β0,ζ0)稱為問題(1)的下解:

令J-=J{t1,t2,…,tm},PC(J0,)={u:J0;當t≠tk時u(t)連續,存在,且(J,)={u:J;當t≠tk時u′(t)連續,u′(存在,且k=1,2,…,m}.顯然E={u∈PC′(J,)}為Banach空間,其范數為‖u‖PC′=max{‖u(t)‖PC,‖u′(t)‖PC′},其中‖u(t)‖PC=max{|u(t)|:t∈J0},‖u′(t)‖PC=max{|u′(t)|:t∈J}.

先考慮線性邊值問題(BVP):

(2)

仿照文獻[12,14]主要結果的證明， 可得下列3個引理.

引理1u∈E∩C2(J-,)是方程(2)的解,當且僅當u∈PC(J,)滿足脈沖積分方程

則方程(2)有唯一解u∈E.

定義J0=(t0,t1],J1=(t1,t2],…,Jm=(tm,tm+1],a=max{tk-tk+1,k=0,1,…,m},t0=0,tm+1=T.

引理3假設p∈E∩C2(J-,)滿足:

(4)

假設條件:

(H1) (α0,γ0),(β0,γ1)是方程(1)的上下解,且(α0,γ0)≤(β0,γ1);

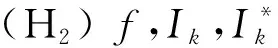
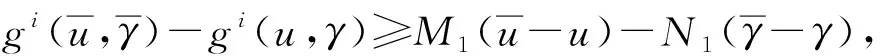
其中α0≤v(tk)≤u(tk)≤β(tk),k=1,2,…,m;

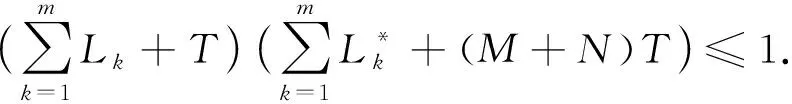
定理1假設條件(H1)～(H6)成立,且

(5)

則在[α0,β0]×[γ0,ζ0]上必存在單調序列{(αn(t),γn)}和{(βn(t),ζn)}?(E∩C2(J-,))×n,并分別收斂于邊值問題(1)的極值解.

證明: 對于任意的(η,γ)∈[α0,β0]×[γ0,ζ0],考慮如下線性邊值問題:

(6)

其中σ(t)=f(t,η(t),ηt,γ)+Mη(t)+Nηt.

由引理2可知,線性邊值問題(6)有唯一解(u,μ)∈E×n.定義算子A,使得A(η,γ)=(u,μ).易證: 1) (α0,γ0)≤A(α0,γ0),(β0,ζ0)≥A(β0,ζ0);2)A在[α0,β0]×[γ0,ζ0]是增算子.

為證明1),設A(α0,γ0)=(α1,a),A(β0,ζ0)=(β1,b).先證明(α0,γ0)≤(α1,a).

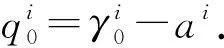
又由引理3可知,p0(t)≤0,t∈J0,i.e.,α(t)≤α1(t).再根據式(6),得

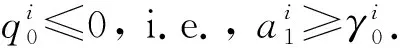
由引理3可知,p1(t)≤0,t∈J0,i.e.,u1(t)≤u2(t).再根據式(6)和假設條件(H4),有

令(αn,γn)=A(αn-1,γn-1),(βn,ζn)=A(βn-1,ζn-1),n=1,2,…,可構造序列{(αn(t),γn)}和{(βn(t),ζn)},使得

顯然,(αi,γi),(βi,ζi)(i=1,2,…)滿足:

根據引理3,有p(t)≤0,i.e.,αn+1(t)≤u(t),?t∈J.由條件(H4)可知

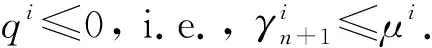
同理可以證明u(t)≤βn+1(t)(t∈J),μ≤ζn+1(t∈J).從而(αn+1,γn+1)≤(u,μ)≤(βn+1,ζn+1),所以(α*,γ*)≤(u,μ)≤(β*,ζ*).證畢.

注1實際上,同理也可以證明下列線性邊值問題極值解的存在性:

(7)

其中:fi∈C(J××D×n,);gi∈C(×,);D=L1([-τ,0],×n,);0≤t1≤t2≤…≤tm≤T;J0=[-τ,T];ΔΔk=1,2,…,m;τ>0;cj(j=1,2,…,n1)為常數.

[1] Lakshmikantham V,Bainov D,Simeonov P S.Theory of Impulsive Differential Equations [M].Singapore: World Scientific Publishing Company,1989.

[2] Anokhin A,Berezansky L,Braverman E.Exponential Stability of Linear Delay Impulsive Differential Equations [J].Journal of Mathematical Analysis and Applications,1995,193(3): 923-941.

[3] Berezansky L,Braverman E.Exponential Boundedness of Solutions for Impulsive Delay Differential Equations [J].Applied Mathematics Letters,1996,9(6): 91-95.

[4] Berezansky L,Braverman E.On Oscillation of a Second Order Impulsive Linear Delay Differential Equation [J].Journal of Mathematical Analysis and Applications,1999,233(1): 276-300.

[5] DING Wei,HAN Mao-an.Periodic Boundary Value Problem for the Second Order Impulsive Functional Differential Equations [J].Applied Mathematics and Computation,2004,155(3): 709-726.

[6] LIANG Rui-xi,SHEN Jian-hua.Periodic Boundary Value Problem for Second-Order Impulsive Functional Differential Equations [J].Applied Mathematics and Computation,2007,193(2): 560-571.

[7] Franco D,Nieto J J.First-Order Impulsive Ordinary Differential Equations with Anti-periodic and Nonlinear Boundary Conditions [J].Nonlinear Analysis: Theory Methods &Applications,2000,42(2): 163-174.

[8] Nieto J J.Basic Theory for Nonresonance Impulsive Periodic Problems of First Order [J].Journal of Mathematical Analysis and Applications,1997,205(2): 423-433.

[9] Nieto J J.Periodic Boundary Value Problems for First-Order Impulsive Ordinary Differential Equations [J].Nonlinear Analysis: Theory,Methods &Applications,2002,51(7): 1223-1232.

[10] Jankowski T,Lakshmikantham V.Monotone Iterations for Differential Equations with a Parameter [J].Journal of Applied Mathematics and Stochastic Analysis,1997,10(3): 273-278.

[11] Feckan M.Parametrized Singular Boundary Value Problem [J].Journal of Mathematical Analysis and Applications,1994,188(2): 417-425.

[12] Stanek S.On a Class of Functial Boundary Value Problems for the Equationx″=f(t,x,x′,x″,λ) [J].Ann Polon Math,1994,59(1): 225-237.

[13] Jankowski T.Monotone Iterations for First Order Differential Equations with a Parameter [J].Acta Mathematica Hungarica,1999,84(1/2): 65-80.

[14] ZHANG Feng-qin,MA Zhi-en,Jurang Y.Boundary Value Problems for First Order Impulsive Delay Differential Equations with a Parameter [J].Journal of Mathematical Analysis and Applications,2004,290(1): 213-223.

[15] ZHANG Yu.Robust Exponential Stability of Uncertain Impulsive Delay Difference Equations with Continuous Time [J].Journal of the Franklin Institute,2011,348(8): 1965-1982.

[16] XU Deng-guo,HUANG Ying,LIANG Lin.Existence of Positive Periodic Solution of an Impulsive Delay Fishing Model [J].Bull Math Anal Appl,2011,3(2): 89-94.

[17] LI Xiao-di,Bohner M.An Impulsive Delay Differential Inequality and Applications [J].Computers &Mathematics with Applications,2012,64(6): 1875-1881.