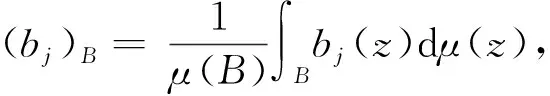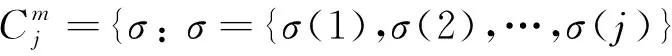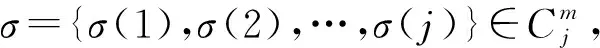齊型空間上帶非光滑核的奇異積分算子構成的多線性交換子的Lipschitz估計
孫愛文,陳 紅,束立生
(安徽師范大學 數學計算機科學學院,安徽 蕪湖 241003)
0 引 言
Rn上的奇異積分算子及其交換子是調和分析研究的主要內容. 自Duong等[1]給出帶非光滑核的奇異積分算子的定義及Pérez等[2]給出多線性交換子的定義以來,關于帶非光滑核的奇異積分算子生成的多線性交換子的研究已取得許多結果[3-10]. 本文討論帶非光滑核的奇異積分算子T與函數b(b∈Lipβ)生成的多線性交換子,得到了其是從Lp(X)到Lq(X)有界的.
定義1[3]設X是一個集合,在X上賦予一個正則的Borel測度μ及一個擬距離d. 對于d,存在常數kd≥1,使得?x,y,z∈X,有d(x,y)≤kd(d(x,z)+d(z,y));若μ滿足雙倍條件,即存在常數C≥1,使得?x∈X和r>0,有μ(B(x,2r))≤Cμ(B(x,r))<∞,其中B(x,r)表示以x為中心、r為半徑的擬球. 則稱(X,d,μ)是一個Coifman-Weiss意義下的齊型空間.
由于齊型空間上的μ滿足雙倍條件,因此有如下性質[4]:
1) 存在常數C>0,γ≥1,齊型空間的維數n,使得μ(B(x,γr))≤Cγnμ(B(x,r));
2) 存在常數C和N(0≤N≤n),使得
μ(B(y,r))≤C(1+d(x,y)/r)Nμ(B(x,r)), ?x,y∈X,r>0.
(1)
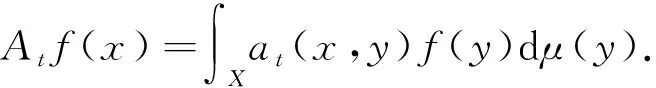
|at(x,y)|≤ht(x,y)=(μ(B(x,t1/δ)))-1·s(d(x,y)δt-1),
其中:δ是大于零的常數;s是一個正的有界遞減函數,且滿足:
(2)
這里的0<ε<1. 則稱一族算子{At}t>0為“廣義恒等逼近”.
定義3[6]如果算子T在L2(X)上有界,且存在核K(x,y),使得
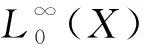
1) 存在“廣義恒等逼近”{Bt}t>0,使得TBt是以kt(x,y)為核的算子,T-TBt是以K(x,y)-kt(x,y)為核的算子,并且存在常數c1,ρ>0,使得該核滿足
2) 存在“廣義恒等逼近”{At}t>0,使得AtT是以Kt(x,y)為核的算子,T-AtT是以K(x,y)-Kt(x,y)為核的算子,且該核滿足
|Kt(x,y)|≤c2(μ(B(x,t1/δ)))-1,d(x,y)≤c3t1/δ,
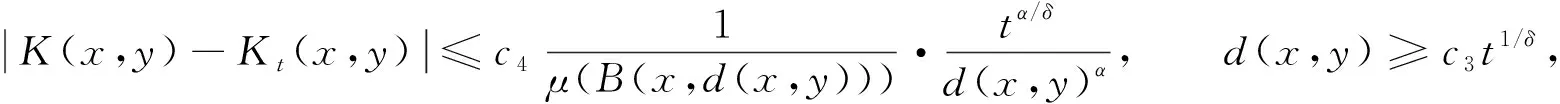
(3)
這里α>0.
定義4[7]設(X,d,μ)是一個齊型空間,0<β<1,齊型空間上的Lipschitz空間定義為
設b=(b1,b2,…,bm),bj∈Lipβ(j=1,2,…,m)為X上固定的局部可積函數,則由帶非光滑核的奇異積分算子T和b生成的多線性交換子定義為
本文出現的常數C>0,在不同之處表示不同的值.
1 引 理
引理1[1]1 引理2[8]對0<β<1,1≤r≤∞,令 設r ‖Mβ,r(f)‖Lq≤C‖f‖Lp. 引理3[9]對0<β<1,1≤p≤∞,有 引理4[10]假設B1?B2,f∈ Lipβ(X),則|fB1-fB2|≤C‖f‖Lipβμ(B2)β,其中B1,B2均為齊型空間上的擬球. 引理5令{At}t>0為“廣義恒等逼近”,0<β<1,b∈Lipβ(X),1≤p≤∞. 則對一切f∈Lp(X)和x∈X,有: 證明:1) 設f∈Lp(X),1≤p≤∞,對任意的x∈X,B為包含x的任意擬球,則 先估計Ⅰ. 通過式(1),可得μ(B)≤C2Nμ(B(x,rB)),對于任意的x∈B,如果x∈B,y∈2B,則有 因此,由引理3和引理4,可得 對于Ⅱ,x∈B,y∈2k+1B2kB,則d(x,y)≥2k-1rB,由齊型空間的性質,有 類似于Ⅰ的估計,有Ⅱ≤C‖b‖LipβMβ,1(f)(x). 綜合Ⅰ,Ⅱ的估計,1)得證. 同理,可以證2). 定理1設0<β<1/m,1 因此 對于J1(x),應用引理2及引理3,有 對于J2(x),固定1 對于J7(x),由式(3)及μ的雙倍條件,有 因此 綜上估計,有 由引理2及T在Lp(X)上的有界性,有 [1] Duong X T,Mcintosh A. Singular Integral Operators with Non-smooth Kernel on Irregular Domains [J]. Rev Mat Iberoamericana,1999,15(2): 233-265. [2] Pérez C,Trujillo-Gonzlez R. Sharp Weighted Estimates for Multilinear Commutators [J]. J London Math Soc,2002,65(3): 672-692. [3] HU Guo-en,WANG Wei-hong. A Weighted Estimate for the Maximal Commutators on Space of Homogeneous Type [J]. Acta Mathematica Sinica: Chinese Series,2010,53(1): 141-152. (胡國恩,王衛紅. 齊型空間上極大交換子的一個加權估計 [J]. 數學學報: 中文版,2010,53(1): 141-152.) [4] Coifman R,Weiss G. Analyse Harmonique Non-commutative Sur Certains Espaces Homognes [M]. Lecture Notes in Math. New York: Springer,1971: 242. [5] Duong X T,YAN Li-xin. Commutators of BMO Functions and Singular Integral Operators with Non-smooth Kernels [J]. Bull Austral Math Soc,2003,67(2): 187-200. [6] XU Jing-shi. Multilinear Commutators of Singular Integral Operators with Non-smooth Kernels [J]. Taiwanese Journal of Mathematics,2007,11(2): 483-496. [7] Pérez C. Endpoint Estimates for Commutators of Singular Integral Operators [J]. J Func Anal,1995,128(1): 163-185. [8] ZHANG Qian,LIU Lan-zhe. A GoodλEstimate for Multilinear Commutator of Singular Integral on Spaces of Homogeneous Type [J]. Armenian Journal of Mathematics,2010,3(3): 105-126. [9] Paluszynski M. Characterization of the Besov Spaces via the Commutator Operator of Coifman,Rochbeg and Weiss [J]. Indiana Univ Math J,1995,44(1): 1-17. [10] Genebashvili I,Gogatishvili A,Kokilashvili V,et al. Weighted Theory for Integral Transforms on Space of Homogeneous Type [M]. Longman: Piman Monogr and Survey in Pure and Appl Math,1998.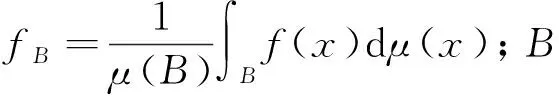
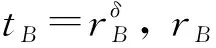
2 主要結果