實結合代數的雙環(huán)與Clifford代數的結構

張桂穎,李武明,張慶成

(1. 通化師范學院 數學學院,吉林 通化 134002;2. 東北師范大學 數學與統計學院,長春 130024)

Clifford代數在數學與物理學領域應用廣泛[1-8]. 本文由實結合代數的雙環(huán)討論p+q維Minkowski空間[3-4]Rp,q生成的Clifford代數Clp,q的性質. 結果表明: 非可除的Clp,q均存在雙環(huán)為其子代數;中心子代數非可除的Clp,q均為雙環(huán).

1 預備知識

有限維可結合的實可除代數均為Clp,q的子代數. 事實上,有限維可除的實可除結合代數只有R?Cl0,0,C?Cl0,1,H?Cl0,2. 除上述情形外,Clifford代數Clp,q均是非可除代數.

Clifford代數[3-4]Clp,q的生成空間Rp,q存在一組基:e1,…,ep,ep+1,…,ep+q,對Clifford積及Minkowski內積[5-7]滿足如下關系式:

由(p,q)型Minkowski空間 Rp,q生成的Clifford代數Clp,q的一組基為:

1;e1,e2,…,ep+q;e1e2,e1e3,…,e1ep+q,e2e3,…,e2ep+q,…,ep+q-1ep+q;…;e1e2…ep+q.

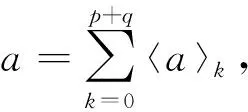
Clp,q的中心子代數[10]Cen(Clp,q)只可能是R?Cl0,0,C?Cl0,1,H?Cl1,0. 且有

(3)

其中H={a+bj|a,b∈R,j?R,j2=1}是 R上二維可交換的實結合代數,稱為雙曲復數,j稱為H的雙曲虛單位.

2 Clp,q有雙環(huán)為其子代數的條件

定義1設A為域F上的代數,利用A的加法運算與乘法運算,在A2={(a1,a2)|a1,a2∈A}上定義加法運算與乘法運算為(a1,a2)+(b1,b2)=(a1+b1,a2+b2)和(a1,a2)(b1,b2)=(a1b1,a2b2). 則A2構成環(huán),稱其為A的雙環(huán),記為2A.

若將A2視為F-線性空間,則2A還是F上的代數. 本文討論的雙環(huán)均為有限維實可除代數的雙環(huán).

例1實數域上雙環(huán)2R={(a,b)|a,b∈R},其單位元為(1,1),2R的零因子集為

Z(2R)={a(1,0)}∪{b(0,1)}.

例2實2階矩陣雙環(huán)2R(2)={(A,B)|A,B∈R(2)},且有

(A,B)∈Z(2R(2)) ?A∈Z(R(2))或B∈Z(R(2)).

例3四元數雙環(huán)2H={(α,β)|α,β∈H},其零因子集可表示為Z(2H)={α(1,0)}∪{β(0,1)}.

定理1設Clp,q是由p+q維Minkowski空間 Rp,q生成的Clifford代數,則Clp,q有子代數同構于雙環(huán)2R的充要條件是Clp,q是非可除的.

證明: 若Clp,q有子代數與雙環(huán)2R同構,即與雙曲數H同構,則Clp,q有雙曲虛單位,即Clp,q有非平凡自逆元. 若Clp,q有非平凡的自逆元u,u2=1,即u為Clp,q的一個雙曲虛單位,則Clp,q有子代數{a+bu|a,b∈R}?H?2R. 因此Clp,q有子代數與雙環(huán)2R同構等價于Clp,q有非平凡自逆元.

設u是Clp,q的一個非平凡自逆元,令v=(1+u)/2,則

即v是Clp,q的非平凡冪等元. 設v是Clp,q的非平凡冪等元,則存在非零元1-v,使得v(1-v)=0,即Clp,q有非平凡零因子.

由Clp,q是非可除的,Clp,q有非平凡零因子,可知p>0或q>2. 當p>0時,Clp,q有非平凡自逆元e1,命題成立. 當p=0時,必有q>2,Clp,q有三次單位向量e123為其非平凡自逆元. 證畢.

由定理1的證明過程,可得:

推論1Clp,q有子代數同構于雙環(huán)2R等價于Clp,q有非平凡的冪等元,且等價于Clp,q有非平凡的自逆元.

利用Clp,q中心子代數Cen(Clp,q)的表達式(3)及定理1的結論,可得:

定理2設Cen(Clp,q)是Clp,q的中心子代數,則Cen(Clp,q)有雙環(huán)結構的充要條件是Cen(Clp,q)非可除.

推論2Cen(Clp,q)有雙環(huán)結構等價于Cen(Clp,q)有非平凡的冪等元,且等價于Cen(Clp,q)有非平凡的自逆元.

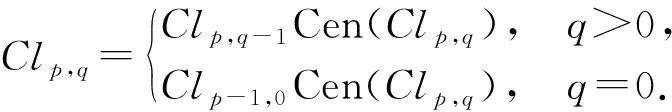
證明: 若Cen(Clp,q)有雙環(huán)結構,則必有p+q>0. 當q>0時,由定理2知

Cen(Clp,q)={a+be12…(p+q)|a,b∈R}.

任取a∈Clp,q,a可表示為

其中b,c∈Clp,q-1(?Clp,q). 故命題成立. 類似可證,q=0時命題也成立.

定理4若Clp,q的中心子代數Cen(Clp,q)有雙環(huán)結構,則Clp,q有雙環(huán)結構. 且

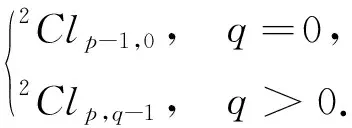
證明: 若Clp,q的中心子代數Cen(Clp,q)有雙環(huán)結構,則有

Cen(Clp,q)={a+be12…(p+q)|a,b∈R}?H?2R.

當q>0時,任取a∈Clp,q-1,b∈Cen(Clp,q),有: 1)ab=ba;2)Clp,q=Clp,q-1Cen(Clp,q);3) dimClp,q=2p+q=2p+q-1·2=dimClp,q-1dim Cen(Clp,q). 從而有Clp,q?Clp,q-1?Cen(Clp,q)?Clp,q-1?2R?2Clp,q-1. 同理可證,當q=0時,有Clp,q?2Clp-1,0,故命題成立.

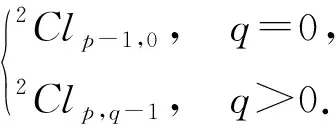
[1] Lounesto P. Clifford Algebra and Spinors [M]. New York: Cambridge University Press,2001.

[2] Doran C,Lasenby A. Geometric Algebra for Physicists [M]. New York: Cambridge University Press,2003.

[3] YANG Hai-quan. Clifford Algebra and Automated Geometric Theorem Proving [D]. Changchun: Jilin University,1998. (楊海圈. Clifford代數與幾何定理機器證明 [D]. 長春: 吉林大學,1998.)

[4] QIAO Yu-ying,YANG He-ju,LI Xiao-ling. Some Properties fork-Biregular Function in Clifford Analysis [J]. Advances in Mathematics (China),2012(2): 187-198.

[5] LI Wu-ming,ZHANG Qing-cheng. The Four-Dimensional Hyperbolic Complex Space Lorentz Group [J]. Journal of Northeast Normal University: Natural Science Edition,2005,37(2): 15-17. (李武明,張慶成. 四維雙曲復空間與Lorentz群 [J]. 東北師大學報: 自然科學版,2005,37(2): 15-17.)

[6] LI Wu-ming. Clifford Algebra and Minkowski Space Properties [J]. Acta Scientiarum Naturalium Universitatis Jilinensis,2000(4): 13-16. (李武明. Clifford代數與Minkowski空間的性質 [J]. 吉林大學自然科學學報,2000(4): 13-16.)

[7] LI Wu-ming,ZHANG Xue-feng. Clifford Algebra of Spacetime Plane and Abel Complex Number System [J]. Journal of Jilin University: Science Edition,2007,45(5): 748-752. (李武明,張雪峰. 時空平面的Clifford代數與Abel復數系統 [J]. 吉林大學學報: 理學版,2007,45(5): 748-752.)

[8] CAO Wen-sheng. Similarity and Consimilarity of Elements in 4-Dimensional Clifford Algebra [J]. Acta Mathematica Scientia,2010,30A(2): 531-541. (曹文勝. 四維Clifford代數的相似與合相似 [J]. 數學物理學報,2010,30A(2): 531-541.)

[9] Gallier J. Clifford Algebra,Clifford Groups,and a Generalization of the Guaternions: The Pin and Spin Groups [M]. New York: Cambridge University Press,2009.

[10] SONG Yuan-feng,LI Wu-ming,DING Bao-xia. The Central Subalgebra of Clifford AlgebraClp,q[J]. Journal of Tonghua Normal University,2011,32(12): 4-5. (宋元鳳,李武明,丁寶霞. Clifford代數Clp,q的中心子代數 [J]. 通化師范學院學報,2011,32(12): 4-5.)