帶有時變不確定性連續時間Takagi-Sugeno模糊系統的穩定性判據
李麗芳,孟慶元, 張 友
(1. 吉林警察學院 信息技術系,長春 130117;2. 吉林交通職業技術學院,長春 130012;3. 東北師范大學 計算機科學與信息技術學院,長春 130117)
非線性特性是工業系統中常見的物理特征,研究非線性系統的穩定性分析和控制設計問題具有重要的理論和應用價值. Takagi-Sugeno(T-S)模糊模型[1]成功解決了非線性系統的建模問題,王立新等[2]證明了T-S模糊模型能以任意精度逼近定義在緊集上的連續非線性函數,從理論分析上賦予了T-S模糊模型進行非線性系統建模的合法性. 在早期基于T-S模糊模型的非線性系統穩定性分析研究中,均采用單Lyapunov函數系統穩定性條件設計,但由于這種單Lyapunov函數對于所有的模糊子系統使用一個單一的Lyapunov矩陣,因此得到的系統穩定性條件保守性較大,從而限制了T-S模糊模型在非線性系統穩定性分析領域內的應用[3-8]. 為減少所得穩定性條件的保守性,文獻[4]提出了一種附件變量引入技術以減少穩定性判據的保守性. 文獻[5-8]對上述附加變量引入技術進行了改進,但由于單Lyapunov函數本身固有的缺點,因此很難在本質上對穩定性結果的保守性進行改善,因而要進一步減少保守性就必須使用新的Lyapunov函數. 文獻[9]提出了一種模糊Lyapunov函數,它能考慮更多關于模糊隸屬函數的有用信息,顯著減少了結果的保守性. 在此基礎上,文獻[10-14]也給出了基于模糊Lyapunov函數的模糊系統穩定性分析結果.
本文針對帶有時變不確定性連續時間T-S模糊系統的穩定性分析問題,提出一種新的基于線性矩陣不等式(LMI)形式的穩定性判據. 為實現減少已有穩定性判據保守性的目標,設計了兩種附加變量引入方法,使得在系統穩定性分析過程中能更有效地考慮模糊隸屬函數的有用信息. 在此基礎上,結合文獻[15-16]的結果得到了比已有方法保守性更小的穩定性判據. 特別地,相關的已有結果可視為本文結果的一種特例.
1 預備知識
考慮如下由r條模糊規則描述的帶有時變不確定性的連續時間T-S模糊系統[1]:如果ξ1(t)=M1i,…,ξp(t)=Mpi,則
(1)
其中:x(t)∈Rn為n維系統狀態向量;ξ1(t),ξ2(t),…,ξp(t)為模糊模型前件變量;Mij(i=1,2,…,p;j=1,2,…,r)為模糊集;Ai∈Rn×n為模糊模型已知參數矩陣;ΔAi為模糊模型未知時變不確定參數矩陣,且滿足如下范數有界條件:
ΔAi(t)=DF(t)Ei,FT(t)F(t)≤I, ?t≥0;
(2)
其中:D和Ei為已知適當維數矩陣;F(t)為未知矩陣值函數.
根據T-S模糊推理方法,系統(1)的總體模糊模型可表示為
(3)
在已有采用模糊Lyapunov函數進行系統穩定性分析中,試圖通過考慮模糊隸屬函數隨時間的導數信息減少所得穩定性判據的保守性,且常使用如下關于模糊隸屬函數導數的假設條件.
假設1對于帶有時變不確定性的連續時間T-S模糊系統(3),假設其模糊隸屬函數的導數變換界滿足如下條件[14]:
?ξ(t), 1≤i≤r,
(4)
這里λi為模糊建模時確定的實數.
文獻[10-14]給出了假設條件(4)在實際應用中的可獲取性,并給出了具體問題φi的幾種計算方法.
引理1[15]對于給定適當維數的矩陣Q=QT,H,E;滿足FT(t)F(t)≤I(?t≥0)條件的不等式Q+HF(t)E+(HF(t)E)T<0成立的充分必要條件是存在大于零的實數λ,使得
Q+λHHT+λ-1ETE<0
成立.

2 主要結果
為進一步減少已有基于模糊Lyapunov函數的不確定性T-S模糊系統穩定性判據的保守性,本文提出兩種新的附加變量引入技術,將各模糊子系統間的相互耦合關系映射到一個增廣大矩陣中,進而更有效地考慮模糊隸屬函數的有用信息,以獲得保守性更小的穩定性判據.
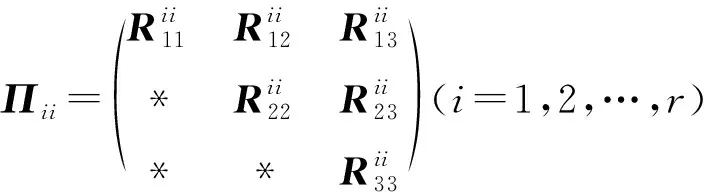
Pi+X>0,i=1,2,…,r;
(5)

(6)
(7)
(8)
其中:
則系統(3)是全局漸近穩定的.
證明: 為方便,下面證明中用x,hi代替x(t),hi(ξ(t)). 對系統(3)考慮如下模糊Lyapunov函數:
(9)
將V(x)沿系統(3)求時間導數可得
(10)
(11)
由式(11)可推出,若如下不等式成立,則系統(3)是全局漸近穩定的:
(12)
由式(2)可得
(13)

對式(13)使用引理1可得
(DF(t)E(t))TP(t)+P(t)DF(t)E(t)≤λ-1P(t)D(P(t)D)T+λE(t)(E(t))T.
(14)
于是,由式(12)~(14)可得系統(3)全局漸近穩定的充分條件是
(15)
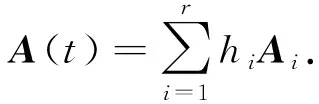
進一步,由引理2可得矩陣不等式(15)等價于如下矩陣不等式:
(16)

將不等式(16)的左側項進行重新編排,可得
(17)
此時,由不等式(6),(7)可得
若不等式(8)成立,則式(16)也成立,即帶有時變不確定性的連續時間T-S模糊系統(3)是全局漸近穩定的.

3 仿真實驗
考慮如下帶有時變不確定性的連續時間T-S模糊系統:
(19)
系統(19)的矩陣參數為
ΔAi(t)=DF(t)Ei,i=1,2,3,4;
其中可變系統參數α用于比較定理1與已有文獻結果間的保守性強弱關系.
下面使用Matlab的LMI工具計算在相同條件下,分別利用定理1和文獻[14]的相應結果進行求解可變系統參數α的穩定區域范圍. 這里,將假設1中的參數設定為φi=-2.6(i=1,2,3,4). 此時,用文獻[14]相應結果計算的帶有時變不確定性連續時間T-S模糊系統的穩定區域為α<160,而由本文方法計算的相應穩定區域為α<190. 可見,本文方法的系統穩定區域大于文獻[14]的系統穩定區域,即本文所提出的穩定性判據具有更小的保守性.
選擇α=160,該點在文獻[14]的系統穩定判據中是不穩定點,但在本文的定理1中是穩定點,即只有使用定理1才能保證系統在α=160時是全局漸近穩定的.
給定系統初始值為x(0)=(1.6,-1.4)T,圖1給出了系統(19)當α=160時狀態軌跡隨時間的變化曲線. 圖2給出了系統(19)當α=160時兩個狀態x1(t)和x2(t)由初始狀態點(1.6,-1.4)漸近趨向零點的變化軌跡. 由圖1和圖2可見,當初始條件為x(0)=(1.6,-1.4)T時,系統(19)在α=160處是漸近穩定的.

圖1 當x(0)=(1.6,-1.4)T時系統 狀態隨時間的變化軌跡Fig.1 Trajectories of system state variation with time when x(0)=(1.6,-1.4)T

圖2 當x(0)=(1.6,-1.4)T時系統 狀態漸近趨向零點的軌跡Fig.2 Convergent trajectory of system state variation when x(0)=(1.6,-1.4)T
給定系統初始值為x(0)=(-0.8,0.6)T,圖3給出了系統(19)當α=160時狀態軌跡隨時間的變化曲線. 圖4給出了系統(19)當α=160時兩個狀態x1(t)和x2(t)由初始狀態點(-0.8,0.6)漸近趨向零點的變化軌跡. 由圖3和圖4可見,當初始條件為x(0)=(-0.8,0.6)T時,系統(19)在α=160處也是漸近穩定的.

圖3 當x(0)=(-0.8,0.6)T時系統 狀態隨時間的變化軌跡Fig.3 Trajectories of system state variation with time when x(0)=(-0.8,0.6)T

圖4 當x(0)=(-0.8,0.6)T時系統 狀態漸近趨向零點的軌跡Fig.4 Convergent trajectory of system state variation when x(0)=(-0.8,0.6)T
綜上所述,本文給出了一種帶有時變不確定性連續時間T-S模糊系統的穩定性新判據. 通過提出兩種新的附加變量引入技術,在充分考慮模糊隸屬函數的代數特性基礎上,將各模糊子系統間的相互耦合關系映射到一個增廣大矩陣,能顯著減少所得系統穩定性判據的保守性. 由仿真實驗結果可見,本文所提方法與已有結果相比具有更小的保守性.
[1] Takagi T,Sugeno M. Fuzzy Identification of Systems and Its Application to Modeling and Control [J]. IEEE Transactions on Syst Man Cybern,1985,15(1): 116-132.
[2] WANG Li-xin,Mendel J M. Fuzzy Basis Functions,Universal Approximation,and Orthogonal Least-Squares Learning [J]. IEEE Transactions on Neural Networks,1992,3(5): 807-814.
[3] Tanaka K,Ikeda T,Wang H O. Fuzzy Regulators and Fuzzy Observers: Relaxed Conditions and LMI-Based Designs [J]. IEEE Transactions on Fuzzy Systems,1998,6(2): 250-265.
[4] Kim E,Lee H. New Approaches to Relaxed Quadratic Stability Conditions of Fuzzy Systems [J]. IEEE Transactions on Fuzzy Systems,2000,8(5): 523-534.
[5] LIU Xiao-dong,ZHANG Qing-ling. New Approaches toH∞Controller Designs Based on Fuzzy Observers for T-S Fuzzy Systems via LMI [J]. Automatica,2003,39(9): 1571-1582.
[6] Sala A,Arino C. Asymptotically Necessary and Sufficient Conditions for Stability and Performance in Fuzzy Control [J]. Fuzzy Sets and Syetms,2007,158(24): 2671-2686.
[7] Sala A,Arino C. Relaxed Stability and Performance Conditions for T-S Fuzzy Systems with Knowledge on Membership Function Overlap [J]. IEEE Transactions on Syst Man Cybern: Part B,2007,37(3): 727-732.
[8] Montagner V F,Oliveira R,Peres P. Convergent LMI Relaxations for Quadratic Stabilizability andH∞Control of Takagi-Sugeno Fuzzy Systems [J]. IEEE Transactions on Fuzzy Systems,2009,17(4): 863-873.
[9] Tanaka K,Ohtake H,Wang H O. A Descriptor System Approach to Fuzzy Control System Design via Fuzzy Lyapunov Functions [J]. IEEE Transactions on Fuzzy Systems,2007,15(3): 333-341.
[10] Lam H K,Leung F H F. LMI-Based Stability and Performance Conditions for Continuous-Time Nonlinear Systems in Takagi-Sugeno’s Form [J]. IEEE Transactions on Syst Man Cybern: Part B,2007,37(5): 1396-1406.
[11] Lam H K. Stability Analysis of T-S Fuzzy Control Systems Using Parameter-Dependent Lyapunov Functions [J]. IET Control Theory and Applications,2009,3(6): 750-762.
[12] ZHANG Hua-guang,XIE Xiang-peng. Relaxed Stability Conditions for Continuous-Time T-S Fuzzy-Control System via Augmented Multi-indexed Matrix Approach [J]. IEEE Transactions on Fuzzy Systems,2011,19(3): 478-492.
[13] Tognetti E S,Oliveira R C L F,Peres P C. SelectiveH2andH∞Stabilization of Takagi-Sugeno Fuzzy Systems [J]. IEEE Transactions on Fuzzy Systems,2011,19(5): 890-900.
[14] Mozeli L A,Palhares R M,Souza F O,et al. Reducing Conservativeness in Recent Stability Conditions of T-S Fuzzy Systems [J]. Automatica,2009,45(6): 1580-1583.
[15] Petersen I R,Hollot C V. A Riccati Equation to the Stabilization of Uncertain Linear Systems [J]. Automatica,1986,22(4): 397-411.
[16] Boyd S,Ghaoui L E,Feron E. Linear Matrix Ineuqalities in System and Control Theory [M]. Philadelphia: Society for Industrial Mathematics,1997.

