簡單半序約束下多個正態總體分布參數的Bayes估計與等值檢驗

史海芳, 姬永剛

(1. 吉林大學 數學研究所, 長春 130012; 2. 中國民航大學 理學院, 天津 300300)

0 引 言

考慮單向方差分析模型：

yij=μi+ij,j=1,2,…,ni,i=1,2,…,k.

(1)

其中: 響應變量yij表示第i種試驗第j個個體的值;μi為第i種試驗的平均值; 隨機誤差ij為相互獨立的服從正態分布N(0,σ2)的隨機變量.

在很多實際問題中, 通過一些先驗信息可知總體均值滿足一定的序約束. 如簡單半序μ1≤…≤μk, 簡單樹半序μ1≤μi(i=2,3,…,k), 傘型半序μ1≤…≤μp≥μp+1≥…≥μk等. 文獻[1-2]給了在這些先驗信息下一些感興趣參數的估計和檢驗. 此外, 文獻[3-5]分別考慮了構造總體均值置信區間的問題. 進一步, 文獻[6]介紹了用U-I(union-intersection)檢驗法考慮似然比檢驗統計量的精確分布, 通過計算p值, 解決了簡單半序約束下的檢驗問題. 但上述的頻率方法在理論上一般較復雜, 實際操作不太方便. 因此, 近年人們試圖從Bayes角度考慮序約束下的估計和檢驗問題, 如文獻[7-8]分別用Bayes方法考慮了如下等值檢驗問題:

H0:μ1=…=μkv.s.H1:μ1≤…≤μk,μ1<μk;

(2)

的估計, 同時考慮了如下等值檢驗問題:

(3)

最后用Gibbs抽樣和Metropolis-Hastings方法給出了數值模擬. 與非Bayes方法相比, Bayes方法在處理中、 小樣本問題時具有很大優勢. 特別地, 如果拒絕原假設, 根據Bayes方法還可以知道哪些總體均值和標準差之比是不同的.

1 Bayes分層模型

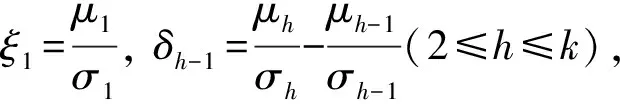
[δhρh,θh]=ρhI(δh=0)+(1-ρh)g(δhθh)I(δh>0),h=1,2,…,k-1,

(4)

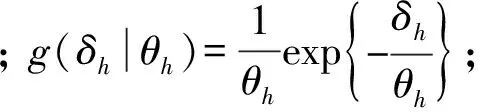
(5)

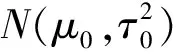
綜上, Bayes分層模型為:

2 滿條件后驗分布

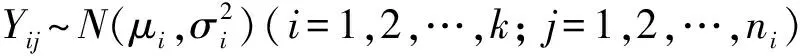
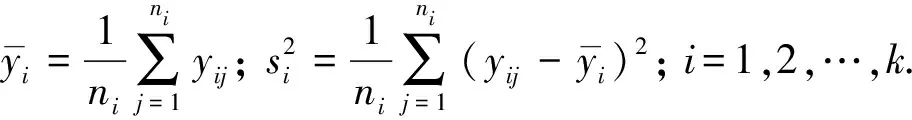
由Bayes分層模型知, 所有未知參數包括δj,ρj,θj,ξ1,σi(j=1,2,…,k-1;i=1,2,…,k).

2.1 δj的滿條件后驗分布

由Bayes公式知

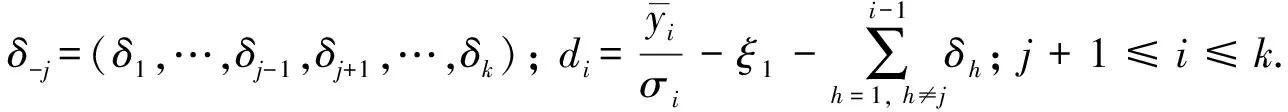
因此, 給定y,{σi},ρj,θj,ξ1,δ-j下,δj的滿條件后驗分布是一個混合分布:

其中

(7)

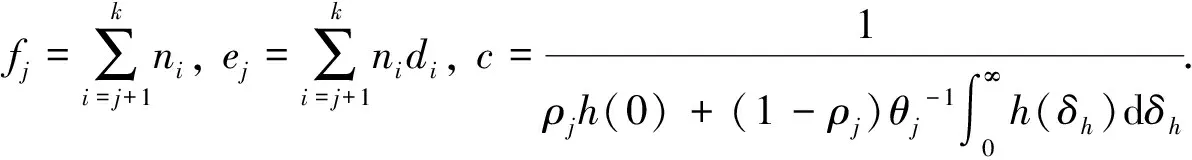
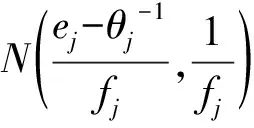
2.2 ξ1的滿條件后驗分布

由Bayes公式知

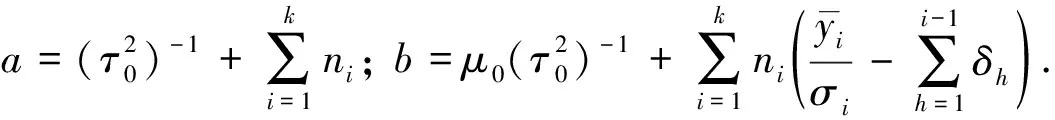
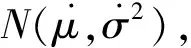
2.3 ρi的滿條件后驗分布

由Bayes公式知

ρi的滿條件后驗分布可以記作

當α0=β0=1時, 有

2.4 θi的滿條件后驗分布

由Bayes公式知

θi的滿條件后驗分布可以記作

2.5 σi的滿條件后驗分布

由Bayes公式, 有

顯然,σi的滿條件后驗不是一個常見分布, 所以本文用Metropolis-Hastings方法給出σi的數值模擬.

3 數值模擬

3.1 Gibbs抽樣

Gibbs抽樣步驟如下：

2) ① 先通過下式計算fj和ej:

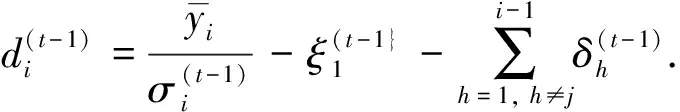
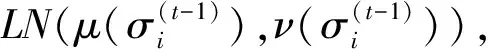
(8)

解方程組(8)得

② 計算r.

③ 從(0,1)上的均勻分布抽取一隨機數u:

3.2 數值模擬

下面通過數值模擬檢驗本文的方法. 考慮總體個數k=4時的情況, 已知δj=μj+1/σj+1-μj/σj,j=1,2,3. 共模擬4組總體. 為方便, 令每組總體中均值和標準差比的間隔δj都分別相等, 分別為0.5,0.75,1,1.25. 因此產生如下4組數據:

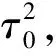
表1 不同樣本數下檢驗問題(3)的勢

表2～表4分別列出了一次抽樣中參數的估計值和δj=0的后驗概率, 其中Bayes估計是本文方法給出的估計, Frequentist估計是利用文獻[10]中頻率方法得到的參數估計值. 由表2可見, 對于參數δ1,δ2和δ3, 當n=30,100時, 本文方法都給出了比頻率方法更精確的估計. 盡管當n=30時, 頻率方法給出的參數ξ估計值比本文方法更接近真值, 但當n=100 時, 本文方法給出的估計值更接近真值. 由表3可見, 本文方法給出的參數ξ,δ1,δ3估計值優于頻率方法給出的估計值, 但對于參數δ2, 頻率方法給出了比本文方法更精確的估計. 由表4可見, 只有參數δ1當n=30時和參數δ3當n=100時, 頻率方法優于本文方法, 其他情況都是本文方法優于頻率方法. 總之, 兩種方法給出的估計值類似, 都與真值很接近. 對于檢驗問題(3), 從表中數據可見應用本文給出的Bayes方法得到的結果較理想. 其中在表3中, 盡管當間隔δj較小且樣本量不大(n=30)時出現了與實際不符的檢驗結果(P(δ2=0Y)=0.611 7), 但隨著樣本的增多或間隔的增大(表4), 從后驗概率都小于0.5易見4個正態總體均值與標準差比都不同. 這主要是由于間隔較小時很難正確識別出所有不同的均值和標準差的比.

表2 當μ=(1,1,1,1), σ=(1,1,1,1)時一次抽樣中參數的估計值和δj=0的后驗概率

表3 當μ=(0,1,2,3), σ=(1,1,1,1)時一次抽樣中參數的估計值和δj=0的后驗概率

表4 當μ=(0,2,4,6), σ=(1,1,1,1)時一次抽樣中參數的估計值和δj=0的后驗概率

進一步, 當原假設成立時, 本文對犯第一類錯誤的概率進行了模擬, 結果列于表5. 考慮4組總體, 數據按如下總體產生:

其中σ=(σ1,σ2,σ3,σ4)分別取(1,1,1,1),(3,3,3,3),(6,6,6,6),(10,10,10,10).

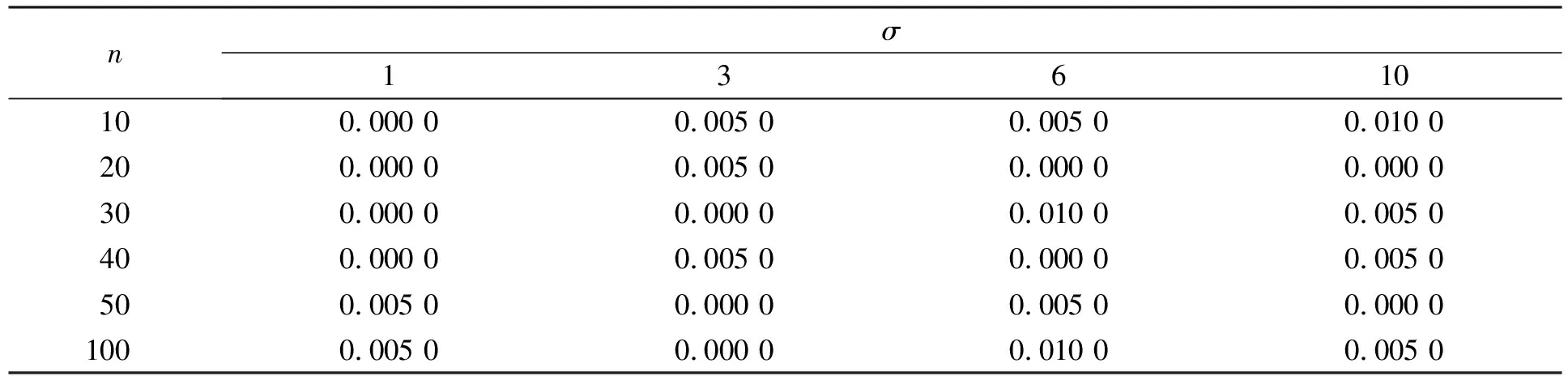
表5 不同樣本數和方差下犯第一類錯誤的概率

由表5可見, 本文方法能很好地控制犯第一類錯誤的概率, 甚至當標準差很大(σ=10)時, 犯第一類錯誤的概率仍然很小, 因此本文方法是一個相對保守的方法. 此外, 在表5中, 當σ=(1,1,1,1)時似乎隨著樣本量的增加犯第一類錯誤的概率也增加, 為了檢驗這一結論本文做了很多模擬, 結果顯示當n=49時, 犯第一類錯誤的概率為0.005 0, 當n=60,70,80,90,110,120時, 犯第一類錯誤的概率均為0, 因此, 并不存在犯第一類錯誤的概率隨樣本量增加而增大的趨勢. 當間隔δ不是太小時, 本文的Bayes方法在處理檢驗問題(3)時, 在控制犯第一類錯誤很小的同時, 也能達到一個合理的檢驗勢.

[1] Robertson T, Wright F T, Dykstra R L. Order Restricted Statistical Inference [M]. New Jersey: John Wiley & Sons Inc, 1988.

[2] Silvapulle M J, Sen P K. Constrained Statistical Inference: Inequality, Order and Shape Restrictions [M]. New Jersey: John Wiley & Sons Inc, 2005.

[3] Hayter A J. A One-Sided Studentized Range Test for Testing against a Simple Order Alternative [J]. Journal of the American Statistical Association, 1990, 85(411): 778-785.

[4] LIU Lin. Simultaneous Statistical Inference for Monotone Dose-Response Means [D]. Newfoundlan: Memorial Universtiy of Newfoundland, 2001.

[5] LIU Lin, Lee C C, PENG Jian-an. Max-Min Multiple Comparison Procedure for Isotonic Dose-Response Curves [J]. Journal of Statistical Planning and Inference, 2002, 107(1/2): 133-141.

[6] 史寧中. 統計檢驗的理論與方法 [M]. 北京: 科學出版社, 2008.

[7] SHANG Jun-feng, Cavanaugh J E, Wright F T. A Bayesian Multiple Comparison Procedure for Order-Restricted Mixed Models [J]. International Statistical Review, 2008, 76(2): 268-284.

[8] Oh M S, Shin D W. A Unified Bayesian Inference on Treatment Means with Order Constraints [J]. Computational Statistics & Data Analysis, 2011, 55(1): 924-934.

[9] Chou Y M, Owen D B. A Likelihood Ratio Test for the Equality of Proportions of Two Normal Populations [J]. Communications in Statistics: Theory and Methods, 1991, 20(8): 2357-2374.

[10] LI Shu-you, SHI Ning-zhong, ZHANG Bao-xue. Testing Ratios of Means to Standard Deviations from Normal Populations under Order Restrictions with Generalizedp-Values [J]. Chinese Journal of Applied Probability and Statistics, 2009, 25(1): 77-85. (李樹有, 史寧中, 張寶學. 正態總體均值與標準差比在序約束下的廣義p-值檢驗 [J]. 應用概率統計, 2009, 25(1): 77-85.)