車用液壓緩沖器動態特性研究
馬星國,顧婷婷,尤小梅
(沈陽理工大學機械工程學院,遼寧沈陽110159)
履帶車輛常用的行程限位裝置為彈性限制器和液壓緩沖器[1]。與彈性限制器通過彈性元件變形來儲存和釋放能量的工作方式相比,液壓緩沖器是利用液體通過小孔和縫隙時,將沖擊能量轉化為熱能耗散掉。液壓緩沖器可以消除二次振動現象,有效地限制負重輪的動行程,改善車輛的行駛平穩性,因此在懸掛系統中有比較大的作用[2]。
目前,德國的豹2A1 到豹2A6 等坦克均采用了液壓緩沖器[3]。液壓緩沖器的研究主要集中在將計算機仿真技術應用在緩沖器的設計中,理論上取得了很多成果。但如何與實際更好地結合,得到更好的緩沖性能仍是有待解決的問題。
作者在研究緩沖器的緩沖作用機制的基礎上,建立了動態緩沖過程的數學模型,進行動態仿真計算,并對影響液壓緩沖器動態特性的因數進行了分析。
1 液壓緩沖器的特性分析
緩沖器主要由承壓件、緩沖件(介質)、復位件及殼體等四部分構成。其基本作用原理如下:沖擊載荷作用于承壓導桿時,導桿帶動活塞推動流體運動,利用流體流過節流孔和活塞與缸壁間縫隙所產生的阻尼效應,吸收并耗散沖擊動能;待沖擊物移去時,復位件的彈性能使承壓導桿回復至沖擊前的初始位置。
所研究的液壓緩沖器在緩沖過程是由3 個節流孔和球面縫隙共同作用產生緩沖力來抵抗沖擊載荷。作者分析了節流孔阻尼特性和球面縫隙流阻尼特性以及油液的壓縮特性,來研究緩沖器的綜合特性。
1.1 節流孔的流量
文中研究的液壓緩沖器在導桿的頂端徑向均勻分布3 個節流孔,孔的尺寸符合薄壁小孔條件,即通過節流孔的流量為:


式中:Cd為流量系數,A 為3 個小孔的流量面積,Δp 為活塞兩側的壓力差,ρ 為液壓油密度。
1.2 球面縫隙流流量
活塞運動過程中,油液在球面活塞與缸壁之間的流動稱為壓差-剪切流,含兩種方式的油液流動,體現的是一種聯合流動[4]。
1.2.1 壓差流
實際工程中,由于制造、裝配等原因致使油缸和活塞都處于圖1 所示的偏心工作狀態,且緩沖器常常工作在側向力很大的狀況下,因此在研究縫隙流時,須考慮球面活塞的偏心與偏轉。

圖1 活塞與缸壁位置關系俯視圖
圖1中h 為β 角處的間隙高度,e 為偏心距,R1為活塞球面半徑,R2為缸壁半徑。設h0=R1-R2為活塞和缸壁同心時的間隙高度,ε =e/h0為相對偏心率,得出h ≈h0+ (1 +εcosβ)。
圖2 為考慮活塞偏轉情況,活塞與缸壁的關系視圖,油液從活塞與缸壁之間的縫隙流過。由圖2 可知:

其中:α 為活塞的偏轉角,L 為活塞厚度的一半,γ1,2為微通道方法的積分限[5]。

圖2 活塞與缸壁位置關系側視圖
圖2 中的每一條微通道都是一個寬度極小的由弧面與平面構成的流通道。對于每一條微通道,運用微積分原理及斜面縫隙的分析方式進行分析[6]。
把每一條微通道的縫隙視為無數微小的dx 的累加,則壓差流為:

在全長內,對x 進行積分,代入l = cosγR2+ h,經過計算推導可以得到球面縫隙壓差流量:

其中:

1.2.2 剪切流
對于剪切流,同樣可利用微通道原理進行研究,由剪切流公式[4]可得微通道剪切流量為:
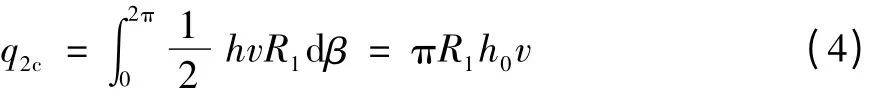
由此可得活塞與缸壁之間的壓差-剪切縫隙總流量q2:

1.3 油液可壓縮特性
油液的可壓縮性是流體承受壓力變化時其體積發生變化的屬性,以體積彈性系數Ke來表示,其定義公式為:

式中:V 為上腔油液體積,緩沖過程中,下腔壓強變化較小,認為p2保持不變,可推出:設上腔的初始體積為V0,可得活塞的行程x 與V 的關系式
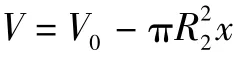

綜合以上,可得緩沖器的油液流量連續方程為
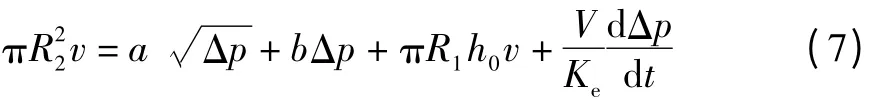
假設活塞運動速度v 保持恒值,可認為Δp 保持不變,由式(6)可知dV/dt=0。得到液壓緩沖器的綜合特性,如下式:

式中:q=πR22v-πR1h0v
取相應的設計參數代入式(8)得出緩沖器的綜合特性曲線(壓差-速度關系),圖3 為特性曲線隨著節流口節流面積變化的曲線,節流面積由直徑d 表示。可見壓差隨著速度的增大而增大。低速時,節流孔的節流阻尼作用明顯,表現薄壁小孔的二次特性;高速時,縫隙流起主要作用,表現球面縫隙的一次特性;再隨著節流面積的增大,薄壁小孔的二次特性愈加明顯,曲線在低速階段表現出明顯的非線性特征。

圖3 活塞速度-壓差曲線
2 緩沖過程的建模及仿真
2.1 數學模型的建立
圖4 為緩沖器的結構示意圖,沖擊載荷為質量m 的沖擊塊,沖擊塊撞擊緩沖器活塞頭的速度為

圖4 緩沖器結構示意圖
設活塞的行程和速度分別為x 和v,可建立活塞力的平衡方程:

式中:m 為沖擊質量;A1= πR21為上腔油液壓力面積;A2=πR21-πR23為下腔油液壓力面積,R3為導桿半徑;p1=p2+Δp;K 為復位彈簧剛度;y0為彈簧預壓縮量。
由式(7)可以得到Δp 的微分方程,由式(9)可以得到v 的微分方程,x 的微分方程式為v。綜合以上可得到緩沖過程的微分方程組如下:

補充方程緩沖力F=m·dv/dt
2.2 仿真計算
運用四階龍格-庫塔數值方法解微分方程組,在計算機上使用MATLAB 語言編寫仿真程序,從而實現緩沖過程的動態模擬仿真[8]。其仿真計算的流程如圖5 所示。

圖5 仿真計算流程圖
3 仿真結果及分析
3.1 仿真計算結果
緩沖器的主要結構參數如下:h0= 0.16 mm,d=4 mm,R1= 32.34 mm,R2= 32.5 mm,R3= 25 mm;設定初始值Δp=0,x=0,v=1 m/s。經計算得到x,v,Δp 隨時間的變化曲線如圖6—8 所示。

圖6 行程-時間曲線

圖7 速度-時間曲線

圖8 壓差-時間曲線
3.2 緩沖器動態特性分析
緩沖器的動態特性曲線一般由緩沖力F 隨緩沖行程x 變化曲線來表示,如圖9 所示。曲線所包含的面積即為緩沖器所吸收的能量,曲線越接近矩形,在相同的緩沖能量下,緩沖力越小,緩沖效果越好。

圖9 緩沖力-行程曲線
從圖6、圖7、圖9 可知:活塞t=0.07 s 時速度由1 m/s 迅速減小到0.4 m/s 左右,走過了約0.04 m(占總行程的50%);在前50%的行程中,耗時0.07 s,僅占總用時的23.3%,吸收了大部分的能量(占總能量的70%左右),而后半程盡管耗時較長、但吸收能量很小,說明緩沖器后半程作用發揮得不好。因此,緩沖力-行程曲線的后半程有待優化。
3.2.1 沖擊工況對緩沖特性的影響
沖擊初速度v 和沖擊質量m 對緩沖特性的影響如圖10、圖11 所示。當沖擊質量一定時,隨著沖擊速度的增加緩沖力峰值明顯增大;當沖擊速度一定時,隨著沖擊質量的增加,緩沖力峰值增加較小。緩沖器吸收的能量為E0=1/2mv2,因為速度在二次項,因此對緩沖能量的影響要比沖擊質量更明顯。

圖10 沖擊初速度對緩沖力的影響

圖11 沖擊質量對緩沖力的影響
3.2.2 結構及介質對緩沖特性的影響
圖12 為節流孔直徑對緩沖特性的影響曲線。可知:當沖擊載荷一定時,隨著直徑的增大,緩沖力峰值變小,緩沖行程變大。
圖13 為活塞與缸壁的縫隙不同時的緩沖力曲線。可知:當沖擊載荷一定時,活塞與缸壁的縫隙h0對緩沖特性的影響最大,決定了緩沖曲線的形狀。當h0較小時,緩沖力上升較快,峰值過高,行程較短,起不到應有的緩沖效果。當h0較大時,緩沖力峰值較小,速度降低緩慢,行程較大,甚至可能出現在緩沖行程內沒有完全吸收沖擊能量導致撞缸的現象,因此設計合理的縫隙大小對緩沖器的緩沖效果至關重要。

圖12 節流孔直徑對緩沖性能的影響

圖13 球面縫隙對緩沖性能的影響
油液作為緩沖介質,其體積彈性模量Ke對緩沖特性的影響如圖14 所示,當沖擊載荷一定時,Ke值越大,油液的壓縮性越差,油液的剛度越大,碰撞時緩沖力迅速達到峰值,曲線波動較大。適當減少Ke,可以降低緩沖力峰值,減少剛性沖擊,且緩沖吸收能量基本不變。

圖14 體積彈性模量對緩沖性能的影響
4 結論
(1)從文中的緩沖器結構看,節流孔的阻尼在低速緩沖時起主要作用,球面縫隙阻尼在高速緩沖起主要作用。h0決定球面縫隙的一次特性,h0過小時,如側向力過大可能會造成卡死現象,h0過大則起不到足夠的緩沖作用。合理選擇h0的值對緩沖效果至關重要。
(2)油液的壓縮對緩沖吸能貢獻很小,但適當地減少Ke值,可以改善緩沖性能。
(3)緩沖器的工作與緩沖初速度和緩沖質量相關,其中緩沖初速度對最大緩沖力影響較大,緩沖質量對最大緩沖力影響很小。
【1】王書鎮.高速履帶車輛行駛系[M].北京:北京工業學院出版社,1986.
【2】丁法乾.履帶式裝甲車輛懸掛系統動力學[M].北京:國防工業出版社,2004.
【3】鄭慕僑,馮崇植,藍祖佑.坦克裝甲車[M].北京:北京理工大學出版社,2003.
【4】金朝銘. 液壓流體力學[M]. 北京:國防工業出版社,2000.
【5】張文斌,周曉軍.越野車用液壓緩沖器的特性分析及其影響參數研究[J].中國機械工程,2008,19(12):1415 -1418.
【6】張宇.液壓緩沖器研究及其對車輛動力學性能的研究[D].北京:北京理工大學,2003.
【7】譚宗柒,汪云峰,陳永清.阻尼孔連續型液壓緩沖器研究及設計[J].起重運輸機械,2008(2):27 -29.
【8】姜健飛.數值分析及其MATLAB 實驗[M]. 北京:科學出版社,2004.

