數控車削加工切削參數優化

范有雄，吳元祥，陳金牛

(1. 武漢軟件工程職業學院，湖北武漢4200205;2. 武漢東風楚凱汽車零部件有限公司，湖北武漢430015)

汽車產業不斷壯大，汽車零件的生產加工企業間的競爭也日益激烈。圖1 所示零件是小型汽車用于轉向部的后懸臂軸零件， 生產批量大，外圓表面硬度HRC59，幾何形狀精度要求高。通過工藝論證，并進行工藝試驗，探討了使用基于CBN 刀具的硬車削加工工藝替代傳統的磨削加工工藝過程。

圖1 后懸臂軸

基于CBN 刀具的硬態車削加工在機械加工應用中一直處于探索試用階段，沒有全面取代傳統的工藝方法，一方面是由于產品質量的控制與穩定，另一方面，加工效率是否能比傳統的磨削加工效率高，生產效率能提高的幅度有多大。因此應用硬態車削加工技術需要做好工藝分析、論證與試驗工作，在確保產品質量的前提下，優化數控車削加工參數，提高生產率，降低工藝成本。

1 優化目標確定

產品零件加工制造系統是由與生產相關的各子系統組成，生產制造系統的優化是按照整個系統設定的目標函數為最優來確定各子系統參數，這樣的系統稱為最優化系統。對于金屬切削機械制造系統，金屬切削加工各個環節對整個系統有著密切影響，所以應力求產品的整個制造過程的優化，也就是從毛坯制造、零件加工到產品裝配的全過程優化。但是由于技術上的困難，建立產品制造全過程全環節的優化理論模型比較復雜，另一方面要進行整體優化分析需要企業產品制造及管理中的大量數據，同時實現整體優化需要過高的費用，周期較長，因此對機械加工系統的優化分析重點放放各個子系統的優化而達到整個系統的優化。

機械加工系統的優化通常分為5 級，第1 級為單工序(即每臺機床構成的工藝系統)加工條件的優化。第2 級為多工序加工條件的優化。這兩級是一個優化值的計算問題，是整個機械加工系統優化的基礎。第3 級是各臺機床負荷的優化，第4 級是使用機床種類和數量的優化，第5 級為各種零件加工序排列的優化，后3 級屬于管鋰范圍。1 ～5 級構成了整個加工系統的最優化。當然，對于產品制造企業來說，優化的對象還包括其他方面的子系統，如產品批量投放等其他管理系統的優化。

根據不同的需求，機械加工系統的優化目標不同。評價系統優化的指標有產品切削加工時間、產品質量、零件加工工藝成本、產品利潤等。系統的優化是以產品質量為前提，高效為目標，以達到產品制造的優質、高效、低成本的目標。工序的優化是基礎，切削加工時間是工序優化的主要目標值，加工時間影響著生產率、產品制造工藝成本等。因此確定數控車削加工工序優化的目標即為工序加工時間。

2 數學模型的建立

2.1 優化參數的確定

經過前面的分析，確定了以數控車削工序加工時間作為優化的目標，因此需要建立一個與工序加工時間相關的目標函數。

對于金屬切削加工工藝系統，在確定了加工對象、刀具、裝夾、機床的前提下，決定工序加工時間的一般參數為切削用量三要素，即切削速度v、進給量fr、切削深ap。在實踐中，不同的加工階段選擇不同的控制參數，粗加工階段，以提高加工效率為主要目的，通常對只控制一個參數(ap或fr)，精加工階段，主要考慮加工質量下的高效率，需要同時控制兩個參數v 和fr或3 個參數v、fr、ap。

數控車削加工工序的優化還會受到其他因素的影響，如材料性能的變化、工藝系統的動態特性、刀具磨損、熱變形等。這些隨機因素往往會影響最優工作的條件，為此，加工過程中還要采取實時監控的方式，及時調整，保持系統的穩定性。

2.2 基本數學模型的建立

確定最優車削用量三要素的最佳組合，必須建立以v、fr、ap為函數形式的目標函數t = g (v，fr，ap)，工序時間是研究機械加工效率、生產成本的基本要素，因此確立工序單件加工時間與三要素的關系，從而分析滿足目標要求的最佳數控加工參數。

(1)單件生產時間(min/件)

式中:Tm為工序時間(min/件)，切除金屬余量所耗費的機動時間;Tkx為空行程時間(min/件);Tct為刀具磨鈍后更換刀具、調整、對刀所需時間 (min/次);T 為刀具耐用度(min);Tqt為切削加工所需的輔助時間(如卸刀，裝刀，對刀，切削過程中的換刀時間，加工準備時間，操作者生理需要時間等)(min/件)。

在數控車削加工中，設定工件的切削走刀長度為lw(mm)，切入切出行程 l0(mm)，主軸轉速nw(r/min)，工件直徑 dw(mm)，每轉進給量fr(mm/r)，快速走刀量f0(mm/min)，平均每刀切削深度ap(mm)，工件余量為Δ(mm)。

因此可得切除當前工序余量所需機動時間:

式中:l=lw+l0。

在加工對象確定的條件下，切削長度、加工直徑是確定值，令:

單件基本時間可表示成fr、v、ap的函數式:

切削加工中空行程時間與數控車床設定快速移動速度(G00)及退刀行程有關，一般來說，退刀行程與切削行程相差ltd(5 ～10 mm)，因而工序空行程時間為:

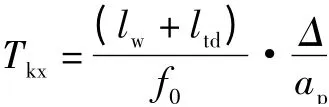
根據切削原理，廣義的刀具耐用度可以用下式表述:

式中:x0、y0、z0、C0為常數，與刀具、工件材料及工序切削加工條件有關。

將式(3)— (5)代入式(1)得:

則式(6)可改寫為:

式(7)表明了工序時間是v、fr、ap的函數。

將式(7)分別對v、fr、ap求偏導，并令其等于零，可求出函數式在無約束條件下的最小值，即時間最短下的切削用量三要素:

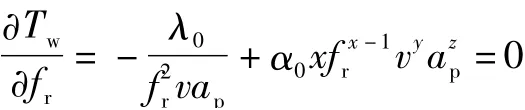
即

即

即

式(8)— (10)顯示:v、fr、ap→∞時，Tw值將無限減小，因而利用式(7)在無約束條件下不可能求出一組具有實際生產意義的切削用量三要素，所以切削加工工序參數的優化需要考慮工藝系統的具體制造約束條件。

2.3 約束條件

機械車削加工工藝系統在實際實施中受到較多條件的限制，如機床主軸的最高轉速、刀具能承受的最高切削速度、工藝系統的剛性、加工工件的表面粗糙度要求等。

(1)速度約束條件

vmin和vmax分別是由工件直徑和機床上最低、最高主軸轉速決定的最低和最高切削速度。

(2)進給速度約束條件

frmin和frmax分別是車削加工過程中限定的最低和最高進給速度。

(3)工件表面粗糙度約束條件

式中:rε為刀具的刀尖圓弧半徑(mm);

Rmin為工件允許的表面最大不平度(mm)。

由上式可求得一個滿足表面粗糙度的最小進給量

根據約束條件(11)和(12)得:

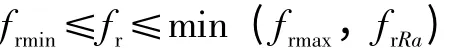
(4)功率約束條件

按切削力經驗公式計算出切削功率

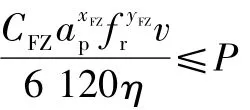
式中:CFZ、xFZ、yFZ分別為主切削力經驗系數與指數，與切削材料等有關系;

η 為材料的單位切削抗力(N/mm2);

P 為機床主電機功率(kW)。

為說明問題方便，假設fmin=0，vmin=0，ap=0，

則上述約束條件可歸納為:

因此由式(7)及約束條件(13)— (16)建立了以車削加工工序時間為目標的優化切削參數模型。

3 參數優化計算方法

在有約束最優化問題中，通常要將該問題轉換為更簡單的子問題，這些子問題可以求解并作為迭代過程的基礎。除了早期的方法通常是通過構造懲罰函數等來將有約束的最優化問題轉換為無約束最優化問題進行求解外，現在，由于計算技術及軟件技術的發展，專家提出了更有效的基于K-T (Kuhn-Tucker)方程解的方法、模擬生物進化的變搜索域遺傳算法、模擬退火算法、粒子群優化算法等計算方法。

變搜索域遺傳算法，即在每代中，求得優化參數{x}的各變量xi及其在群體中適應值f≥0 的區域［ximin，ximax］，解碼后再根據此區域進行編碼。由于群體在整體上朝著最優的方向發展，使群體集中到適應值高的區域，因而［ximin，ximax］ 不斷縮小，搜索區域縮小則算法很快得到最優解。

模擬退火算法起源于對固體退火過程的模擬，是局部搜索算法的擴展，它不同于局部搜索之處是以一定的概率選擇領域中費用值大的狀態。從理論上分析，它是一個全局最優算法，主要通過采用Metmpolis 接受準則，并用一組冷卻進度表的參數控制算法進程，使算法在多項式時間里給出一個近似優化解，是一種適合于求解混合離散化問題和目標函數不可微的復雜非線性問題的隨機性方法，不僅接受使目標函數值變“好”的點，而且還能夠以一定概率接受使目標函數值變“差”的點，這種計算方法有利于避免搜索過程陷大局部最優解，可以有效地搜索到全局最優解。

進化算法是一類模仿生物進化的優化算法，主要包括遺傳算法(GA)、遺傳編程法(GP)、進化規劃法(EP)、進化策略法(ES)和模擬退火法 (SA)等，其運算過程與生物進化過程相仿。對優化問題無可微性和連續性要求，具有全局收斂性、通用性及魯棒性強等優點。

粒子群算法是一種進化算法，粒子群算法的優點是收斂速度快，但存在算法精度較低、易發散等缺點。和其他的優化算法相比，粒子群算法不僅具有全局尋優能力，而且編程簡單，易于推廣使用。建立的切削參數優化模型不一樣，相應地就有不同的優化方法。如在前面所提及的基于模糊粗糙集理論優化方法、極值法等。具體的算法請參考有關專著。

4 結束語

大批量汽車零件加工生產中，零件裝配互換性高，質量穩定性要求高。采用基于CBN 刀具的硬車削加工新工藝技術，通過合理優化切削加工參數v、fr、ap，降低工序加工時間，提高零件加工單班產量，降低工藝成本，優化工藝參數，能綜合提高綜合經濟效益。

【1】王愛玲.數控加工理論與使用技術［M］.北京:機械工業出版社，2009.

【2】周澤華. 金屬切削原理［M］. 上海:上海科技出版社，1984.

【3】顧崇銜.機械制造工藝學［M］.西安:陜西科學技術出版社，1986.

【4】何獻忠.優化技術及其應用［M］.北京:北京工業學院出版社，1986.

【5】應錦春. 現代設計方法［M］. 北京:機械工業出版社，2000.

【6】秦建華，李智.改進型粒子算法在數控加工參數優化中的應用［J］.組合機床及自動化加工，2005(5):9 －11.

【7】張雙德.基于改進型模擬退火算法的數控加工切削參數優化［J］.煤礦機械，2004(6):76 －78.

【8】武美萍，翟建軍，廖文和. 數控加工參數優化研究［J］.中國機械工程，2004(3):235 －237.

【9】申麗國，韓至駿，張昆.應用生物遺傳算法規劃切削參數［J］.中國機械工程，1994(6):34 －35.