典型細長體結構的兩點激勵振動試驗設計

陳 穎，田光明，鐘繼根

（中國工程物理研究院 總體工程研究所，綿陽 621900）

0 引言

在武器產品研制過程中，常需要開展細長體結構的振動試驗。傳統試驗中，通常采用單一振動臺，通過擴展臺面連接、多點平均控制的方式開展試驗，但是隨著多自由度振動控制技術的發展，越來越多的設計和試驗人員認識到可以采用多個振動臺協同試驗以模擬細長體結構的多點載荷激勵，提高試驗模擬的置信度[1-3]。本文分析了某典型細長體結構在傳統單軸振動試驗中存在的問題，并對該結構兩點激勵振動試驗方案、夾具、控制等的設計情況以及試驗結果進行了介紹。

1 單振動臺振動試驗方案分析

1.1 某典型細長體結構

某典型細長結構（如圖1所示）是一個直徑360 mm、長2400 mm、壁厚5 mm 的圓筒形結構，通過前、中、后3 個支撐框與外部平臺連接。

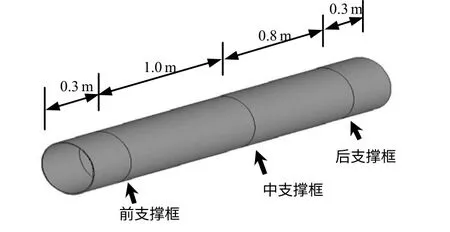
圖1 某典型細長結構示意圖Fig.1 Schematic diagram of a typical slender structure

3 個支撐框之間的距離分別為1000 mm 和 800 mm。前支撐框和其他兩個支撐框所受到的外部平臺傳遞過來的振動量級并不相同，分別為5.10g和4.16g，如圖2所示。

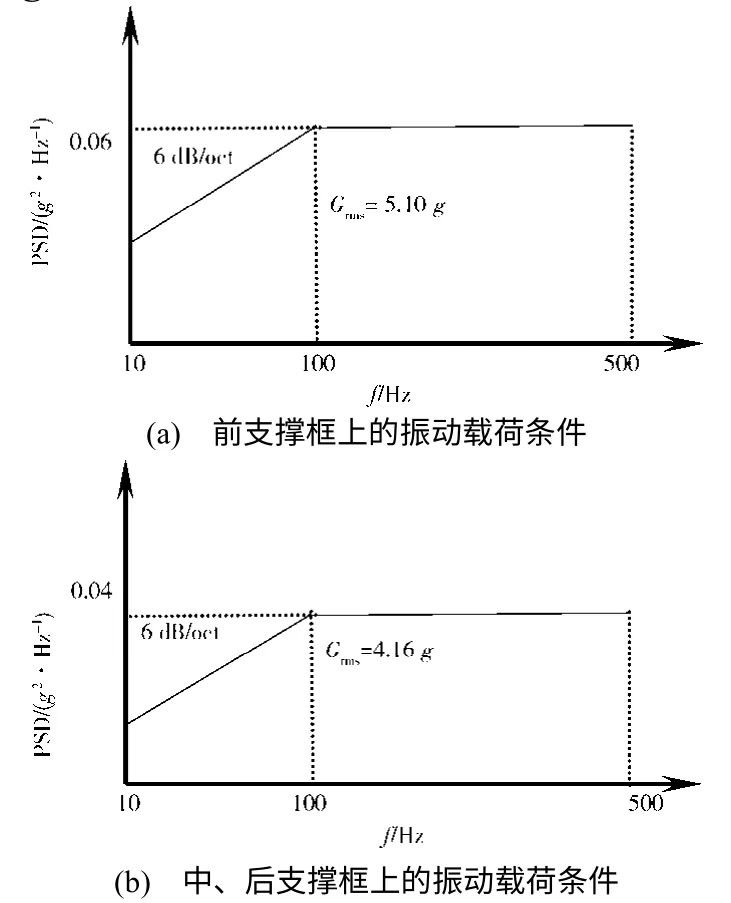
圖2 振動試驗的載荷條件Fig.2 Loading condition in vibration test

1.2 振動試驗效應分析

利用單振動臺進行加載時，只能施加一個載荷條件，因此一般是基于包絡的思想，按照量級高的振動試驗條件進行加載，所加的振動載荷條件如圖2(a)所示。這時產品的中、后支撐框承受的振動載荷比實際要大。

夾具設計時，根據實際的邊界條件，采用3 個支撐框固定的方式。由于結構尺寸長，因此夾具設計時考慮通過擴展臺面與振動臺進行連接（如圖3所示）。由于結構各部分質量分布不均勻，為保證質心過臺面中心，臺面兩邊的擴展夾具大小是不一致的。

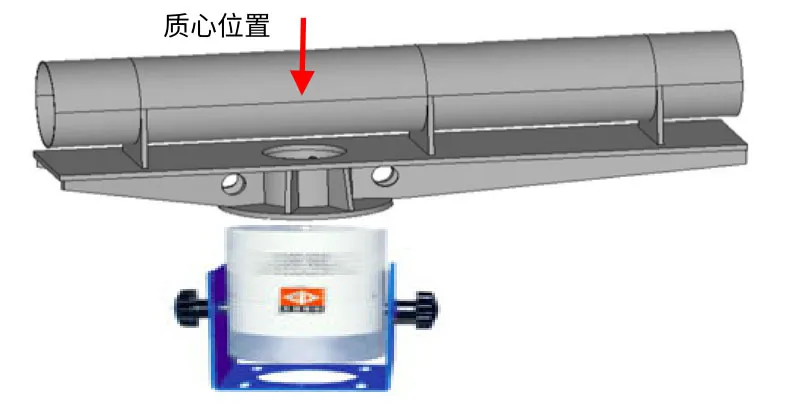
圖3 試件及夾具示意圖Fig.3 Schematic diagram of the test specimen and the fixture

對帶夾具的試件進行有限元分析（見圖4）。施加圖2(a)所示的基礎激勵載荷，即譜密度為 0.06g2/Hz 的載荷。圖5給出了3 個支撐框的加速度響應曲線。

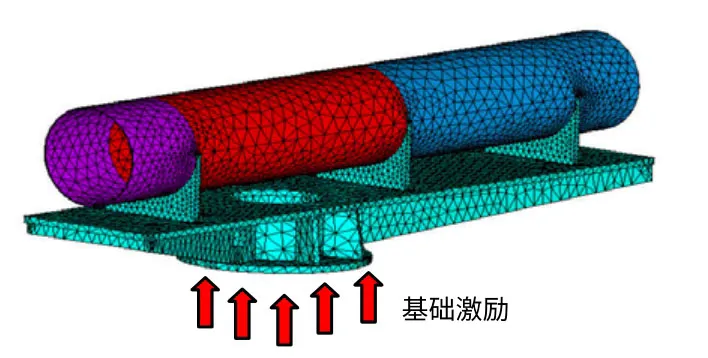
圖4 試件及夾具的有限元模型Fig.4 Finite element model of the test specimen and the fixture

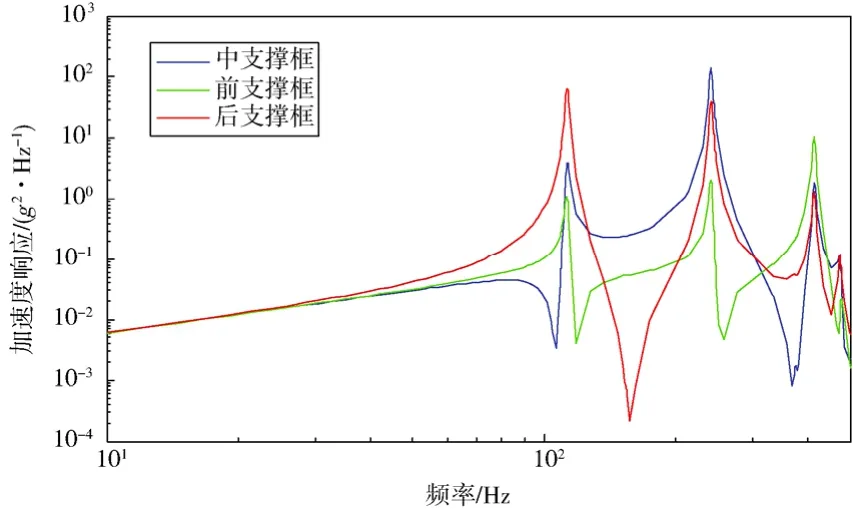
圖5 3 個支撐框的振動響應曲線Fig.5 Vibration response curves on the three supporting frames

從圖5可以看出：結構在不同部位的動力學特性是比較復雜的，3 個支撐框的動力學響應有較大的差異。而對于這種尺寸較大、響應較為復雜的試件，在試驗中一般采用多點平均控制方式，即在產品的3 個支撐框上分別布置3 個加速度控制點進行平均控制。圖5中，后支撐框（紅色曲線）的振動響應量級明顯比前支撐框（綠色曲線）要大，在多點平均控制時，如果平均譜達到圖2(a)所示的0.06g2/Hz的加速度譜，則后支撐框的實際響應會高于平均譜，而前支撐框的響應低于平均譜。由于后支撐框本來就施加了比真實載荷（0.04g2/Hz）要高的激勵，因此后支撐框附近在多點平均中被進一步過考核，而前支撐框附近則未達到需要的考核量級（0.06g2/Hz）。

因此，對于這種細長體結構，使用單振動臺來開展振動試驗，由于前后部位載荷條件的不同，以及擴展夾具和試件耦合的復雜動力學響應的不均勻性，使得試驗與真實環境有較大的差異，所以試驗宜采用雙振動臺的方式。

2 雙振動臺振動試驗設計

2.1 振動臺的選擇

最好選用兩個相同類型的振動臺進行細長體結構的振動試驗，這樣在夾具設計、試件安裝等方面都較為方便，但若實際條件不允許，則用兩個不同類型的振動臺組建試驗系統也是可行的。試驗前應根據結構質量在兩個振動臺上的分布，可采用公式(M1+M夾具1)×A1＜F1、(M2+M夾具2)×A2＜F2粗略估算振動臺的推力是否滿足要求，式中：M1、M2分別為試件分布在兩個振動臺上的質量，可根據試件和兩個振動臺之間的位置關系來分配；A1、A2分別為兩個振動臺所施加載荷條件的加速度總均方根值；F1、F2分別為兩個振動臺的推力。

本文采用了一個8 t 振動臺和一個6 t 振動臺組成的雙振動臺試驗系統。

2.2 夾具的設計

產品的前支撐框通過一個小的夾具1 與振動臺1 連接，中、后兩個支撐框的距離較近，振動量值一致，因此通過一個稍大的擴展夾具2 與振動臺2連接，如圖6所示。與圖3所示的大擴展夾具相比，夾具2 擴展部分的尺寸較小，剛度較好，因此中、后框上的動力學響應是比較接近的。

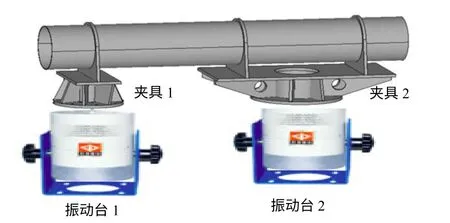
圖6 兩點激勵振動試驗夾具設計示意圖Fig.6 Fixture design in the dual-exciter vibration test

當選用不同類型的振動臺時，由于兩個振動臺的臺體高度往往會有所差異，因而在夾具設計中要注意兩個振動臺的高度匹配問題。可通過兩個夾具的高度差設計來使產品保持水平，以避免試件在支撐框處受到不必要的附加載荷。但是，由于試件在兩個振動臺上分布的質量不同，即使前期的設計中充分計算了夾具和振動臺的高度差，在試件裝上振動臺后，也會導致振動臺氣囊的下降程度不同并引起試件有輕微的傾斜，因此在試驗中可以準備不同厚度的墊片，以便將試件調平。如果振動臺對中可調，則更加方便試件調平。

在雙振動臺振動試驗中，兩個激勵點施加各自的隨機載荷，因而存在時域信號不同步的問題。其中一個振動臺動圈向上運動的時候，另一個振動臺動圈可能在向下運動，這將使得振動臺承受一定程度的偏載，可能造成振動臺能力的下降或動圈的損壞，因此，應在試驗前對兩個激振點的位移差、偏轉角度等進行計算分析。

對于圖2所示振動載荷條件，兩個激振點的位移總均方根值分別為：

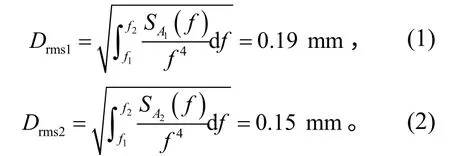
考慮隨機振動的3σ最大位移差（根據隨機振動理論，位移時域信號在3σ以內的概率為99.73%）為

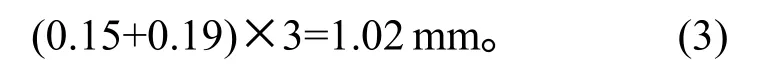
兩個振動臺中心距離為1415 mm，因此兩點3σ位移差引起的偏轉角度為

由此可見，上述條件引起的兩個振動臺的位移差和偏轉角度都很小，完全在振動臺的抗傾覆能力范圍內，因此夾具和臺面可以直接采用剛性連接。

當兩個振動臺的位移差和偏轉角度較大時，為了保護振動設備，一般不宜采用剛性連接的方式，這時可以考慮在振動臺和夾具之間安裝球鉸（見圖7）。 連接球鉸通常是一種液壓軸承裝置，應滿足以下兩個要求：一是能消除振動過程中的彎矩，二是能將高頻振動有效傳遞到試件上。國外的Team 公司以及國內的一些廠家都在研發類似的球鉸裝置。

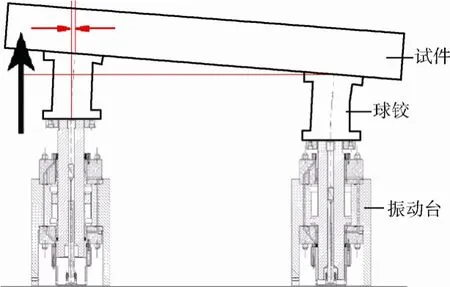
圖7 球鉸安裝示意圖Fig.7 Installation of the ball joints

由于球鉸具有自身特定的共振頻率，因此在使用了球鉸后，控制點應該位于球鉸上部，以保證試件經受規定的振動載荷。

2.3 試驗控制方式

采用多輸入多輸出控制方式[4-6]來施加兩點激勵隨機振動載荷，其載荷條件為

式中：對角線元素分別為兩個激振點的自功率譜密度；非對角元素表示兩個激振點之間的互功率譜密度。在試驗中不考慮互譜關系時，矩陣的非對角元素為0。

兩點激勵隨機振動控制原理如圖8所示。

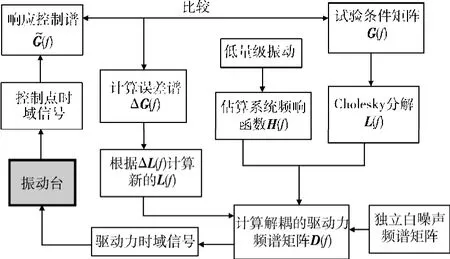
圖8 兩點激勵隨機振動試驗控制原理框圖Fig.8 The principle of the dual-exciter random vibration test control

控制步驟如下：

1）進行低振級試驗，獲取控制點的加速度時域響應信號；

2）通過快速傅里葉變換（FFT）計算兩點驅動與兩點響應的互功率譜密度以及驅動的自功率譜密度，并估算驅動與響應之間的頻響函數矩陣；

3）計算驅動力頻譜矩陣，通過快速傅里葉逆變換（IFFT）得到驅動信號，控制兩個振動臺進行驅動；

5）根據誤差譜重新計算驅動力頻譜矩陣，生成驅動信號重新對振動臺進行驅動。重復步驟4）～5），使振動控制在規定的容差范圍內。

3 結構的雙振動臺振動試驗

按照上述試驗設計，在中國工程物理研究院環境試驗中心開展了某細長結構的雙振動臺振動試驗。試驗狀態如圖9所示。

圖9 兩點激勵隨機振動試驗Fig.9 The dual-exciter random vibration test

控制點位置分別位于前支撐框和后支撐框上，圖10給出控制譜圖，可以看出：試驗控制效果良好，兩個點的隨機振動控制結果均優于±3 dB 容差要求。

圖10 兩點激勵振動試驗控制譜圖Fig.10 Control spectrum of the dual-exciter random vibration test

4 結束語

本文以某細長體結構為例，分析了采用傳統單振動臺開展試驗存在的問題。因其前后連接點激勵 載荷不同以及擴展夾具和試件耦合的復雜動力學響應的不均勻性，采用傳統的單點激勵方法容易造成過試驗或欠試驗，而采用雙振動臺方式的兩點激勵隨機振動試驗則可滿足試驗要求。本文對兩點激勵隨機振動試驗的參數估計、設備選型、夾具連接、控制方式等的研究可為開展類似細長體結構的振動試驗提供參考。

（References）

[1]Hamma G A, Stroud R C, Underwood M A.A review of multi-axis/multi-exciter vibration technology[J].Sound and Vibration, 1996, 30(4)∶20-27

[2]張正平, 王宇宏, 朱曦全.動力學綜合環境試驗技術現狀和發展[J].裝備環境工程, 2006, 3(4)∶7-11 Zhang Zhengping, Wang Yuhong, Zhu Xiquan.Current state and developing trend of combined dynamic environmental test[J].Equipment Environmental Engineering, 2006, 3(4)∶7-11

[3]樊世超, 馮咬齊.多維動力學環境模擬試驗技術研究[J].航天器環境工程, 2006, 23(1)∶23-28 Fan Shichao, Feng Yaoqi.Study on multi-DOF dynamic environment simulation technology[J].Spacecraft Environment Engineering, 2006, 23(1)∶23-28

[4]Stroud R C, Hamma G A.Multi-exciter and multi-axis vibration exciter control systems[J].Sound and Vibration, 1988, 22(4)∶18-28

[5]賀旭東, 陳懷海, 申凡, 等.雙振動臺隨機振動綜合控制研究[J].振動工程學報, 2006, 19(2)∶145-149 He Xudong, Chen Huaihai, Shen Fan, et al.Study on dual-shaker random vibration test control[J].Journal of Vibration Engineering, 2006, 19(2)∶145-149

[6]陳穎, 劉青林, 韓宇航, 等.多軸低頻隨機振動試驗控制方式研究[J].航天器環境工程, 2009, 26(6)∶523-527 Chen Ying, Liu Qinglin, Han Yuhang, et al.The control modes in multi-axial and low-frequency random vibration tests[J].Spacecraft Environment Engineering, 2009, 26(6)∶523-527