確定性測(cè)試矢量生成的低功耗設(shè)計(jì)

李 鵬，顏學(xué)龍，孫 元

(桂林電子科技大學(xué)電子工程與自動(dòng)化學(xué)院，廣西桂林541004)

隨著深亞微米工藝技術(shù)的發(fā)展，集成電路的工藝尺寸日益減少，電路節(jié)點(diǎn)的物理可訪問(wèn)性正逐步削弱以至于消失，這使得電路和芯片的測(cè)試變得尤為困難，以往依賴自動(dòng)測(cè)試儀器ATE(Automated Test Equipment)方法，因其傳輸帶寬和存儲(chǔ)容量的制約，已經(jīng)增加了大量測(cè)試成本。內(nèi)建自測(cè)試BIST(Built-in Self Test)擺脫了對(duì)昂貴ATE設(shè)備的依賴，僅僅依靠片上的資源完成對(duì)電路的測(cè)試［1-2］。傳統(tǒng)的內(nèi)測(cè)試方法如窮舉/偽窮舉測(cè)試、偽隨機(jī)測(cè)試、確定性測(cè)試等方法，在測(cè)試時(shí)間、故障覆蓋率、測(cè)試功耗和硬件開(kāi)銷等方面都值得改進(jìn)，許多學(xué)者針對(duì)測(cè)試矢量生成結(jié)構(gòu)的這些綜合因素提出了解決方案，如文獻(xiàn)［3-4］提出了一種低功耗DS-LFSR測(cè)試生成方案，方案不僅提高了故障覆蓋率，而且還降低了部分測(cè)試功耗;文獻(xiàn)［5］提出一種雙模式的低功耗LFSR結(jié)構(gòu)，該結(jié)構(gòu)在不降低故障覆蓋率的條件下，減少了超過(guò)70%的測(cè)試功耗;文獻(xiàn)［6-7］提出了一種矢量插入結(jié)構(gòu)，在保證一定故障覆蓋率的前提下，通過(guò)降低原有的矢量對(duì)間的漢明距離，來(lái)減少測(cè)試功耗;文獻(xiàn)［8］提出了一種基于格雷碼的電路自測(cè)試序列的分配算法，方案根據(jù)電路的基本輸入權(quán)重，合理分配格雷序列的跳變位，測(cè)試具有較高的故障覆蓋率，而且更大程度上降低了測(cè)試功耗。

本文提出一種基于確定性矢量的低功耗測(cè)試生成方案，通過(guò)可配置反饋網(wǎng)絡(luò)的LFSR來(lái)完成確定性測(cè)試矢量的生成，以保證有很高的故障覆蓋率，并通過(guò)外圍的單翻轉(zhuǎn)矢量的生成邏輯，在欲生成的確定性測(cè)試矢量間插入單一翻轉(zhuǎn)的測(cè)試矢量，以降低被測(cè)電路的各類功耗。對(duì)ISCAS’85基準(zhǔn)電路的實(shí)驗(yàn)結(jié)果表明:該測(cè)試方案能得到很高的故障覆蓋率，而且測(cè)試功耗降低明顯。

1 可配置反饋網(wǎng)絡(luò)的LFSR結(jié)構(gòu)

傳統(tǒng)的LFSR可以產(chǎn)生隨機(jī)性較好的測(cè)試矢量，然而這類矢量只能檢測(cè)出被測(cè)電路中的隨機(jī)矢量可測(cè)性故障(Random Pattern Detectable Faults)，而電路中的一部分抗隨機(jī)性故障(Random Pattern Resistant Faults)需要借助固定的算法，產(chǎn)生一些有針對(duì)性的矢量才能夠被檢測(cè)［9］。可配置反饋網(wǎng)絡(luò)的LFSR作為一種混合測(cè)試生成結(jié)構(gòu)，既能生成確定性測(cè)試矢量，又能生成偽隨機(jī)性測(cè)試矢量，本文正應(yīng)用了該結(jié)構(gòu)，以生成Atalanta工具模擬產(chǎn)生的一組確定性矢量集，以提高單位測(cè)試時(shí)間內(nèi)的故障覆蓋率。

1.1 確定性測(cè)試矢量的生成結(jié)構(gòu)

可配置反饋網(wǎng)絡(luò)的LFSR的結(jié)構(gòu)如圖1所示，各個(gè)觸發(fā)器的輸入是由觸發(fā)器輸出經(jīng)反饋異或配置和選擇反向器配置得到(合并稱“反饋配置”)。

圖1 可配置LFSR結(jié)構(gòu)

該電路的各個(gè)輸入Vi可用含有r個(gè)觸發(fā)器輸出的邏輯變量QL1(n)，QL2(n)，…，QLr(n)和反向配置邏輯變量Ci表示成二元域內(nèi)的線性非齊次方程:

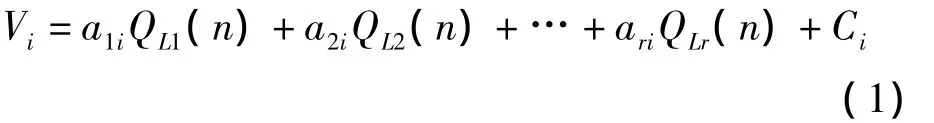
其中aki為第k個(gè)觸發(fā)器反饋接入第i位輸入Vi的配置節(jié)點(diǎn)，aki∈{0，1}，k、i=1，2，…，r.aki=1 時(shí)，表示反饋接入異或門，反之表示無(wú)反饋接入;Ci為非門控制，Ci∈{0，1}，Ci=1時(shí)表示通過(guò)非門接入輸入，反之則直通輸入;QLi為第i位觸發(fā)器輸出。如果按確定性測(cè)試矢量集的順序，將待生成的測(cè)試矢量的第i位從第1個(gè)序列到第s個(gè)序列依次代入到方程(1)中，即可得到矩陣方程(2)，這里的表示第i位的第x個(gè)測(cè)試序列的次態(tài)值，x=1，2，…，s并有=V(x+1)i。并記 CNi=(a1i，a2i，…，ari，Ci)為該位的反饋配置向量，對(duì)應(yīng)于式(2)中的各個(gè)部分，可簡(jiǎn)記為:b=A·CNi，其中b為確定性矢量在第i位的次態(tài)值，A中Vxi為確定性矢量的現(xiàn)態(tài)值，s為確定性測(cè)試集的大小。

如果方程(2)有解，說(shuō)明該確定性測(cè)試集的第i位序列可以完全通過(guò)反饋配置向量CNi得到;反之，說(shuō)明該反饋配置向量只能生成原確定性測(cè)試集在第i位中的一部分序列，而另一部分需要重新代入式(1)，構(gòu)造新的矩陣方程，尋求新的配置向量，直到全部測(cè)試集可解為止。故生成完整的確定性測(cè)試集，可能需要對(duì)原測(cè)試集進(jìn)行劃分，進(jìn)而得到多個(gè)反饋配置向量。

1.2 確定性測(cè)試矢量的劃分

圖2為多通道的可配置LFSR結(jié)構(gòu)，完整的確定性測(cè)試集被劃分為p個(gè)子集，而每個(gè)子集由相應(yīng)的配置向量作用一定的時(shí)鐘來(lái)生成，其中配置通道的個(gè)數(shù)和配置向量的作用時(shí)鐘都需要對(duì)原測(cè)試矢量的劃分來(lái)決定，矢量劃分的理論基礎(chǔ)，就是非齊次方程組的有解判定定理。

圖2 多通道的可配置LFSR結(jié)構(gòu)

定理1非齊次線性方程組

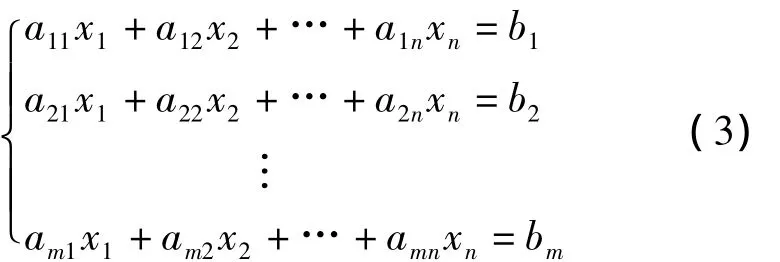
定理2設(shè)η是非齊次方程組的一個(gè)特解，ξ1，ξ2，…，ξn-r，是其導(dǎo)出組的基礎(chǔ)解系，則非齊次方程組(3)的通解為 η +k1ξ1+k2ξ2+ … +kn-rξn-r，其中r=R(A)，k1，k2，…，kn-r為任意常數(shù)。

推論若R(A)=R(A|b)=n時(shí)，方程組(3)有唯一解;若R(A)=R(A|b)＜n時(shí)，方程組(3)有無(wú)窮多解，其通解為 η +k1ξ1+k2ξ2+ … +kn-rξn-r;若R(A)≠R(A|b)時(shí)，方程組(3)無(wú)解。

根據(jù)上述的定理1和推論可知:方程組(3)中只有當(dāng)R(A)=R(A|b)時(shí)，才可以求出其配置向量CNi，若R(A)≠R(A|b)，則需要對(duì)原測(cè)試進(jìn)行劃分，劃分的步驟為:

(1)將方程組(2)中的增廣矩陣(A|b)，做行初等變換(二元域內(nèi)的模2加)，使每行第一個(gè)非零元素下面的數(shù)為0。

(2)找出增廣矩陣(A|b)中A陣全為0，而b中不為零的行，即使R(A)≠R(A|b)的行，那么該行即為原測(cè)試集的一個(gè)劃分點(diǎn)。

(3)將原測(cè)試集在該劃分點(diǎn)之后的測(cè)試矢量重新代入方程(2)，并重復(fù)步驟(1)(2)，直到剩余的測(cè)試矢量全部可解。

劃分子集的多少，即為配置通道的個(gè)數(shù)，而劃分子集的長(zhǎng)度(子集中包含測(cè)試矢量的個(gè)數(shù))就是每個(gè)配置向量的作用時(shí)鐘數(shù)。

1.3 反饋配置向量的優(yōu)化

根據(jù)定理(2)可知，非齊次方程可能存在多組解，而解結(jié)構(gòu)的不同，整個(gè)結(jié)構(gòu)的硬件開(kāi)銷也隨之不同，因此為了獲得較少的硬件開(kāi)銷，必須對(duì)方程的通解進(jìn)行尋優(yōu)。

對(duì)于反饋配置向量 CNi=(a1i，a2i，…，ari，Ci)，其中各個(gè)元素取值為0或1，向量中的“1”元素對(duì)應(yīng)著配置網(wǎng)絡(luò)中的門結(jié)構(gòu)，因此要使門結(jié)構(gòu)最少，應(yīng)以尋找通解中“1”最少的一組解向量作為限制條件，同時(shí)因非門比異或門的硬件開(kāi)銷要小，所以還可以在含“1”最少的通解中，盡量選擇Ci=1的解，作為該位最優(yōu)配置解進(jìn)行解空間內(nèi)的尋優(yōu)，尋優(yōu)步驟為:

(1)求出矩陣方程的基解(ξ1，ξ2，…，ξN)和特解η。

(2)將基解矩陣(ξ1，ξ2，…，ξN)T做初等行變換，使每行第一個(gè)非0元素以下和以上的各行對(duì)應(yīng)元素為 0，得(ξ'1，ξ'2，…，ξ'N)T。

(3)計(jì)算 η 中含“1”的個(gè)數(shù)，記I(η)，并在 ξ1'，ξ2'，…，ξN'中找出與 η 重復(fù)度最大的基 ξ'r1，做運(yùn)算η1= η⊕ξ'r1。

(4)計(jì)算I(η1)，并比較I(η)和I(η1)。若I(η)＜I(η1)，則 η 即為最優(yōu)通解，算法停止;若I(η)≥I(η1)，則在余下的 ξ'1，ξ'2，…，ξ'r1-1，ξ'r1+1，…，ξ'N中找出與 η1重復(fù)度最大的基 ξ'r2，重復(fù)(3)(4)兩個(gè)步驟。

(5)在已尋得的所有最優(yōu)通解中，盡量選擇末位為“1”的通解。

2 低功耗測(cè)試生成的設(shè)計(jì)

2.1 測(cè)試功耗的產(chǎn)生與衡量標(biāo)準(zhǔn)

在集成電路測(cè)試過(guò)程中，往往因測(cè)試矢量的相關(guān)性較低，電路節(jié)點(diǎn)的翻轉(zhuǎn)密度高，使得測(cè)試功耗要比正常工作時(shí)的功耗高出數(shù)倍［5-6］，巨大的功耗聚集的熱量不僅會(huì)縮短器件壽命甚至燒毀器件，而且還會(huì)嚴(yán)重影響測(cè)試質(zhì)量。CMOS電路中的功耗來(lái)源主要分為靜態(tài)功耗和動(dòng)態(tài)功耗兩種，其中的動(dòng)態(tài)功耗約占總功耗的90%，因此減少動(dòng)態(tài)功耗是降低系統(tǒng)功耗的有效途徑。對(duì)于被測(cè)電路，當(dāng)連續(xù)輸入測(cè)試矢量對(duì)TPk=(Vk-1，Vk)時(shí)，定義在該區(qū)間的功耗Evk可表示為式(4):

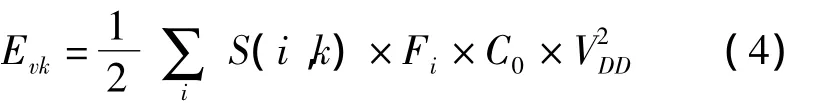
式中i包括電路中所有的節(jié)點(diǎn)，F(xiàn)i為該節(jié)點(diǎn)的扇出數(shù)，C0為單位輸出的負(fù)載電容，VDD代表電源電壓，S(i，k)為矢量對(duì)TPk引起節(jié)點(diǎn)i翻轉(zhuǎn)的次數(shù)，因電源電壓和單位輸出負(fù)載電容是定值，S(i，k)×Fi是功耗分析中唯一可變因素，稱S(i，k)×Fi為TPk作用在節(jié)點(diǎn)i上的WSA(Weighted Switching Activity)，考慮電路總的測(cè)試向量集 TP=(V1，V2，…，Vn)，k=1，2…，n-1。整個(gè)電路總功耗、平均功耗和峰值功耗都可以用WSA進(jìn)行衡量，對(duì)應(yīng)表達(dá)是依次為式(5)～式(7):

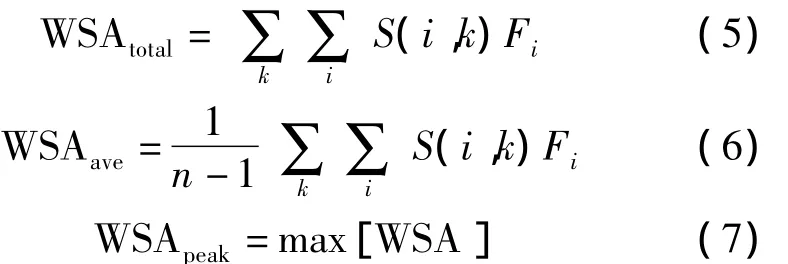
從上面的分析不難發(fā)現(xiàn)，被測(cè)電路的總功耗可以通過(guò)減少測(cè)試集長(zhǎng)度來(lái)降低，也可通過(guò)減少測(cè)試節(jié)點(diǎn)的翻轉(zhuǎn)來(lái)降低;在總功耗一定的情況下，增加測(cè)試集長(zhǎng)度，可以降低平均功耗;電路的峰值功耗只能通過(guò)減少測(cè)試節(jié)點(diǎn)的翻轉(zhuǎn)來(lái)降低。而這里被測(cè)電路內(nèi)部節(jié)點(diǎn)的翻轉(zhuǎn)，正比于其輸入矢量的翻轉(zhuǎn)密度［3］，因此，減少測(cè)試矢量的翻轉(zhuǎn)是降低被測(cè)電路各類功耗的有效方法。

2.2 低功耗測(cè)試結(jié)構(gòu)

為了在不改變已生成的測(cè)試矢量基礎(chǔ)上，得到矢量間單一翻轉(zhuǎn)的測(cè)試矢量，可以采用如圖3所示的LP-TPG(Low Power-Test Patterns Generation)結(jié)構(gòu)［7］，通過(guò)比較原有的相鄰測(cè)試矢量，并用環(huán)形移位寄存器(CSR)按位依次檢測(cè)比較結(jié)果，最后得到單翻轉(zhuǎn)矢量進(jìn)行插入。這樣就保證了總功耗不變的情況下，增加了測(cè)試序列長(zhǎng)度，從而降低平均功耗和峰值功耗。

由于隨著被測(cè)電路輸入端的增多，LP-TPG結(jié)構(gòu)的硬件開(kāi)銷也會(huì)變得很大，因此做如圖4的改進(jìn)，圖中應(yīng)用了可配置LFSR結(jié)構(gòu)替換了傳統(tǒng)的LFSR，并利用了三個(gè)總線選擇器就節(jié)省了原LP-TPG近一半的硬件開(kāi)銷。結(jié)構(gòu)中可配置LFSR分為兩個(gè)部分，即高n/2位(模塊A)和低n/2位(模塊B)(如果被測(cè)電路輸入端為奇數(shù)位，則將最中間的觸發(fā)器同時(shí)并入A、B兩個(gè)模塊)，并將兩部分的現(xiàn)、次態(tài)異或向量分時(shí)段送入n/2位的LP-TPG，原LP-TPG結(jié)構(gòu)中的CSR輸出over信號(hào)，需要經(jīng)歷高n/2位、低n/2位兩次溢出計(jì)數(shù)后(couter=2)，才能輸出over’信號(hào)，并在下一個(gè)clk來(lái)臨時(shí)，使可配置LFSR工作。此外總線選擇信號(hào)也具備以下邏輯:當(dāng)en=1時(shí)，高位進(jìn)入翻轉(zhuǎn)檢測(cè)，低位保留現(xiàn)態(tài)值，即en1=0，en2=0，此時(shí)LP-TPG結(jié)構(gòu)中的couter=1;當(dāng)en=0時(shí)，低位進(jìn)入翻轉(zhuǎn)檢測(cè)，高位保留次態(tài)值，即en1=1，en2=1，此時(shí)couter=2并返回0值。

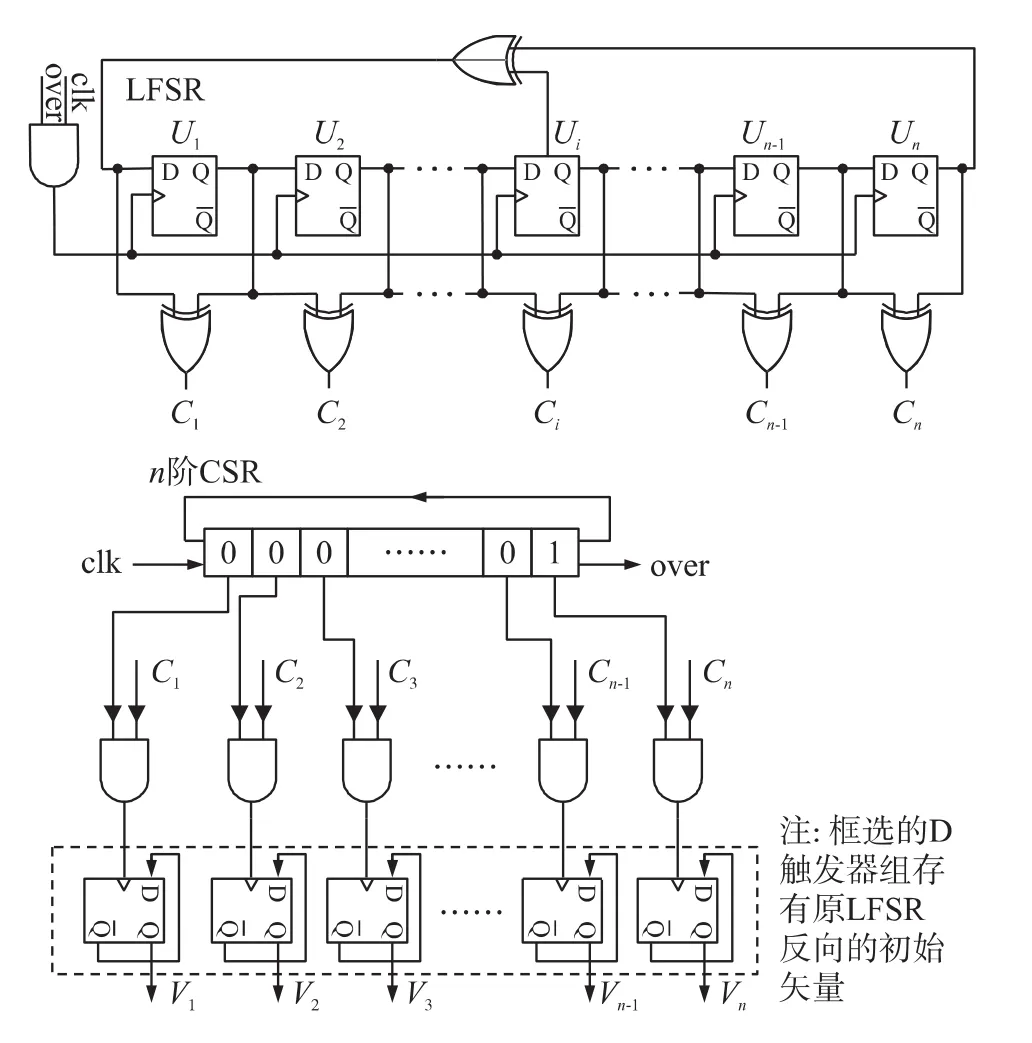
圖3 LP-TPG結(jié)構(gòu)

圖4 基于可配置LFSR的低功耗測(cè)試生成結(jié)構(gòu)

3 實(shí)驗(yàn)及驗(yàn)證

以ISCAS’85實(shí)驗(yàn)中的C17電路為例，利用Atalanta工具對(duì)該電路進(jìn)行故障模擬，在隨機(jī)數(shù)生成器的初始種子為“1358079950”時(shí)，得出的確定性矢量如表1所示，按照式(2)，將全部位的序列代入到式(2)中，得到矩陣方程(8)，并對(duì)該矩陣方程作矢量劃分(式中用虛線標(biāo)出)和通解優(yōu)化處理，最優(yōu)配置結(jié)果如表2所示。

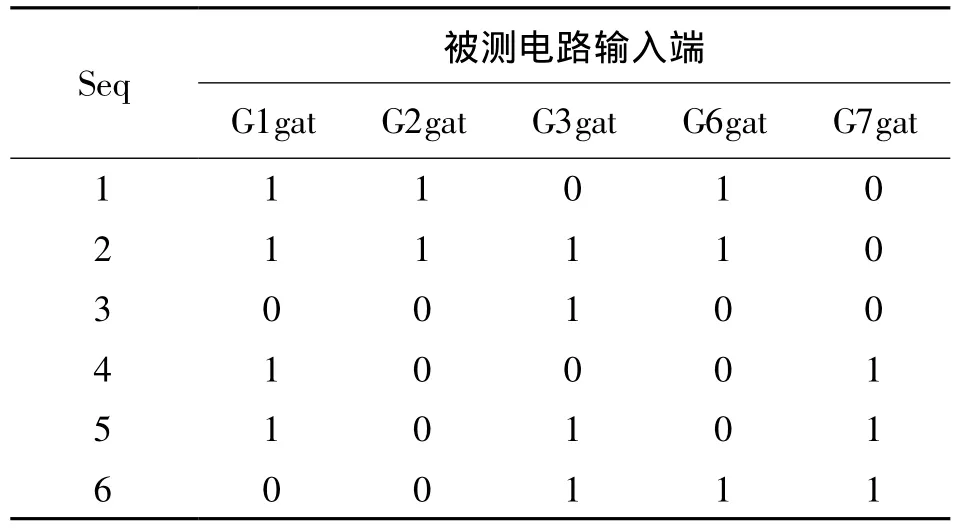
表1 C17電路的確定性矢量

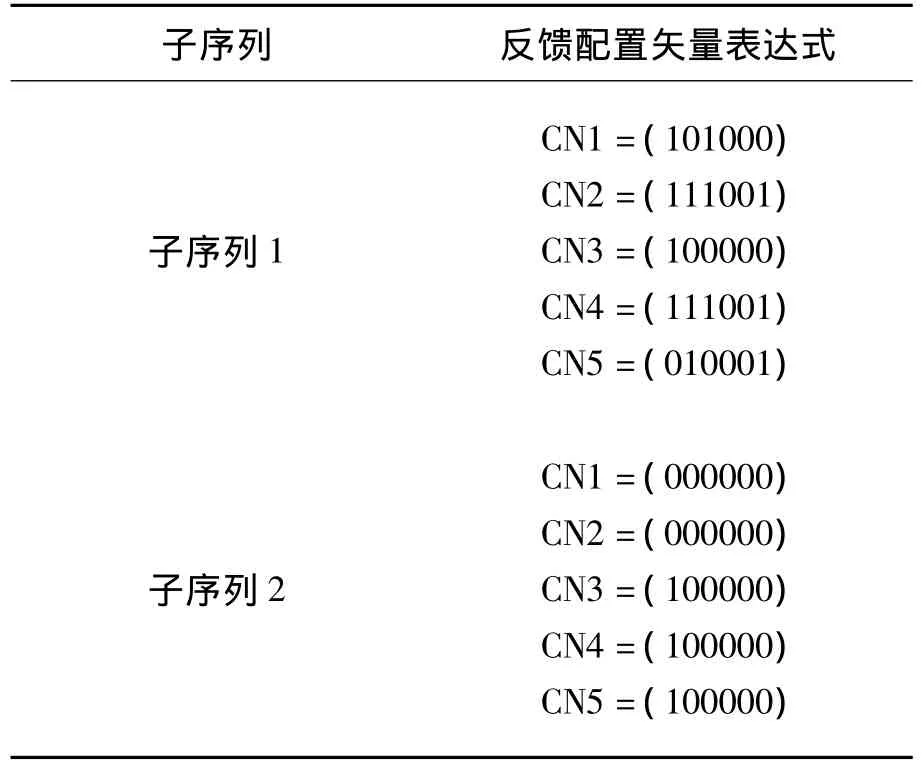
表2 C17電路確定性矢量的優(yōu)化配置

按照矢量劃分原理所得到方程個(gè)數(shù)，加載上述配置至圖4所示結(jié)構(gòu)，并作用相應(yīng)的時(shí)鐘數(shù)，即可在CUT的輸入端得到表3所示的低功耗測(cè)試矢量。

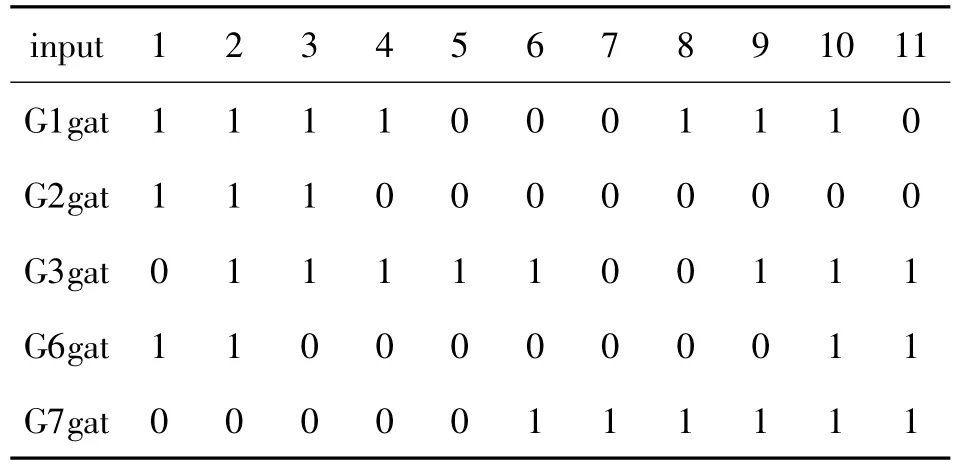
表3 C17電路的低功耗測(cè)試矢量

實(shí)驗(yàn)對(duì)組合電路集ISCAS’85的其他電路也進(jìn)行了確定性矢量的模擬和單一翻轉(zhuǎn)矢量的插入處理，并和文獻(xiàn)［6］進(jìn)行了測(cè)試長(zhǎng)度、電路WSA和故障覆蓋率的比較，如表4所示，實(shí)驗(yàn)中使用了C代碼模擬了DS-LFSR測(cè)試生成過(guò)程和上述結(jié)構(gòu)測(cè)試生成過(guò)程并進(jìn)行WSA的計(jì)算，并應(yīng)用了故障仿真工具fsim進(jìn)行了故障覆蓋率的計(jì)算。

實(shí)驗(yàn)結(jié)果表明，文中提出的低功耗測(cè)試生成方法，總功耗和平均功耗相對(duì)于DS-LFSR方案有大幅度的降低，峰值功耗也有所降低，除此之外，本文方案的測(cè)試集長(zhǎng)度較小，故障覆蓋率也有所提高。

由于本文方案使用的是確定性測(cè)試矢量的生成結(jié)構(gòu)，因此相對(duì)于文獻(xiàn)［6-7］的隨機(jī)性測(cè)試，是在保證故障覆蓋率的前提下，減少了大量隨機(jī)測(cè)試的冗余矢量，同時(shí)插入了單一翻轉(zhuǎn)的測(cè)試矢量，進(jìn)而降低測(cè)試的各類功耗。該結(jié)構(gòu)適合任意組合電路的測(cè)試。不足之處是本文LFSR的配置網(wǎng)絡(luò)相對(duì)于傳統(tǒng)LFSR額外增加了一部分硬件開(kāi)銷。

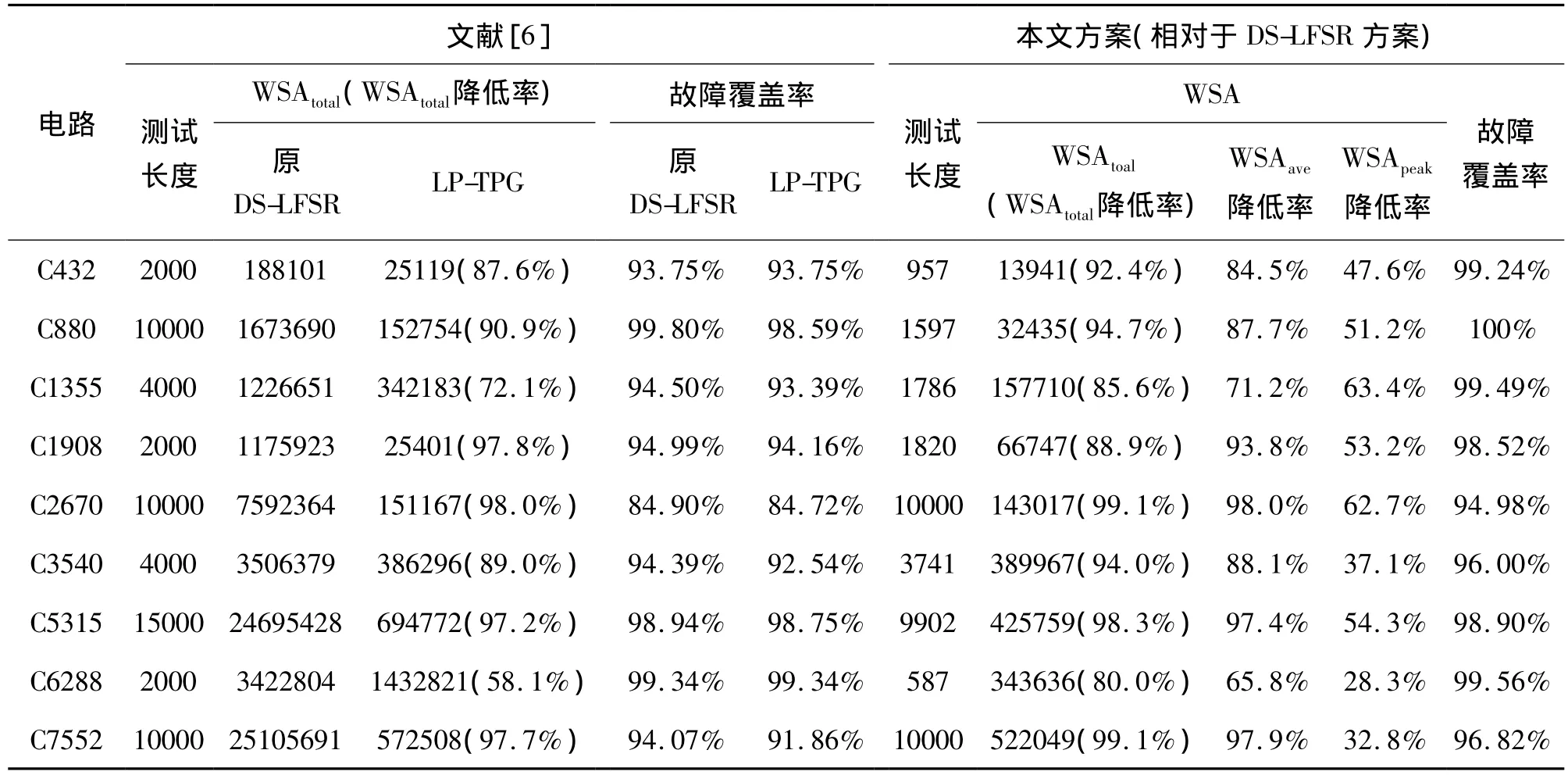
表4 ISCAS’85電路上的實(shí)驗(yàn)結(jié)果

4 結(jié)論

本文提出了一種高故障覆蓋率的低功耗測(cè)試生成結(jié)構(gòu)，結(jié)構(gòu)利用可配置LFSR作為混合測(cè)試矢量生成器，以提高故障覆蓋率，同時(shí)借助已生成矢量的現(xiàn)、次態(tài)異或值，按位逐一插入單跳變矢量，使得系統(tǒng)的各類功耗得到降低。針對(duì)LP-TPG結(jié)構(gòu)，本文利用了異或矢量的分塊處理方法，在不影響原LPTPG工作的前提下，減少了一部分硬件開(kāi)銷。經(jīng)過(guò)對(duì)ISCAS’85電路的實(shí)驗(yàn)，表明了該結(jié)構(gòu)不僅能很大程度上，降低被測(cè)電路總功耗和峰值功耗，而且能夠保證在很高的故障覆蓋率的情況下，減少測(cè)試集長(zhǎng)度以縮短測(cè)試時(shí)間，提高故障檢測(cè)效率，因此對(duì)推動(dòng)低功耗BIST技術(shù)具有一定的意義。

［1］李鑫，梁華國(guó)，陳田，等.基于折疊計(jì)數(shù)器的低功耗確定BIST方案［J］.儀器儀表學(xué)報(bào)，2011，32(12):1-5.

［2］吳義成，梁華國(guó)，李松坤，等.一種基于自選擇狀態(tài)的折疊計(jì)數(shù)器BIST方案［C］//第六屆中國(guó)測(cè)試學(xué)術(shù)會(huì)議論文集，中國(guó)合肥，2010.

［3］Wang S，Gupta S K.DS-LFSR:A BIST TPG for Low Switching Activity［C］//IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2002，21(6):842-851.

［4］談恩民，葉宏，施文康.低功耗BIST設(shè)計(jì)中的加權(quán)DS-LFSR測(cè)試生成方法研究［C］//中國(guó)儀器儀表與測(cè)控技術(shù)交流大會(huì)，中國(guó)四川，2007

［5］Zhang Zhe，Hu Chen，Xiang Wangxue，et al.A Low BIST Methodology Based on Two-Mode LFSR［J］.Chinese Journal of Electron Devices，2004，27(4):705-709.

［6］何蓉暉，李曉維，宮云戰(zhàn).一種低功耗BIST測(cè)試產(chǎn)生器的方案［J］.微電子學(xué)與計(jì)算機(jī)，2003，20(2):36-39.

［7］談恩民，宋勝東，施文康.單/雙跳變向量插入式低功耗BIST設(shè)計(jì)方法［J］.微電子學(xué)與計(jì)算機(jī)，2007，24(7):183-185.

［8］孫海珺，王宣明，盧曉博，等.一種基于格雷碼的電路自測(cè)試序列分配算法［J］.計(jì)算機(jī)學(xué)報(bào)，2011，34(9):1697-1704.

［9］Chen C I H，George K.Configurable Two Dime-Nsional Linear Feed Back Shifter Registers for Parallel and Serial Built-In Self-Test［J］.IEEE Trans，Instrumentation and Measurement，2004，53(4):1005-1014.