LTE上行鏈路中基于探測參考信號的信噪比估計
田 浩 楊 霖 李少謙
(電子科技大學(xué)通信抗干擾技術(shù)國家級重點實驗室 成都 611731)
1 引言
長期演進(jìn)計劃(Long Term Evolution, LTE)系統(tǒng)中,在上行鏈路定義了探測參考信號(Sounding Reference Signal, SRS),用于信道質(zhì)量的探測、頻域調(diào)度及功率控制等操作。SRS覆蓋的范圍通常大于當(dāng)前數(shù)據(jù)的傳輸帶寬,從而可以得到整個信道帶寬內(nèi)的信道質(zhì)量信息,進(jìn)而選擇信道質(zhì)量好的頻帶作為下個時隙數(shù)據(jù)傳輸?shù)男诺李l帶[1]。
衡量信道質(zhì)量的一個重要參數(shù)便是信噪比(Signal-To-Noise Ratio, SNR),目前,研究人員提出的信噪比估計方法主要可以分為兩大類:一類是基于非數(shù)據(jù)輔助的盲估計的方法,如二階矩四階矩方法(M2M4)[2]等。另一類是基于導(dǎo)頻的數(shù)據(jù)輔助的估計方法。由于LTE系統(tǒng)會在頻域發(fā)送一定的導(dǎo)頻來實現(xiàn)系統(tǒng)同步、信道估計等,因此信噪比估計可以利用這些已有的導(dǎo)頻序列來實現(xiàn),不會給通信系統(tǒng)帶來額外的開銷,且精度較高。因此,在LTE系統(tǒng)中多采用的是基于導(dǎo)頻的方法。
在高斯信道(Additive White Gaussian Noise,AWGN)下的信噪比估計方法已經(jīng)發(fā)展得比較成熟了,并且提出了許多經(jīng)典的算法,如最大似然(Maximum Likelihood, ML)算法、最小均方誤差(Minimum Mean Square Error, MMSE)算法[3]等。在無線信道下,由于移動環(huán)境的特殊性,許多經(jīng)典算法不再適用,為此研究人員提出了許多新的算法。例如 Boumard[4]在 2003年提出了應(yīng)用于MIMO-OFDM系統(tǒng)的SNR算法,該方法利用相鄰子載波上的信道系數(shù)的差異來進(jìn)行噪聲估計,但該方法的一大缺點是僅適用于時延擴展較小的信道,當(dāng)信道時延擴展變大時,估計性能將顯著下降;文獻(xiàn)[5]提出了一種迭代的 MMSE算法,但由于需要LMMSE信道估計,復(fù)雜度較高;近年來,Park等人[6]提出了一種 DASS(Difference of Adjacent Subcarrier Signal)算法,該算法通過利用相鄰的 3個子載波上的符號來估計噪聲方差,在低信噪比下性能較好,但是在高信噪比下噪聲估計的誤差較大。上述方法多是基于OFDM系統(tǒng)的,并不完全適用于SRS信號。因此,為了提高SRS信號下的估計性能,本文結(jié)合LTE上行傳輸?shù)奶攸c和SRS的結(jié)構(gòu),提出了一種改進(jìn)的DASS算法。該方法通過重新定義信號頻點的差分方式,提高了高信噪比下的估計性能,并且復(fù)雜度僅為原來方法的1/3。
本文的后續(xù)內(nèi)容安排如下:第2節(jié)介紹SRS傳輸?shù)南到y(tǒng)模型;第3節(jié)對Boumard的方法和DASS方法進(jìn)行描述;第4節(jié)提出一種新的信噪比估計算法;第5節(jié)是仿真驗證;第6節(jié)是結(jié)束語。
2 系統(tǒng)模型
LTE上行鏈路采用的是單載波頻分多址(Single-Carrier Frequency Division Multiple Access,SC-FDMA)的傳輸方式,一個無線幀由10個1 ms的子幀構(gòu)成,每個子幀包含兩個0.5 ms的時隙[7]。在常規(guī)循環(huán)前綴(Cyclic Prefix, CP)配置下,每個時隙由 7 個SC-FDMA 符號組成,在擴展 CP下,每個時隙由6 個SC-FDMA符號組成。當(dāng)一個子幀由高層配置用于發(fā)送SRS時,SRS在該子幀的最后一個SC-FDMA 符號上傳輸[8]。
SRS信號是在 LTE上行發(fā)送的,但是與SC-FDMA數(shù)據(jù)不同的是,對 SRS序列沒有使用DFT擴展,SRS的發(fā)送和接收結(jié)構(gòu)如圖1所示。首先在頻域上生成 SRS序列,然后進(jìn)行物理資源塊(Resource Block, RB)映射,在RB映射之前需要乘以幅度縮放因子βSRS用以與發(fā)送功率PSRS保持一致。SRS采用間隔的方式映射到子載波上,形成“梳狀”的頻域結(jié)構(gòu)[9]。最后,是IFFT變換和加循環(huán)前綴。
假設(shè)已具備良好的同步,并且為簡便起見,本文只考慮單用戶的情形。在接收端,基站根據(jù)頻域起始位置和序列長度將SRS從相應(yīng)的頻域位置提取出來,則接收到的SRS符號上第k個子載波處的數(shù)據(jù)可以表示為

圖1 SRS發(fā)送機和接收機框圖

3 噪聲及信噪比估計
3.1 Boumard的方法

3.2 DASS算法
文獻(xiàn)[6]提出了一種新的 OFDM 系統(tǒng)中估計噪聲的方法,通過使用3個連續(xù)的子載波符號來計算噪聲功率。
系統(tǒng)模型如第2節(jié)所述,為了從接收符號中提取出噪聲成分,定義變量Fk,且有

4 改進(jìn)的DASS算法
DASS算法相比之前的方法能得到較準(zhǔn)確的估計,但是由于該算法最初是應(yīng)用于OFDM系統(tǒng)的,并不完全適應(yīng)SRS的傳輸環(huán)境。這主要是因為在多用戶條件下,SRS采用分布式映射的方式,使得原DASS算法中的假設(shè)條件不再成立。如圖2所示,以兩個用戶為例,UE1的子載波組與UE2的子載波組頻分復(fù)用進(jìn)行傳輸,而這種方式使得某些頻點上的假設(shè)條件 (Hk≈Hk-1≈Hk+1)不再成立,例如,對于處于UE2子載波組兩端的Xn和Xn+1,顯然它們的信道系數(shù)不再近似相等,因此在利用式(6)估計UE1的噪聲時必將引入較大誤差。
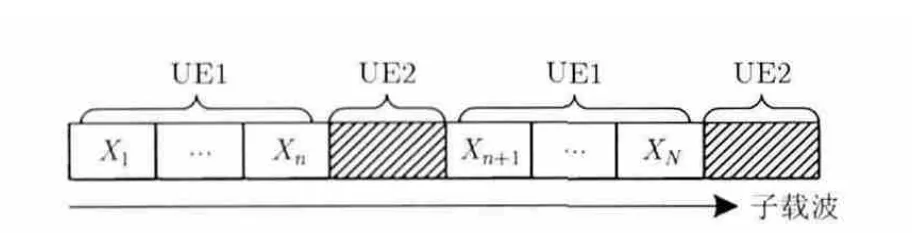
圖2 兩個用戶下SRS的分布式映射方式



圖3 DASS算法的計算示意圖
因此,為了適應(yīng)SRS的傳輸方式以及減少信號能量累積對噪聲估計的影響,本文提出了一種改進(jìn)的DASS算法。如圖4所示,將SRS所占子載波以每3個連續(xù)頻點分為一組,且中間無重復(fù),則總共有為SRS所占的RB數(shù),為整數(shù)),因此組數(shù)為整數(shù)。

圖4 改進(jìn)的DASS算法的計算示意圖
然后,將每組按如下方式分別進(jìn)行計算,重新定義Fk為

其中E(·)代表數(shù)學(xué)期望,2σ為噪聲方差,Im,n為信號與噪聲的交叉項。因此,可得噪聲方差為
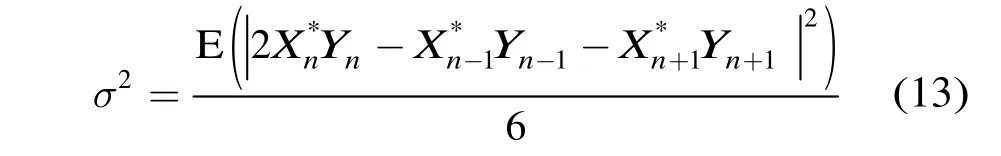
實際系統(tǒng)中,通常用時間平均代替數(shù)學(xué)期望。
5 仿真結(jié)果
下面通過計算機仿真來驗證本文提出的改進(jìn)DASS算法,并與其它算法進(jìn)行了比較。相應(yīng)的系統(tǒng)參數(shù)設(shè)置如表 1所示。

表1 仿真參數(shù)
擴展 ITU模型主要考慮了 EPA5, EVA70和ETU300。這3種模型的多普勒頻移分別為5 Hz, 70 Hz和300 Hz,均方根時延擴展τrms分別為43 ns, 357 ns和991 ns,分別代表低時延、中時延和高時延擴展的信道,具體的多徑時延參數(shù)值可以參考文獻(xiàn)[11]。
為了衡量信噪比估計的性能,下面通過歸一化均方誤差(Normalized Mean Squared Error, NMSE)作為性能的評價指標(biāo),平均信噪比的NMSE定義為
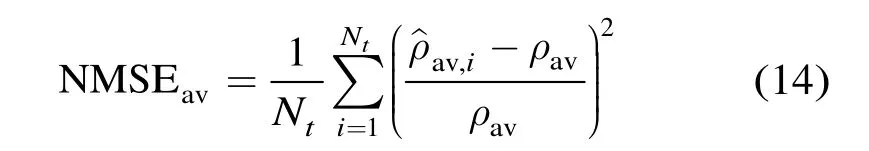
圖 5~圖 7分別給出了 SRS信號在 EPA5,EVA70和ETU300信道模型下的信噪比估計曲線。
從圖5~圖7可以看出,在幾種典型的信道條件下,本文提出的改進(jìn)的DASS算法的性能都優(yōu)于其它方法, 且在高信噪比區(qū)域性能得到了明顯的提升。例如在EVA70信道下,改進(jìn)的方法在信噪比為30 dB的時候比原 DASS算法[6]的性能提升了約 7 dB。而在信道條件最差的ETU300信道下,在高信噪比區(qū)域也比 DASS算法提升了約 3 dB。尤其在EPA5信道下, 改進(jìn)的 DASS算法的信噪比估計曲線基本與實際信噪比曲線相重合。
而Boumard的方法[4]雖然實現(xiàn)簡單,復(fù)雜度低,但缺點是僅適用于時延擴展較小的信道,當(dāng)信道時延擴展變大時,信噪比估計性能將顯著下降。另外從圖中還可以看出,當(dāng)信噪比較高或較低時,Boumard方法的信噪比估計值都將趨于一恒定值,出現(xiàn)所謂的錯誤平層(error floor),嚴(yán)重影響估計的準(zhǔn)確性。原始的DASS算法雖然在低信噪比時能較好地吻合實際的信噪比值,但是隨著信噪比的繼續(xù)攀升,該算法受殘留信號能量的影響越來越大,因此,在高信噪比區(qū)域出現(xiàn)了較大偏差。
圖8~圖10分別為EPA5, EVA70和ETU300信道下的平均SNR估計的NMSE曲線。從圖中可以看出,由于易受信道時延變化的影響,Boumard算法[4]對信道的頻率選擇性十分敏感,其NMSE在SNR大于5 dB的時候快速增加。而原始的DASS算法[6]由于SRS的分布式映射導(dǎo)致某些頻點的信道響應(yīng)相差過大,以及殘留的信號能量對噪聲的影響,使得在高信噪比下噪聲估計偏離真實值。另外,在DASS算法中對首尾兩個符號(F1和FM)只使用了其相鄰的一個子載波(類似Boumard的方法),誤差較大,因此,當(dāng)信噪比增加時DASS算法的錯誤率也迅速增加。

圖5 EPA5信道下的信噪比估計均值曲線

圖6 EVA70信道下的信噪比估計均值曲線
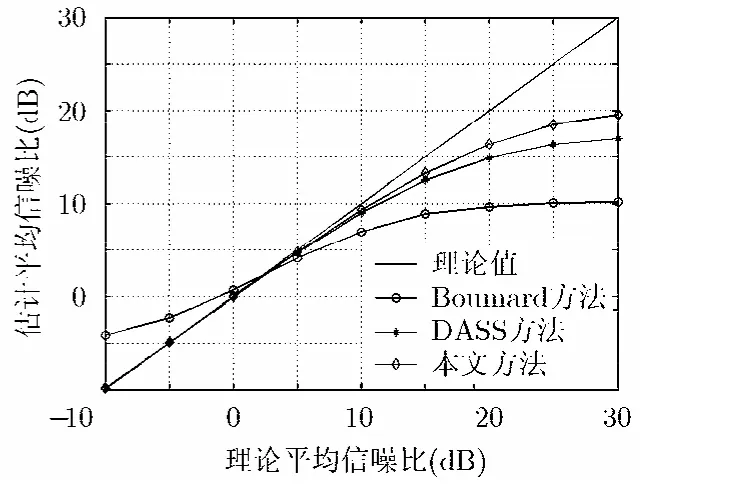
圖7 ETU300信道下的信噪比估計均值曲線
從圖中可以看出,改進(jìn)DASS算法在主要的信噪比區(qū)域性能都較好。例如在EPA5信道下,當(dāng)信噪比大于5 dB的時候NMSE 都維持在 1 0-2左右;在EVA70信道下,在5 dB到20 dB的主要信噪比區(qū)域NMSE 也基本在 1 0-2左右,在高信噪比區(qū)域,其上升趨勢也比較平坦,即使在信噪比為30 dB的時候,NMSE也在 1 0-1左右;由于ETU模型具有5000 ns的最大額外時延擴展,具有強頻率選擇性衰落,因此,該信道下所有算法的性能都出現(xiàn)了明顯下降。實際上這種模型主要用于在不常發(fā)生的超大城市、郊區(qū)和農(nóng)村情形中。但是,即使在最惡劣的信道條件下本文方法的 NMSE值仍小于其余的方法,說明本文提出的方法是有效的。

圖8 EPA5信道下的平均SNR估計的NMSE曲線

圖9 EVA70信道下的平均 SNR估計的NMSE曲線

圖10 ETU300信道下的平 均SNR估計的NMSE曲線
另一方面,改進(jìn)的DASS算法在運算量和復(fù)雜度方面也得到了改進(jìn)。原始的DASS算法在估計噪聲時,對每個SRS信號頻點需要同時利用前后兩個相鄰的信號信息,導(dǎo)致該方法存在重復(fù)計算。由式(7)可知,每個子載波符號都對應(yīng)一個表達(dá)式Fk,因此,該方法總共需要M次(M為 SRS序列長度)差分運算,這當(dāng)SRS序列較長的時候是不利的。而由圖4和式(11)可以看出,改進(jìn)的DASS算法是每3個連續(xù)的SRS頻點計算一次噪聲,且中間不存在重復(fù)利用這些符號,即每3個SRS頻點對應(yīng)一個Fk。因此,本文提出的方法只需要M/3次多項式計算,大大減少了算法的運算量和復(fù)雜度,更易于在實際通信系統(tǒng)中實現(xiàn)。
6 結(jié)束語
本文主要研究了SRS的信噪比估計算法,并針對DASS算法中因信號能量累積導(dǎo)致噪聲估計過大這一缺點,提出了一種改進(jìn)的算法。該方法主要是通過重新定義SRS頻點的分組方式,避免了某些頻點的信道響應(yīng)相差過大,減少了信號能量對噪聲的影響,并且由于對連續(xù)的3個信號頻點,僅需要估計一次噪聲,本方法的復(fù)雜度僅為原DASS方法的1/3。仿真結(jié)果表明,所提方法的估計性能優(yōu)于其余的方法,有效地提高了高信噪比時的估計精度;另一方面,在估計精度一定的情況下,本文提出的信噪比估計方法適用范圍更寬。
[1] 邵道炯. TD-LTE上行鏈路中參考信號技術(shù)的研究與DSP實現(xiàn)[D]. [碩士論文], 電子科技大學(xué), 2011.Shao Dao-jiong. The research and DSP realization of reference signal technology in TD-LTE uplink[D]. [Master dissertation], University of Electronic Science and Technology of China, 2011.
[2] Wang Ai-fen and Xu Hua. Comparison of several SNR estimators for QPSK modulations[C]. 2012 International Conference on Computer Science and Service System,Nanjing , China, Aug. 11-13, 2012: 77-80.
[3] Pauluzzi R and Beaulieu C. A comparison of the SNR estimation techniques for the AWGN channel[J].IEEE Transactions on Communications, 2000, 48(10): 1681-1691.
[4] Boumard S. Novel noise variance and SNR estimation algorithm for wireless MIMO OFDM systems[C]. IEEE Global Telecommunications Conference, San Francisco, USA,Dec. 1-5, 2003: 1330-1334.
[5] Savaux V, Louet Y, Djoko-Kouam M,et al.. An iterative and joint estimation of SNR and frequency selective channel for OFDM systems[C]. 18th European Wireless Conference,Poznan, Poland, April 18-20, 2012: 1-7.
[6] Park Hyeong-sook, Sugrim S, Spasojevic P,et al.. Noise power and SNR estimation based on the preamble in tri-sectored OFDM systems[C]. IEEE Vehicular Technology Conference (VTC Spring), Yokohama, May 15-18, 2011:1-5.
[7] 3GPP TS 36.211 V10.5.0–2012, Technical specification group radio access network; Evolved Universal Terrestrial Radio Access (E-UTRA); Physical channels and modulation(Release 10)[S]. 2012.
[8] Bertrand P. Channel gain estimation from sounding reference signal in LTE[C]. IEEE Vehicular Technology Conference(VTC Spring), Yokohama, May 15-18, 2011: 1-5.
[9] Zhou Bao-long, Jiang Ling-ge, and Zhao Sheng-jie. Sounding reference signal design for TDD LTE-advanced system[C].IEEE Wireless Communications and Networking Conference,Shanghai, China, April 1-4, 2012: 410-415.
[10] 任光亮, 羅美玲, 常義林. OFDM 系統(tǒng)信噪比估計新方法[J].西安電子科技大學(xué)學(xué)報(自然科學(xué)版), 2007, 34(5): 693-696.Ren Guang-liang, Luo Mei-ling, and Chang Yi-lin. Novel SNR estimation algorithm for OFDM systems[J].Journal of Xidian University(Natural Science Edition), 2007, 34(5):693-696.
[11] 3GPP TS 36.104 V10.8.0–2012, Technical specification group radio access network; Evolved Universal Terrestrial Radio Access (E-UTRA); Base Station (BS) radio transmission and reception (Release 10)[S]. 2012.

