一種抗頻偏的衛星幅相調制信號識別算法

廖燦輝 涂世龍 萬 堅

?

一種抗頻偏的衛星幅相調制信號識別算法

廖燦輝*涂世龍 萬 堅

(盲信號處理國家重點實驗室 成都 610041)

該文針對衛星中的常用調制QPSK, 16QAM和新型調制16APSK, 32APSK，提出一種自適應構造幅度分布模板，并通過計算實際信號幅度分布向量與幅度分布模板間的匹配誤差來進行調制識別的算法。該方法不需要知曉載噪比，不需要人為確定閾值，且對頻偏誤差的容忍能力強，適合實際工程應用。仿真表明，在載噪比為9 dB，符號個數為4000時，該算法對4種調制信號的識別率能達到98%以上，證明了其有效性。

衛星通信；調制識別；APSK；幅度分布

1 引言

通信信號調制識別是指在已知信號調制類型集合的前提下，正確判斷并識別當前信號的調制類型，是信號盲處理領域里的一個重要研究課題[1]。隨著通信技術的發展，各種新型調制方式不斷出現，調制識別也需要不斷發展以適應變化的識別要求。

在衛星通信中，由于衛星轉發器的非線性影響，要求采用的調制方式包絡恒定或起伏很小，因而常采用PSK調制，一般為BPSK, QPSK和8PSK。隨著寬帶衛星業務的增多，頻譜資源變得越來越緊張，需要采用更高階調制方式以提高頻帶利用率，如16QAM。但在應用中，16QAM調制存在較多幅度，通過衛星非線性轉發器時功率效率較低，且接近飽和狀態工作時非線性失真影響很大，增加了預失真校正的復雜性。因而，星座呈圓形且圓周個數少的APSK調制被提出并受到關注[2,3]。目前16APSK和32APSK調制已應用在實際衛星通信中。APSK是一種新型調制，一方面目前針對APSK調制識別的研究非常少。另一方面，已有的很多調制識別算法要求在調制識別前先進行載波同步，而這在盲處理條件下是難以滿足的，使得這類算法的實用性受到限制。鑒于此，本文將針對目前衛星中常用的調制類型，主要是PSK(BPSK, QPSK和8PSK), 16QAM, 16APSK和32APSK，研究抗頻偏識別算法。

這4類調制信號星座具有不同的幅度分布特性，而幅度分布特征不受頻偏誤差影響，能夠很好地滿足應用需求，因此本文考慮提取幅度分布特征進行識別。利用幅度分布特征的識別算法中，文獻[4]直接估計幅度分布的波峰數來識別QAM和16APSK，文獻[5]直接用包絡平方方差來識別不同的QAM，這兩種方法利用幅度比較粗糙，性能受噪聲影響較大，需結合其它特征來提高識別率。其它算法，或者需要已知信噪比來確定幅度分布，或者是選定固定的判決閾值。文獻[6]用遺傳算法優化得到瞬時能量的最優劃分向量，據此計算瞬時能量分布向量來識別各階QAM信號，不足之處是需要根據不同載噪比計算不同的劃分向量，且識別前也需要知道準確載噪比；文獻[7]利用不同QAM調制的幅度取值不同，采用減法聚類得到幅度聚類數目，根據聚類數目來判別調制類型，也需事先設定聚類半徑大小；文獻[8]通過計算星座最小環帶方差進行QAM信號識別，采用的是固定的分類閾值；文獻[9]根據不同QAM星座取值幅度不同，需選定劃分閾值后再構造幅度分布模板來進行識別。

受以上方法啟發，本文提出一種自適應構造幅度分布模板，通過計算實際信號幅度分布與幅度分布模板間的匹配誤差來進行識別的算法。該方法不需要知曉載噪比，不需要人為確定閾值，對頻偏誤差的容忍能力強，適合實際工程應用。

2 信號模型

考慮待識別的調制集為{QPSK, 16QAM, 16APSK, 32APSK}。存在頻偏時，BPSK, QPSK和8PSK具有相同的幅度分布，利用幅度分布特征進行識別時會將其歸為一類。考慮到用于BPSK, QPSK和8PSK識別的算法很多，如利用譜線特征[10, 11]，似然特征[12]等，此處不作詳述，僅選擇QPSK作為代表。

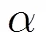
基帶信號波形可表示為

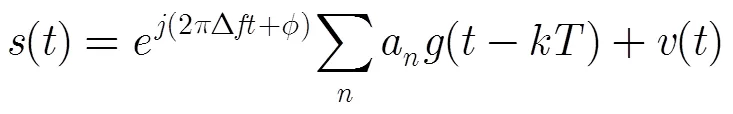
對于QPSK信號，有

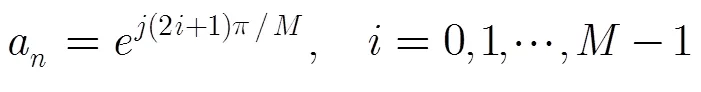
對于16QAM信號，有

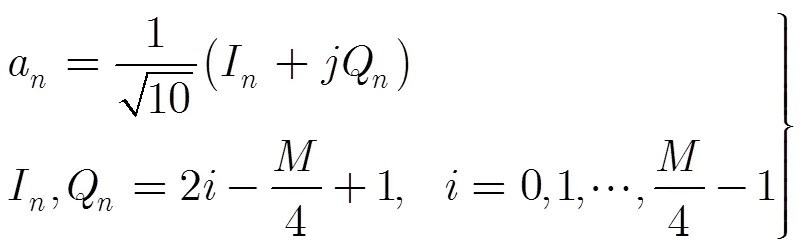
對于APSK信號，有

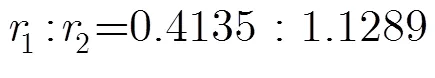
為了消除符號間串擾，可提取信號在最佳采樣位置處的樣點值來進行識別，這些樣點包含了更多調制信息，用于調制識別將會取得更好的效果。本文采用一種非數據輔助的定時估計算法[14]，適用于上面4類調制，具體表達式如式(5)：

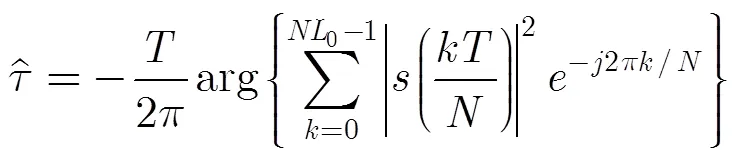
3 識別算法

3.1 星座幅度分布

在存在頻偏情況下，信號星座圖表現為以原點為中心的同心環，星座有幾種幅度，星座圖就表現為幾個同心環。下面對不同調制的這種特性進行分析。

圖1分別給出了QPSK, 16QAM, 16APSK, 32APSK的幅度分布直方圖。QPSK調制星座只有1種幅度，取值概率為1，但是由于噪聲影響，幅度以1為中心呈對稱分布。相應地，16QAM調制星座有3種幅度，16APSK調制星座有2種幅度，32APSK調制星座有3種幅度。不同調制星座幅度分布的中心值及概率見表1。

3.2 模板構造與匹配

根據調制信號星座的不同幅度分布，可以建立不同的幅度分布模板，通過計算實際信號的幅度分布，將其與不同的幅度分布模板比較，計算匹配誤差，選擇匹配誤差最小模板對應的調制為識別出的調制類型。

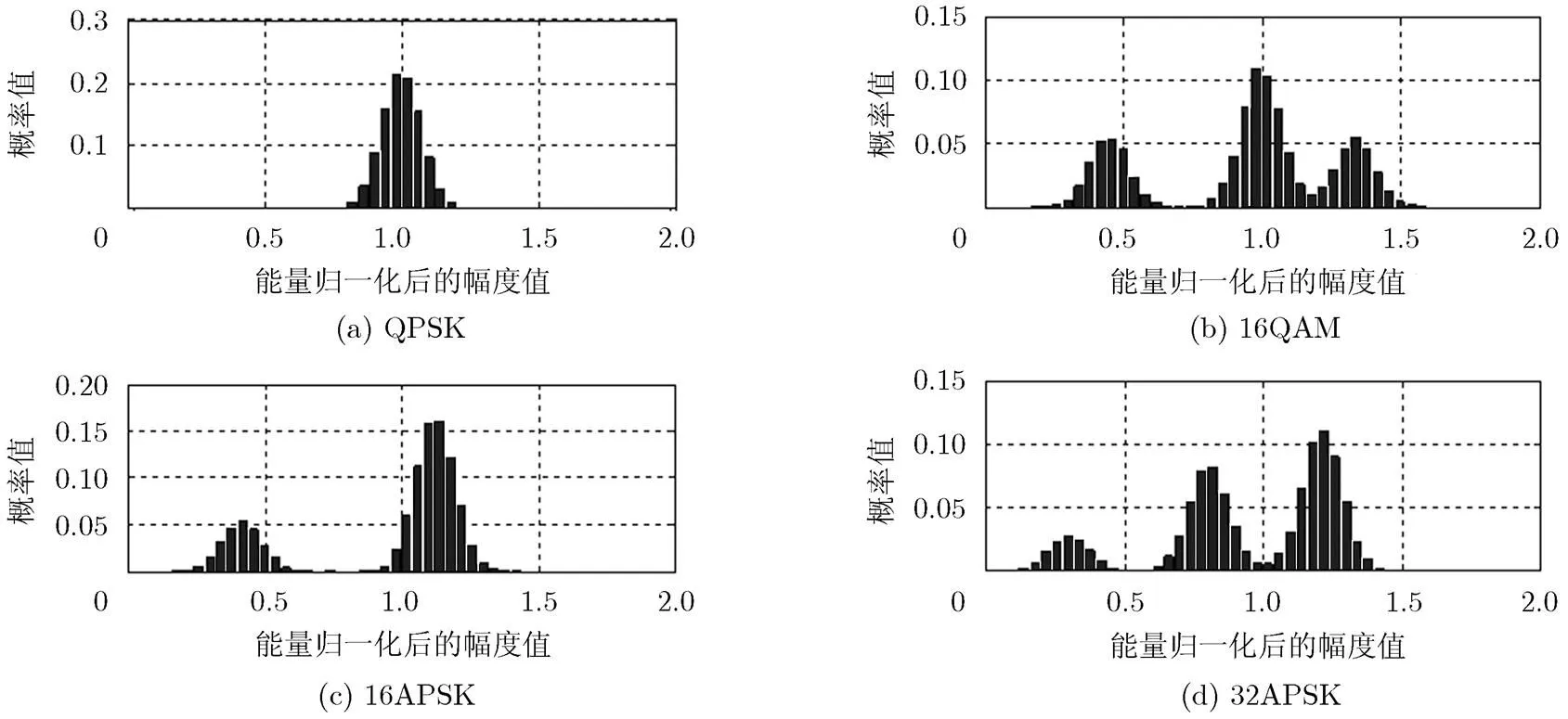
圖1 不同調制星座的幅度直方圖

表1各調制星座幅度分布

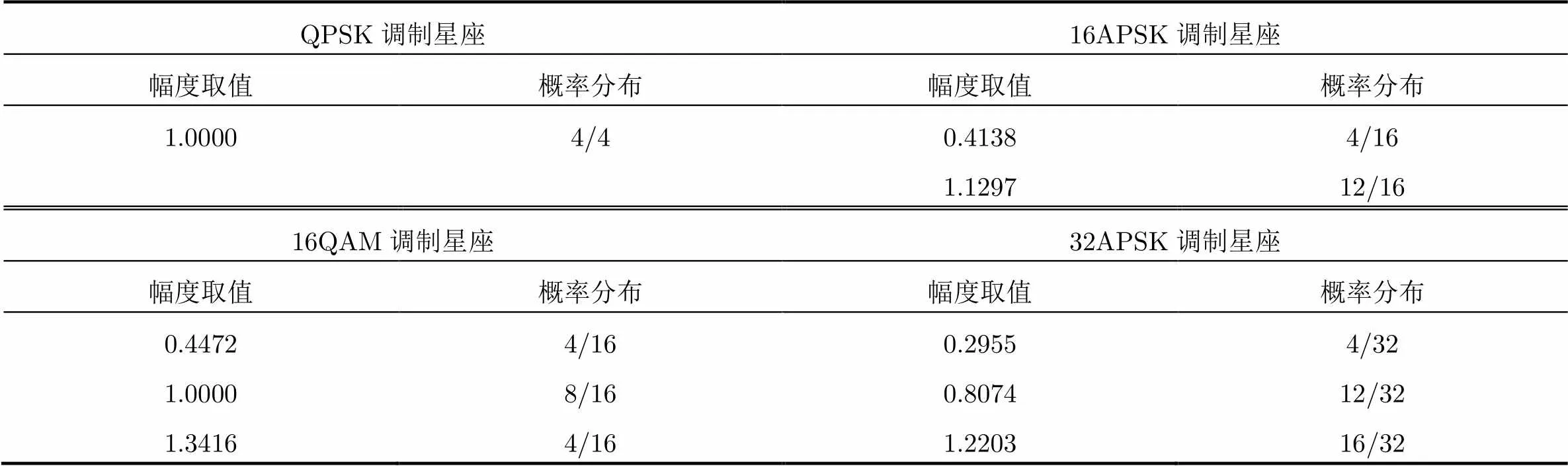
QPSK調制星座16APSK調制星座 幅度取值概率分布幅度取值概率分布 1.00004/40.41384/16 1.129712/16 16QAM調制星座32APSK調制星座 幅度取值概率分布幅度取值概率分布 0.44724/160.29554/32 1.00008/160.807412/32 1.34164/161.220316/32

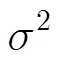
對于其它調制信號，根據相同的原理可構造幅度分布模板。以16APSK為例，調制信號星座有2種幅度取值，則幅度分布模板可設計為

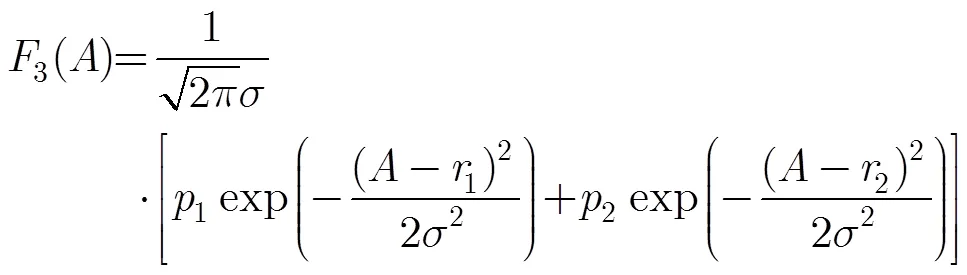
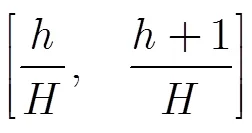
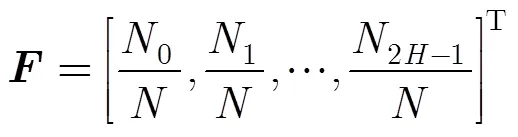
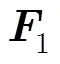
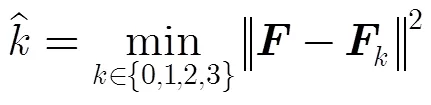
3.3 幅度分布方差估計

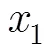
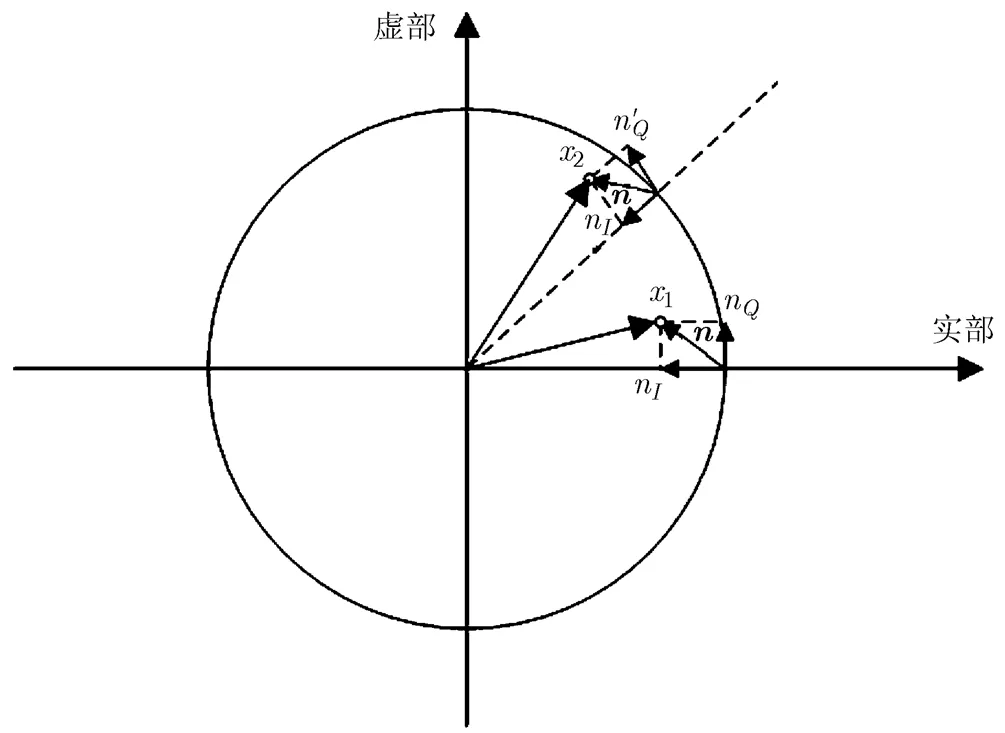
圖2 星座點偏離示意

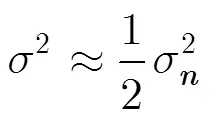
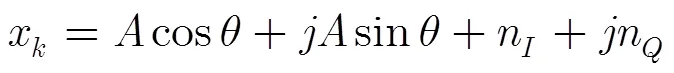
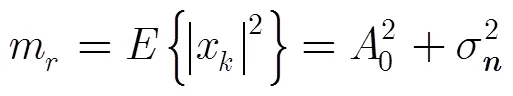
將式(13)代入式(14)中有

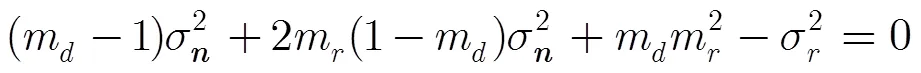
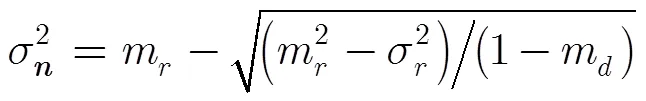
將式(16)代入式(13)，可求得

3.4識別算法流程

根據前面的分析，調制識別算法流程如下：

(1)通過FFT計算出信號頻譜后粗略估計載頻，并通過包絡譜線估計出符號速率，用估計出的載頻進行下變頻，根據符號速率估計值計算均方根升余弦函數進行匹配濾波；

[37] Benjamin K. Wagner, “Lessons from Lassen: Plotting a Proper Course for Freedom of Navigation Operations in the South China Sea”, Journal of East Asia & International Law, Vol. 9, Issue 1 (2016).

(4)對于QPSK, 16QAM, 16APSK和32APSK

4 實驗仿真

4.1 噪聲方差估計性能仿真

第1步 估計信道噪聲方差。圖3給出了能量歸一化下4種調制信號的噪聲方差估計性能曲線，其中實線是根據載噪比值計算出的噪聲方差，虛線是根據實際信號樣本估計出的噪聲方差。可見，4種調制信號的噪聲方差估計值與真實值非常吻合，估計誤差非常小。

第2步 估計幅度分布方差。圖4給出了能量歸一化下4種調制信號的幅度分布方差估計性能曲線，其中實線為根據真實信道噪聲方差用式(11)計算出的近似值，虛線為根據實際信號樣本計算出的估計值。可見，兩者非常接近，表明式(11)的近似是可行的。

綜合圖3，圖4可知，采用文中算法進行幅度分布方差估計是可行的。

4.2幅度分布模板仿真

圖5是根據估計出的幅度分布方差構造出的幅度分布模板，圖6是根據實際星座樣本統計出的幅度分布向量，其中兩個向量均進行了概率歸一化。可見，構造出的幅度分布模板與實際幅度分布向量符合得很好，表明采用模板匹配的思路進行調制識別是可行的。

4.3 調制識別性能仿真

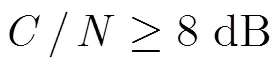
當噪聲增大時，各調制信號星座幅度的環帶分布會變得不明顯，導致出現錯判。由圖7可知，16QAM和32APSK在載噪比較低時識別率較差。在實際應用時，可結合其它特征來克服此不足，如譜線特征。以圖8為例，圖8給出了16QAM調制的誤判性能，可知當載噪比在6~10 dB時，16QAM容易誤判成32APSK。由于16QAM在4倍頻處存在譜線，而32APSK沒有，因此可提取譜線特征來提高16QAM的識別率。需說明的是，實際可結合的其它特征有很多，譜線特征只是其中一種，且在相關文獻中有較多闡述，本文不做詳細敘述，僅作示范說明，讀者在應用時可根據需要結合相關特征使用。

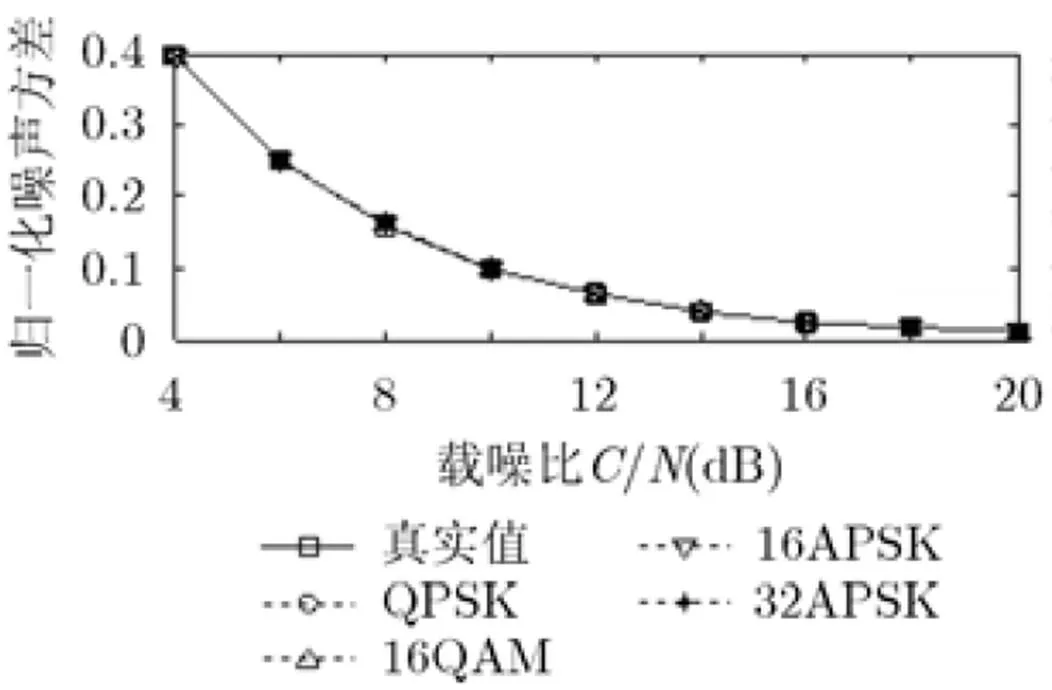
圖3 信道噪聲方差估計性能

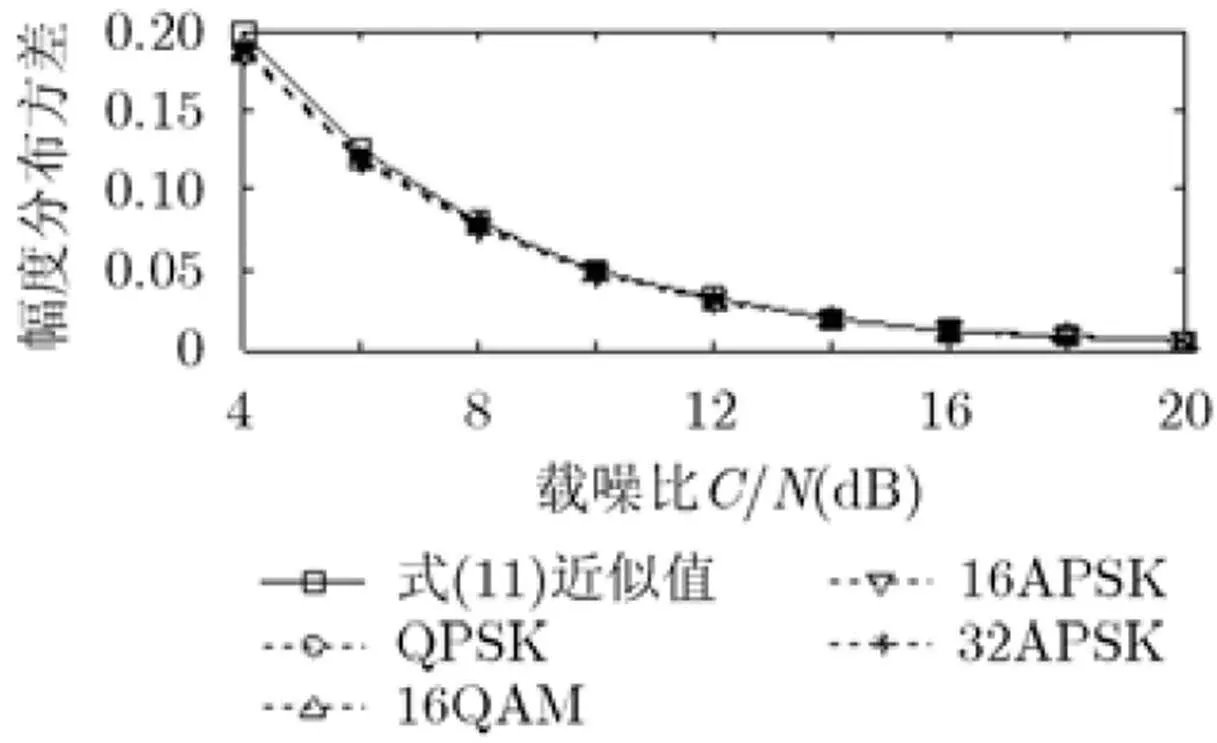
圖4 幅度分布方差估計性能

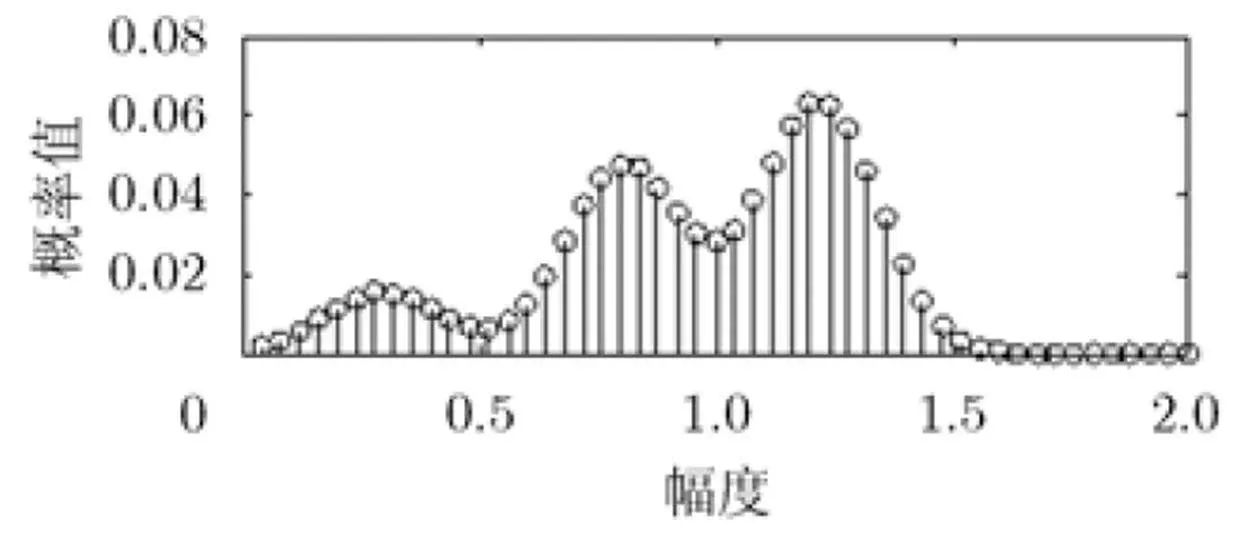
圖5 構造出的幅度分布模板

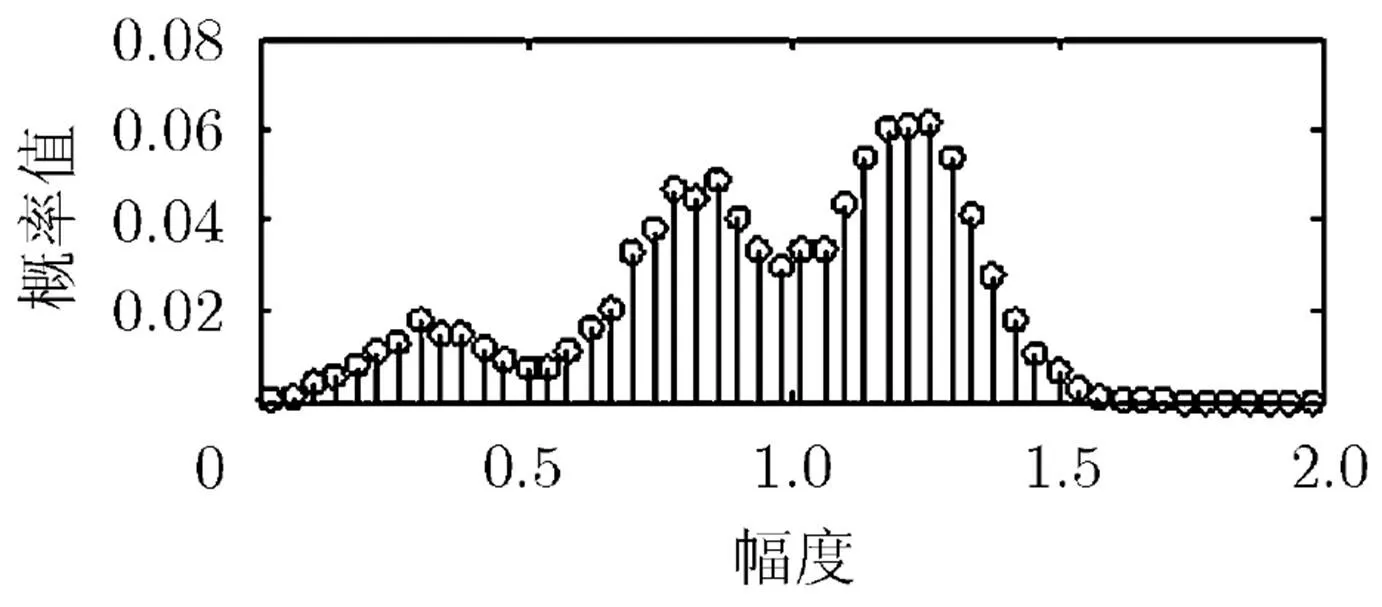
圖6 統計出的幅度分布向量

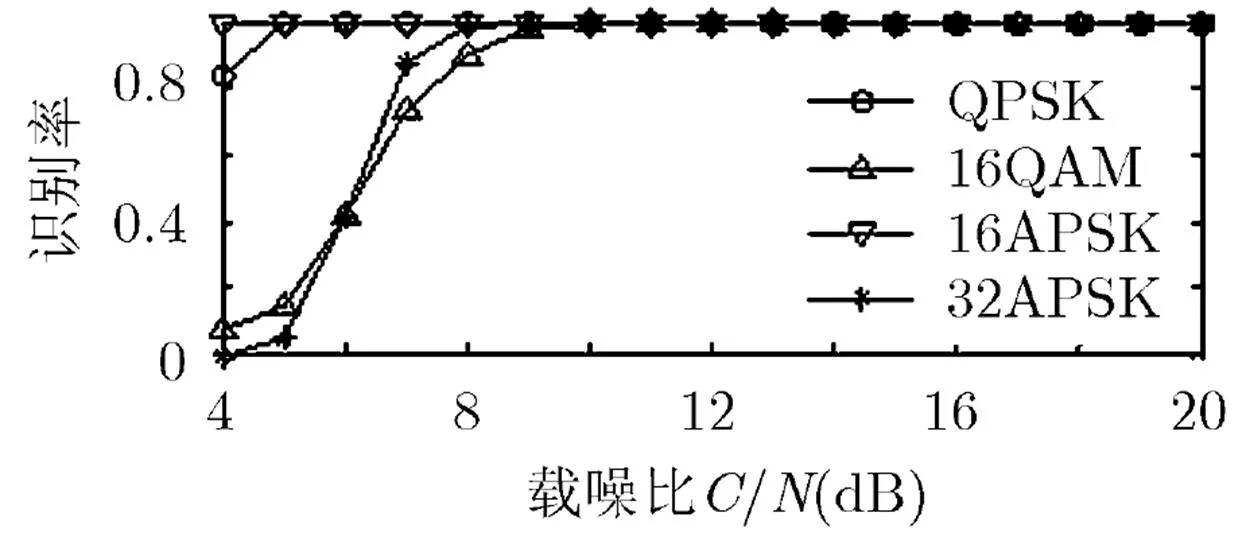
圖7 不同載噪比下的識別性能

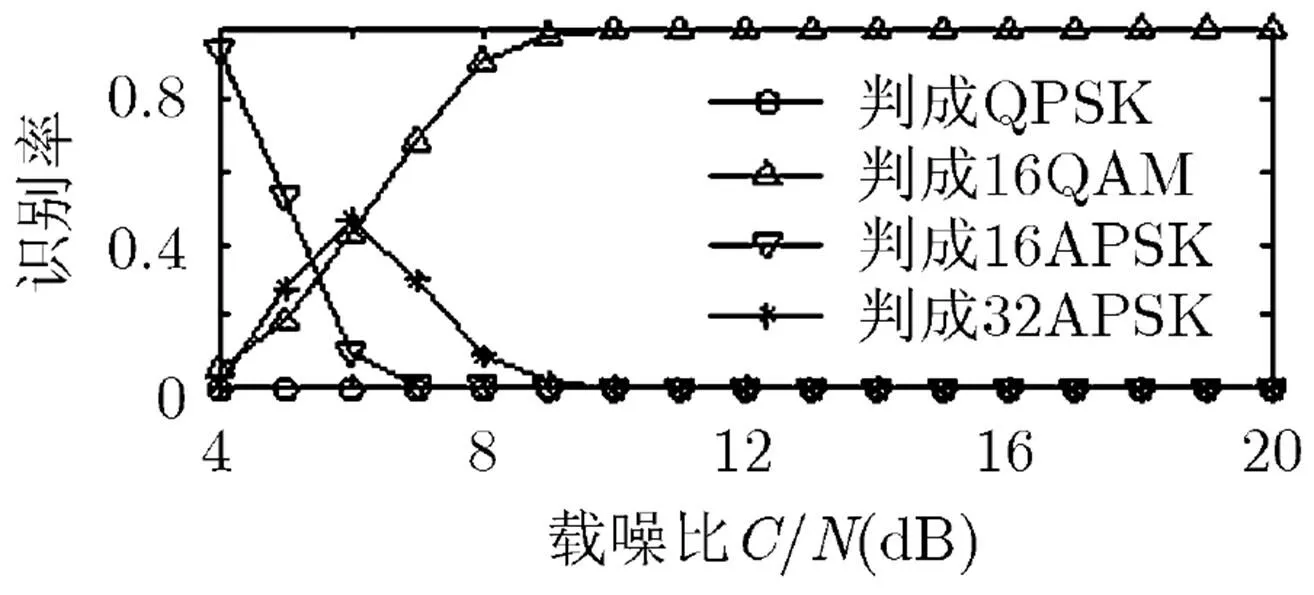
圖8 16QAM調制誤判性能

進一步測試數據長度對識別率的影響。仿真載噪比為10 dB，數據長度從1000個符號開始，每個數據長度進行400次實驗，數據長度步進1000個符號。圖9給出了4種調制信號識別率隨數據長度的變化曲線。當數據長度在2000個符號以上時，QPSK, 16APSK和32APSK的識別率能達到99%以上，16QAM識別率在數據長度達4000個符號以上時，識別率能達到100%。由于實際幅度分布向量是通過統計方式得到的，因此要得到精度較高的幅度分布向量需要較多樣本，一般取數據長度為4000個以上符號時比較合適。

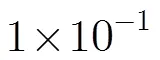
5 結束語

本文主要研究了衛星中常用調制QPSK, 16QAM, 16APSK和32APSK的調制識別問題，提出了一種基于幅度分布向量匹配的調制識別算法。該方法不需要知曉載噪比，不需要人為確定判決閾值，對頻偏誤差的容忍能力強，適合工程應用。值得說明的是，衛星中的調制類型不局限于此4種，除了本文提出的特征，實際可供選擇的特征還有譜線特征、高階累積量特征等。實際識別時一般要結合多類特征來進行，本文只是提供了一類特征的提取思路，并通過仿真證明了其有效性，供讀者在實際應用時參考和選擇。

圖9 不同數據長度下的識別率

圖10 大載頻誤差下的識別性能

[1] Dobre O A, Abdi A, Bar-Ness Y,.. Survey of automatic modulation classification techniques: classical approaches and new trends[J]., 2007, 1(2): 137-156.

[2] 宮曉妍, 劉建偉, 楊友福. 基于衛星信道的APSK調制研究[J]. 遙測遙控, 2009, 30(6): 10-14.

Gong Xiao-yan, Liu Jian-wei, and Yang You-fu. Analysis of APSK modulation based on satellite channel[J]., 2009, 30(6): 10-14.

[3] Xie Qiu-liang, Wang Zhao-cheng, and Yang Zhi-xing. Simplified soft demapper for APSK with product constellation labeling[J]., 2012, 11(7): 2649-2657.

[4] 張宇, 王靈, 陳巖, 等. 衛星通信信號識別技術研究[J]. 航天電子對抗, 2012, 28(5): 27-29.

Zhang Yu, Wang Ling, Chen Yan,.. Satellite communication signal modulation recognition technology[J]., 2012, 28(5): 27-29.

[5] 劉聰杰, 彭華, 吳迪, 等. 突發自適應調制信號的調制識別算法研究[J]. 信號處理, 2012, 28(3): 417-424.

Liu Cong-jie, Peng Hua, Wu Di,.. Modulation recognition algorithm of burst adaptive modulation signal[J]., 2012, 28(3): 417-424.

[6] 褚衍杰, 胡年福, 巢凱今, 等. 通帶MQAM信號調制方式識別方法[J]. 西安電子科技大學學報, 2008, 35(5): 932-937.

Chu Yan-jie, Hu Nian-fu, Chao Kai-jin,Modulation recognition of MQAM signals in the passband[J]., 2008, 35(5): 932-937.

[7] 奚家熹, 王宗欣. 基于Hilbert變換的MQAM信號調制體制識別[J]. 通信學報, 2007, 28(6): 1-6.

Xi Jia-xi and Wang Zong-xin. MQAM modulation scheme recognition using Hilbert transform[J]., 2007, 28(6): 1-6.

[8] 張路平, 王建新. MQAM信號調制方式盲識別[J]. 電子與信息學報, 2011, 33(2): 332-336.

Zhang Lu-ping and Wang Jian-xin. Blind modulation recognition algorithm for MQAM signals[J] .&, 2011, 33(2): 332-336.

[9] 雷德, 許小東, 戴旭初, 等. 大頻偏條件下一種新的調制識別方法[J]. 無線電工程, 2009, 39(4): 25-26.

Lei De, Xu Xiao-dong, Dai Xu-chu,.. A novel modulation recognition scheme under large frequency offset[J]., 2009, 39(4): 25-26.

[10] 楊琳, 許小東, 路友榮, 等. 基于譜線特征的恒包絡數字調制方式識別方法[J]. 中國科學技術大學學報, 2009, 39(9): 936-943.

Yang Lin, Xu Xiao-dong, Lu You-rong,.. Spectrum line based modulation classification for constant modulus digital modulation signals[J] ., 2009, 39(9): 936-943.

[11] 趙嵐. 基于譜線特征的調制方式自動識別方法[J]. 中國電子科學研究院學報, 2012, 7(2): 182-185.

Zhao Lan. Automatic recognition based on spectrum feature for common used modulations[J]., 2012, 7(2): 182-185.

[12] 趙知勁, 朗濤. 基于最大似然比準則的MPSK信號分類方法[J]. 電路與系統學報, 2006, 11(2): 54-57.

Zhao Zhi-jin and Lang Tao. A classification method for MPSK signals based on the maximum likelihood criterion[J]., 2006, 11(2): 54-57.

[13] European Telecommunications Standards Institute. Digital Video Broadcasting (DVB) user guidelines for the second generation system for broadcasting, interactive services, news gathering and other broadband satellite applications (DVB-S2), TR 102 376 v1.1.1 [S]. 2005.

[14] Morelli M, Andrea A N D, and Mengali U. Feedforward ML-based timing estimation with PSK signals[J]., 1997, 1(3): 80-82.

[15] 萬堅, 涂世龍, 廖燦輝, 等. 通信混合信號盲分離理論與技術[M]. 北京: 國防工業出版社, 2012: 127-130.

Wan Jian, Tu Shi-long, Liao Can-hui,.. Theory and Technology on Blind Source Separation of Communication Signals [M]. Beijing: National Defence Industry Press, 2012: 127-130.

廖燦輝： 男，1982年生，博士，工程師，主要研究方向為信號檢測、衛星信號盲處理等.

涂世龍： 男，1980年生，博士，工程師，主要研究方向為信源容錯處理、單通道盲分離等.

萬 堅： 男，1977年生，博士，高級工程師，主要研究方向為衛星通信、盲信號分離等.

An Anti-frequency-offset Algorithm for Modulation Recognition of Satellite Amplitude-phase Modulated Signals

Liao Can-hui Tu Shi-long Wan Jian

(,610041,)

An anti-frequency-offset algorithm is proposed by utilizing amplitude distribution feature for modulation recognition of conventional satellite modulations, such as QPSK, 16QAM and new modulations like 16APSK and 32APSK. The algorithm is based on adaptive construction of amplitude distribution template. After calculating the matching error between the amplitude distribution template and the actual amplitude distribution vector, the algorithm can recognize the modulation type by choosing the modulation type with the minimum matching error. This method does not need any prior knowledge about Carrier-to-Noise ratio (C/N), as well as threshold, and it is not sensitive to frequency offset. Becasuse of these advantages, the algorith is suitable for engineering application. Computer simulations show that the correct recognition probability is more than 98% when C/N is greater than 9 dB and 4000 symbols are used. It verifies the effectiveness of the algorithm.

Satellite communication; Modulation recognition; APSK; Amplitude distribution

TN927

A

1009-5896(2014)02-0346-07

10.3724/SP.J.1146.2013.00512

廖燦輝 liaoch2007@126.com

2013-04-17收到，2013-09-18改回