小時間帶寬積線性調頻信號的脈沖壓縮研究

夏德平，張 良，孟祥東

(南京電子技術研究所， 南京210039)

0 引言

脈沖壓縮技術已廣泛應用到現代雷達系統中，它既能獲得窄脈沖的高距離分辨率，又能保持寬脈沖雷達系統的強檢測能力，同時還是提高雷達抗干擾能力的重要手段。

脈沖壓縮技術通常由大時寬帶寬積(BT)信號經匹配濾波實現［1］，但是經過脈壓輸出并非是理想的單一脈沖，存在著距離旁瓣，在多目標環境下，較強目標回波信號的距離旁瓣可能會淹沒較小目標的回波［2］，進而影響較小目標的檢測。常見的信號波形有線性調頻波形、非線性調頻波形［3］、二相編碼和多相編碼等［4］，其中線性調頻波形應用最早且一直在各種情報雷達中被廣泛應用，也是本文重點研究的對象，但是由于線性調頻信號的最大旁瓣為-13 dB左右，需要采用時域和頻域旁瓣濾波器來抑制距離旁瓣［5-8］，從而不影響較小目標的檢測。

在雷達實際應用中，通常會采用窄帶信號來提高系統抗干擾能力，在這種時寬帶寬積較小的情況下，如采用匹配濾波，或者采用加窗形式都能實現一定的距離旁瓣抑制［9］，但距離旁瓣依然較高，并且信噪比損耗較大，在一定程度上會影響雷達的探測性能。

為了解決該問題，本文通過遺傳算法［10］對這種小時寬帶寬積的線性調頻信號的脈壓性能進行優化，在綜合考慮旁瓣電平、信噪比損失、主瓣寬度等因素基礎上，以脈壓輸出結果作為目標函數，實現了脈壓距離旁瓣的最佳抑制，并且信噪比損失較小，完全滿足雷達系統的探測要求。

1 脈沖壓縮基本原理

1.1 信號模型

假設雷達發射信號為chirp信號，其表達式為

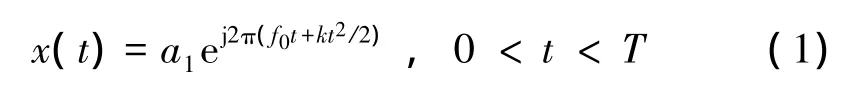
式中:k為調頻頻率(B/T);T為脈沖寬度;B為信號帶寬;f0為載頻。

通過中頻采樣和數字下變頻后，生成I、Q兩路信號，信號如式(2)和式(3)所示，實現如圖1所示。

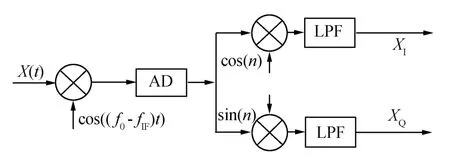
圖1 數字下變頻

I通道信號

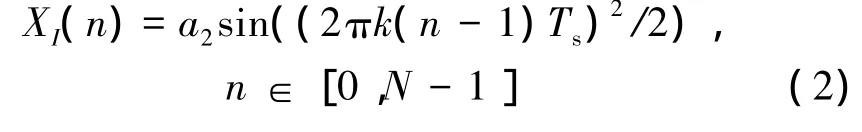
Q通道信號

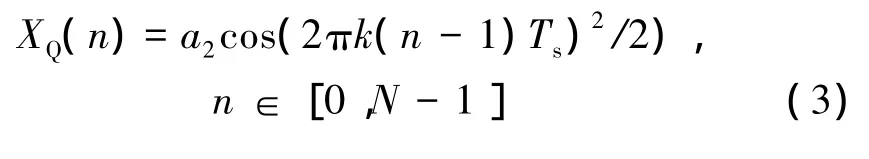
式中:Ts為采樣間隔時間;N為采樣點數。

對上述得到的數字信號，取離散傅里葉變換，變換后的信號如式(4)和式(5)所示。

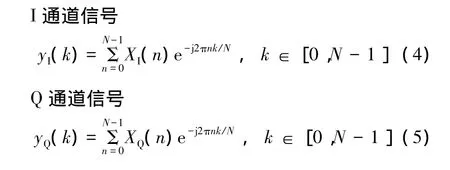
上述式(2)～式(5)得到的信號，可用于進行脈沖壓縮處理。

1.2 脈壓處理原理

通常采用時域脈壓和頻域脈壓兩種手段來實現雷達回波信號的脈沖壓縮。

數字壓縮濾波器可以用非遞歸濾波器的方法實現(即時域脈壓)，雷達回波為 x(n)，n=0，1，…，N-1，匹配濾波器的脈沖響應h(n)為信號x(n)樣本共軛轉置，則脈沖壓縮的輸出為

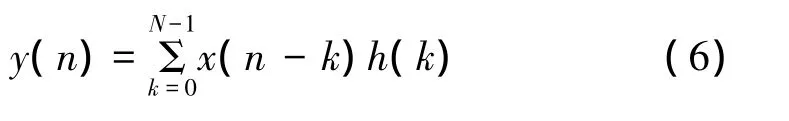
時域脈壓原理框圖如圖2所示，其中*表示卷積，h(n)為匹配系數。

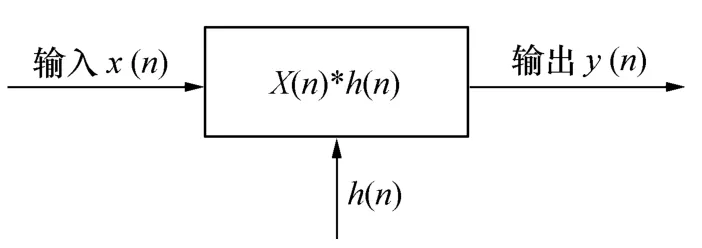
圖2 時域脈壓原理框圖

另一種方法是正反離散傅里葉變換法(即頻域脈壓)，可以采用正反快速傅里葉變換算法來實現離散傅里葉變換和反變換運算，速度要快得多。由于頻域脈壓的高處理效率，所以本方案采用頻域脈壓方法。雷達信號x(t)的頻譜為x(k)，那么，匹配濾波器的傳遞函數為h(t)=xH(t)，其頻譜為h(k)，則脈沖壓縮的輸出為

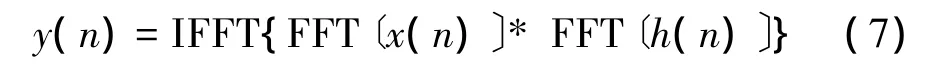
頻域脈壓原理框圖如圖3所示。

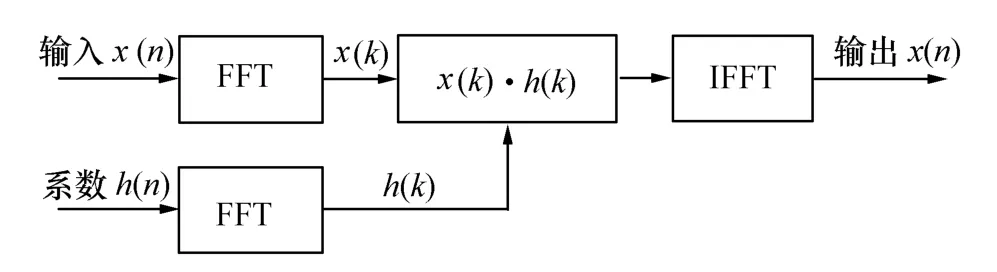
圖3 頻域脈壓原理框圖

為了獲得較低的距離副瓣，線性調頻信號的數字脈沖壓縮可以通過失配濾波(加窗或失配濾波器)的方式獲得。由于不存在所謂“最優”的脈沖壓縮波形或者旁瓣抑制濾波器，波形設計是一個在各個脈壓波形指標之間取折中的過程。一般來講，具有比較好的旁瓣抑制效果的濾波器，信噪比損失則比較大，反之也是一樣。但是，一般的濾波器形式都不具備可以靈活調節的參數(如Hamming窗濾波器、Hanning窗、余弦窗、余弦立方窗、Blackman窗等)或者是雖然有可調節的參數，但是參數本身不具備明確的物理意義(如Taylor窗等)，因此，并不是最佳的濾波器形式。

2 基于相位加權的失配濾波器優化

2.1 遺傳算法優化脈壓系數

本文對用遺傳算法優化失配濾波器的算法開展研究，遺傳算法(GA)是一類借鑒生物界自然選擇和自然遺傳機制的隨機化搜索算法，作為全局優化搜索算法，其具有簡單通用、魯棒性強、適用于并行處理等特點，適合于處理傳統搜索方法難于解決的復雜和非線性問題，目前在眾多領域中均有應用。

用遺傳算法進行優化設計，一般是從一個初始群體出發，依據某一特定的適應度函數評估所有的個體優劣，進行選擇、交叉等遺傳操作，使群體按代數進行，直到滿足給定的精度。

基于遺傳算法進行相位加權的失配濾波器優化設計，選用脈壓輸出的積分旁瓣(Integrated Sidelobe Level，ISL)作為適應度函數，如式(8)所示

式中:y為脈壓輸出;w為脈壓波瓣調控函數，以此作為目標函數。

為優化一個線性調頻信號的脈壓系數，首先，構造初始種群，計算種群中每個個體的適應度，如果滿足需求，則選用，如果不滿足需求，則棄用;其次，以積分旁瓣作為優化目標，同時綜合考慮主瓣寬度、信噪比損失、多普勒敏感性等因素，在同時出現上述幾種因素最優情況時，則可將該脈壓系數作為優選對象。

在考慮主副瓣比約束時，則算法有可能收斂到病態解。為了避免收斂到病態解，被選擇個體在滿足主副瓣比約束條件下，還要滿足一定的主瓣寬度約束條件，即剔除主瓣寬度過寬的編碼。

2.2 fd等因素考慮

在優化脈壓系數的同時要考慮多普勒頻率響應的影響，除了要保證零多普勒速度脈壓旁瓣外，還要保證存在多普勒速度情況下，脈壓旁瓣和信噪比損失性能。

計算多普勒頻率如式(9)所示

式中:v為速度;λ為波長;fd為多普勒頻率。

考慮到多普勒頻率后，信號表示形式如下

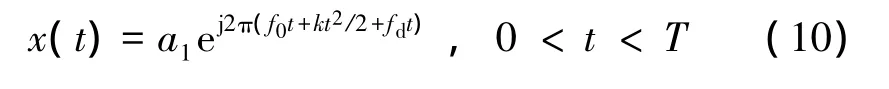
在進行脈壓系數優化時，將目標回波的多普勒頻率帶入優化，可綜合提高性能。但是由于低旁瓣和多普勒性能本身就是相矛盾的，多普勒頻率增大時，脈壓旁瓣必然有一定提高。

3 仿真分析

3.1 仿真條件

仿真條件如下:仿真對象為小時寬帶寬線性調頻信號，信號帶寬為0.4 MHz，脈寬為30 μs，速度范圍為-500 m/s～500 m/s。遺傳算法參數:初始種群為30個，按照適應度函數，選擇65%的個體遺傳到下一代全體中，變異概率為1%。

3.2 線性調頻信號

仿真對象線性調頻信號如圖4所示，左圖為實部和虛部的幅度曲線，右圖為相位調制曲線。

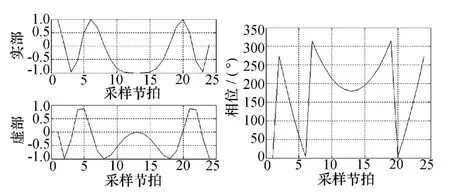
圖4 線性調頻信號

3.3 脈壓結果比對

對該線性調頻信號進行脈壓處理，如直接進行匹配濾波，如圖5a)所示，脈壓最大旁瓣電平為-15 dB;采用加窗處理，加漢明窗，如圖5b)所示，脈壓最大旁瓣電平為-23.9 dB;采用本文的算法優化失配濾波，如圖6所示，脈壓最大旁瓣電平為-38.9 dB。

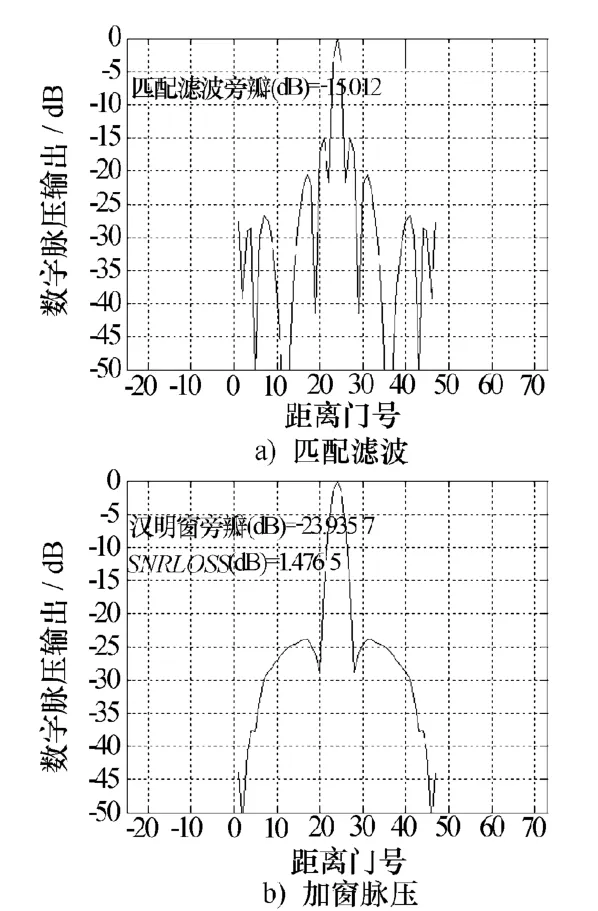
圖5 常規脈壓結果

比較圖5、圖6可以看出，采用遺傳算法優化脈壓系數，與加窗相比，在保持相當的波瓣寬度情況下，最大旁瓣電平優化15 dB，而信噪比損失優化了0.5 dB，并且脈壓旁瓣的平坦度更具有優勢，在大信噪比的情況下，更不易產生虛警。

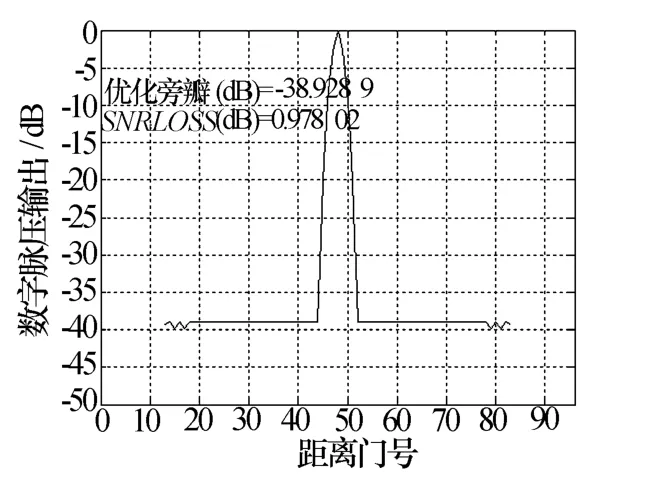
圖6 失配優化脈壓結果

將該算法優化的脈壓系數應用于雷達實際系統，與仿真的結果保持一致，說明該研究結果是有效可行的。如果繼續降低信號的時寬帶寬積，該算法仍有效。但在實際應用中，由于受采樣門的限制，不可能無限制降低信號的時寬帶寬積。所以，在具體應用時，應與雷達的實際系統相結合。

對脈壓系數的多普勒敏感性進行分析，多普勒速度為-500 m/s～500 m/s信號的脈壓結果如圖7所示，從圖中可看出，與零速度相比，±500 m/s處旁瓣電平抬高4 dB，信噪比損失增加0.016 dB，完全可以滿足使用需求。

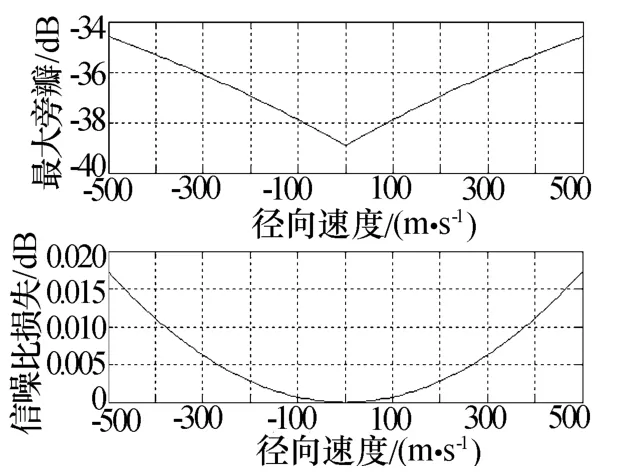
圖7 脈壓性能隨fd變化結果

4 結束語

本文首先對線性調頻信號及匹配濾波器進行分析，在得出采用加窗等算法無法滿足要求的基礎上，提出了利用遺傳算法優化脈壓系數的方法，該算法可以根據設定的目標函數，最大可能地優化脈壓性能，取得實際使用的最優解。理論分析及仿真結果表明，該算法具有設計靈活、副瓣低和保持了線性調頻的多普勒不變性等特點。利用該算法優化的脈壓系數已在雷達系統上得到應用，并取得較好的推廣應用價值。

［1］ 林茂庸，柯有安.雷達信號理論［M］.北京:國防工業出版社，1984.Lin Maoyong，Ke Youan.Theory of radar signal processing［M］.Beijing:National Defense Industry Press，1984.

［2］ Richards M A.雷達信號處理基礎［M］.北京:電子工業出版社，2008.Richards M A.Fundamentals of radar signal processing［M］.Beijing:Publishing House of Electronics Industy，2008.

［3］ Johnston J A ，Fairhead A C.Waveform design and Doppler sensitivity analysis for nonlinear FM chirp pulses［J］.IEE Proceedings，1986，133F(2):163-175.

［4］ Felhaier T.Design and analysis of new P(n，k)polyphase pulse compression codes［J］.IEEE Transactions on Aerospace and Electronic Systems，1994，30(3):865-874.

［5］ Akroyd M H，Ghani F.Optimum mismatched filters for sidelobe suppression［J］.IEEE Transactions on Aerospace and Electronic Systems，1973，9(3):214-218.

［6］ Beden J M，Cohen M N.Optimal sidelobe suppression for biphase codes［C］//1991 National Telesystems Conference.Atlanta GA:IEEE Press，1991:127-131.

［7］ 楊 斌，向敬成，劉 昇.一種數字脈壓旁瓣抑制濾波器設計方法［J］.電子科學學刊，2000，22(1):124-129.Yang Bin，Xiang Jingcheng，Liu Sheng.A method of design digital pulse compression filters for sidelobe suppression［J］.Journal of Electronics，2000，22(1):124-129.

［8］ 王志廣，何 強，韓壯志，等.長M碼序列的失配濾波器設計及其性能分析［J］.現代雷達，2013，35(6):46-49.Wang Zhiguang，He Qiang，Han Zhuangzhi，et al.Design of the mismatch-filter for long M sequences and its performance analysis［J］.Modern Radar，2013，35(6):46-49.

［9］ 蔡風麗，劉新永，江 力.直接加窗加權旁瓣抑制技術研究［J］.安徽電子信息職業技術學院學報，2008，7(5):26-28.Cai Fengli，Liu Xinyong，Jiang Li.Windowing weighted sidelobe suppression technology［J］.Journal of Anhui Vocatioanl College of Electronics ＆ Information Technology，2008，7(5):26-28.

［10］ 陳國良，王煦法，莊鎮泉，等.遺傳算法及其應用［M］.北京:人民郵電出版社，1996.Chen Guoliang，Wang Xufa，Zhuang Zhenquan，et al.Genetic algorithm and applications［M］.Beijing:Posts ＆Telecom Press，1996.