一種多維尺度分析到達時間差定位算法
王 琳,蔣武揚,徐昌慶
(上海交通大學 上海市北斗導航與位置服務重點實驗室,上海 200240)
1 引言
定位技術已經廣泛應用于各個領域,例如通信、礦業、公路、鐵路等等[1-5]。在無線信號廣泛覆蓋的今天,無線定位技術得到了越來越多的重視[6]。在眾多無線定位系統中,到達時間差定位(time difference of arrival,TDOA)是一種被廣泛應用的定位方法。它的原理是通過測量目標點與多個已知參考點之間無線信號傳輸的時間差,得到多組雙曲線方程并求出位置信息。與到達時間定位(time of-arrival,TOA)相比,TDOA技術不需要所有節點的時間同步,也不需要信號帶有時間戳,實現較為簡便。經過學者們的多年研究,TDOA算法得到了不斷的更新和完善。文獻[7]提出的早期算法是一種簡單方便的算法,但其在參考點較多時無法使用。較為經典的泰勒(Taylor)級數展開法精度高、穩定性好,但是需要估計初始位置和遞歸求解,計算量較大[8]。文獻[9]提出的算法即二步加權最小二乘法是另一種經典算法,該算法不需要估計初值并且計算量較小,但是在噪聲較大時性能會明顯變差。
近年來,一種新型的基于多維尺度分析(multi-dimensional scaling,MDS)的TDOA定位算法(以下簡稱MDS算法)[10]引起了研究人員的關注。該方法基于多維尺度分析將TDOA定位問題建模為矩陣范數的最優化問題,然后通過子空間分析將最優化問題轉化為線性方程的求解。該算法定位精度高,計算量較小,并且在噪聲較大時表現良好。
本文指出MDS方法[10]的一處疏漏,即不能通過標量積矩陣的正定性將最優化問題轉化為線性方程求解問題。本文通過分析位置坐標矩陣的列向量的線性相關性,借助幾何意義,得出無論列向量是否線性相關,都有目標線性方程成立,從而嚴格地證明了原算法的正確性,使得原算法的理論基礎更加堅實。
2 系統模型與MDS算法概述
2.1 系統模型
本文針對參考點和目標點位于二維平面上的情形進行討論。
假設有M個位置已知的參考點分布在一個二維平面上,且要求它們并不在一條直線上。設參考點的坐標為(xm,ym)T,m=1,2,...,M。設目標點的坐標為(x0,y0)T,這里假定目標點不與任何一個參考點的位置重合。則第m個參考點到目標點的距離為:
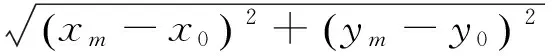
(1)
第m個參考點到目標點的距離與第1個參考點到目標點的距離之差為:
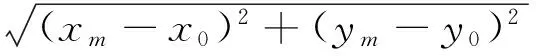
(2)
為方便計,補充定義d1,1=0,d0,1=-d1。
另一方面,dm,1可以通過到達時間差TDOA來測得。設測量所得的目標點發送信號到達第m個參考點的時間與到達第1個參考點的時間的到達時間差(即TDOA)為:τm,1,m=2,3,...,M,則有:
dm,1=cτm,1,m=2,...,M
(3)
其中c表示信號的傳播速度。由式(2)及式(3)可得:
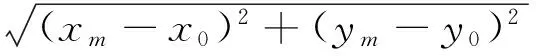
(4)
式(4)是一組非線性方程,其中c是已知量,(xm,ym)T,m=1,2,...,M是已知量,τm,1,m=2,3...M是測量值,(x0,y0)T是待求量,是求解的目標。
2.2 MDS算法概述
MDS算法基于多維尺度分析將TDOA定位問題轉化為矩陣范數的最優化問題,然后通過子空間分析將最優化問題轉化為線性方程的求解問題[10]。以下概述MDS算法的要點。
設wm=(xm,ym,idm,1)T,m=1,2,...,M,設w0=(x0,y0,id0,1)T,其中i是虛數單位。定義位置坐標矩陣為:
(5)
則Z∈M×3是一個包含目標點位置信息x0,y0,d0,1的矩陣。定義標量積矩陣為:
B=ZZT
(6)
則B∈M×M。通過計算可知B的第m行第n列的元素為:
(7)

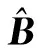
(8)
其中‖·‖F表示矩陣的Frobenius范數。
以下將式(8)的矩陣范數最優化問題轉化為線性方程求解問題。由于B是實對稱矩陣,故可正交相似于對角矩陣。又由于Z為M×3矩陣,而B=ZZT,則r(B)≤r(Z)≤3,其中r(·)表示矩陣的秩。因此B至少有M-3個零特征值,記零特征值對應的特征向量所組成的矩陣為Un,則:
BUn=0
(9)
由式(6)可將式(9)轉化為:
ZZTUn=0
(10)
如果矩陣Z的列向量線性無關,則有:
ZTUn=O
(11)
由于Un是實矩陣,而Z僅有第三列元素是純虛數,其它元素皆為實數,故可將Z的第三列元素的虛數符號i全部去掉,式(11)仍然成立。記為
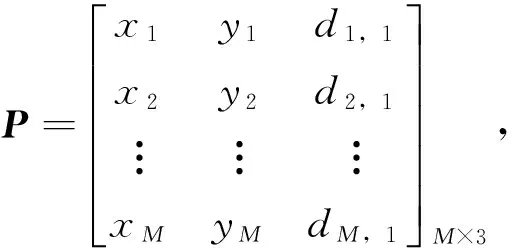
(12)
則可解得:
(13)
式(13)中,v0中的分量x0,y0即是所求的目標點坐標。
3 基于位置坐標矩陣列向量線性相關性的MDS算法
3.1 基于標量積矩陣正定性的MDS算法
文獻[10]中的MDS算法是基于標量積矩陣B的正定性。具體地說,文獻[10]依據標量積矩陣B的正定性來證明式(11)。證明過程如下:
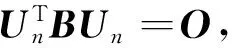
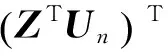
3.2 基于位置坐標矩陣列向量線性相關性的MDS算法
本文給出一種基于位置坐標矩陣列向量線性相關性的MDS算法。該算法總體思路是:當位置坐標矩陣Z的列向量線性無關時,式(11)成立;而當位置坐標矩陣Z的列向量線性相關時,式(11)仍然成立。從而,通過對位置坐標矩陣Z的列向量線性相關性的分析,嚴格地證明了MDS算法的正確性,使得MDS算法的理論基礎更加堅實。
當位置坐標矩陣Z的列向量線性無關時,2.1節已經推導出式(11)成立。
當位置坐標矩陣Z的列向量線性相關時,式(11)成立的理由如下。
如果矩陣Z的列向量線性相關。因為Z是M×3矩陣,那么Z的列秩≤2,因此Z的秩r(Z)≤2,這就等價于Z的行秩≤2,即Z的任意三個行向量都線性相關。由式(5)可見,Z的第三列為純虛數,其它列為實數,為簡便計,可以考慮去掉第三列的虛數符號i,這樣做并不影響行向量的相關性,于是可設:
(14)
注意到:
dm,1-d0,1=(dm-d1)-(-d1)=dm,
m=1,2,...,M
(15)
因此:
(16)

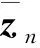
(17)
(xn-x0,yn-y0,dn)=
a1(xk-x0,yk-y0,dk)+
a2(xm-x0,ym-y0,dm)
(18)
考慮式(18)的幾何意義。由于(xk,yk)表示a1,a2中第k個參考點的位置,(x0,y0)為目標點位置,那么容易看出,(xk-x0,yk-y0)中以目標點為起點、以第k個參考點為終點的向量,而dk表示該向量的長度。于是,式(18)可以寫成:
(19)
下面根據a1,a2的正負分類討論:
分類1:假如a1,a2有且僅有一個等于0,不妨設a1=0,a2≠0,則式(19)的第一個方程可以寫為:
(xn-x0,yn-y0)=a2(xm-x0,ym-y0)
(20)
這表示向量(xn-x0,yn-y0)與(xm-x0,ym-y0)共線。同時,由式(19)的第二個方程可知:
dn=a2dm
(21)
由于dn,dm>0,故a2>0。因此(xn-x0,yn-y0)與(xm-x0,ym-y0)共線且同向。
分類2:假設a1,a2均不為0,不妨設a1≤a2,則可以分為以下幾類:
分類2.1:0 (22) 根據向量范數的三角不等式,可知: ‖a1(xk-x0,yk-y0)+a2(xm-x0,ym-y0)‖ (23) 當且僅當向量a1(xk-x0,yk-y0)與a2(xm-x0,ym-y0)共線并且同向時等號成立。又由于0 分類2.2:a1<0 (24) 然后,與分類2.1的原理相同,可知式(24)成立的充要條件是:向量(xn-x0,yn-y0),-a1(xk-x0,yk-y0),a2(xm-x0,ym-y0)共線且同向。由于a1≤a2<0,因此可得向量(xn-x0,yn-y0),(xk-x0,yk-y0),(xm-x0,ym-y0)共線且同向。這與分類2.1得出的結論相同。 分類2.3:a1≤a2<0。由于dl≥0恒成立,因此式(19)的第二個方程無法滿足,因此這種情況下無解。 至此,根據a1,a2的正負分類討論結束。 根據以上的討論,可以得出結論1: 結論1:如果矩陣Z的列向量線性相關,則(xn-x0,yn-y0),(xk-x0,yk-y0),(xm-x0,ym-y0)這三個向量中至少有兩個向量共線且同向。 總結和分析上述結論,可得到結論2: 結論2:如果Z的列向量線性相關,則在M個參考點中任取3個點,目標點都一定落在其中至少兩個參考點所連成的直線上,并且目標點位于該直線上參考點的同側。 假設所有參考點不在一條直線上,因此滿足以上要求的情況只能是: 結論3:如果Z的列向量線性相關,則所有參考點沿著兩條相交的直線排列,而目標點位于這兩條直線交點上;同時,在每條直線上,目標點都位于該直線上所有參考點的同側。 假設參考點和目標點在幾何上滿足結論3所述的排布,則易知矩陣Z的列線性相關。在這種情況下,不妨設第k,m,n個參考點不在結論3所述兩條直線的同一條直線上,那么向量(xn-x0,yn-y0),(xk-x0,yk-y0),(xm-x0,ym-y0)并不兩兩線性相關,因此可知矩陣Z的前兩列的列秩為2。而由于Z的所有三列的列向量線性相關,那么必有Z的第三列可由前兩列線性表示,因此: dm=k1(xm-x0)+k2(ym-y0),m=1,2,...,M (25) 其中,實數k1,k2不同時為0。由式(16)(25)可得: (26) 由式(5)(16)可知: (27) 則式(10)等價于: (28) (29) 其中am∈R是常數。又由式(28)可知: (30) 因此,根據式(29)及式(30)可以得到: (31) 從而: 要使式(32)成立,存在兩種可能的條件: 條件2:k1+k2-1=0。即: k1+k2=1 (33) 為簡便計,不妨假設第1個參考點和第2個參考點與目標點不共線,即向量(x1-x0,y1-y0)與向量(x2-x0,y2-y0)線性無關。根據式(29),有: (34) 利用式(1),則式(33)(34)可以表示為: (35) 其中,xm0=xm-x0,ym0=ym-y0,m=1,2。可設: (36) 將式(35)轉化為: (37) 進一步,可設: k1=cosθ,k2=sinθ (38) 那么,式(37)可以轉化為: (39) 也就是: (40) 這表明θ=α=β。根據α,β的定義式(36),可以得到: (41) 這樣,就得到(x1-x0,y1-y0)與向量(x2-x0,y2-y0)線性相關,與假設矛盾。那么條件2無法成立。 由上述對條件1和條件2的分類討論可知,要使式(32)成立,必須有式(11)成立。 總結全文分析如下:如果矩陣Z的列向量線性無關,則式(11)成立;如果矩陣Z的列向量線性相關,則參考點和目標點在幾何上必須滿足結論3所述的排布,此時必須有式(32)成立,進而式(11)成立。由此可見,無論矩陣Z的列向量是否線性相關,式(11)始終成立。這樣就完成了對文獻[10]疏漏之處的嚴格證明。總之,基于位置坐標矩陣列向量線性相關性的MDS算法克服了基于標量積矩陣正定性的MDS算法[10]的缺陷,在理論上更加嚴格。 本文在概述一種基于MDS的TDOA定位算法基礎上,指出基于標量積矩陣正定性的MDS算法在推導中存在的一處疏漏,即不能通過標量積矩陣B的正定性來得出目標線性方程式(11)。接著,本文提出一種基于位置坐標矩陣列向量線性相關性的MDS算法,該算法從位置坐標矩陣Z的 列向量的線性相關性出發,當Z的列向量線性無關時,式(11)成立;而當Z的列向量線性相關時,通過分析Z的列秩和行秩,得出參考點和目標點所必須滿足的幾何排布條件,并驗證在該條件下仍有式(11)成立,從而嚴格地證明了MDS算法的正確性,使得MDS算法的理論基礎更加堅實。 本文僅針對參考點和目標點位于二維平面上的情形進行討論。對于參考點和目標點位于三維空間中的情形,還有待進一步的研究。 致謝:本項研究工作得到了中國衛星導航系統管理辦公室(北斗辦)和上海市科學技術委員會的聯合資助,資助課題編號為BDZX005. [1] ZEKAVAT R,BUEHRER R M.Handbook of Position Location:Theory,Practice and Advances[M].Hoboken N J:Wiley-IEEE Press,2011. [2] 胡可剛,王樹勛,劉立宏.移動通信中的無線定位技術[J].吉林大學學報:信息科學版,2005,23(4):378-384. [3] 王雪莉,盧才武,顧清華,等.無線定位技術及其在地下礦山中的應用[J].金屬礦山,2009(4):121-125. [4] 胡明偉.無線定位技術應用于實時交通信息采集研究[J].深圳大學學報:理工版,2007,24(3):246-251. [5] 王思詩.高速列車用戶無線網絡定位技術研究[D].北京:北京交通大學,2012. [6] 畢曉偉.無線定位技術研究[D].重慶:重慶大學,2011. [7] FANG B T.Simple Solutions for Hyperbolic and Related Position Fixes[J].IIEEE Transactions on Aerospace and Electronic Systems,1990,26(5):748-753. [8] FOY W H.Position-location Solutions by Taylor-series Estimation [J].IEEE Transactions on Aerospace and Electronic Systems,1976(2):187-194. [9] CHAN Y T,HO K C.A Simple and Efficient Estimator for Hyperbolic Location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915. [10] WEI He-wen,PENG Rong,WAN Qun,et al. Multidimensional Scaling Analysis for Passive Moving Target Localization With TDOA and FDOA Measurements[J].IEEE Transactions on Signal Processing,2010,58(3):1677-1688.
≤‖a1(xk-x0,yk-y0)‖+‖a2(xm-x0,ym-y0)‖
=|a1|‖(xk-x0,yk-y0)‖+|a2|‖(xm-x0,ym-y0)‖
=a1‖(xk-x0,yk-y0)‖+a2‖(xm-x0,ym-y0)‖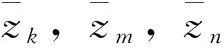


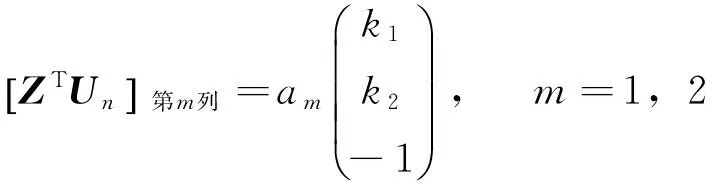
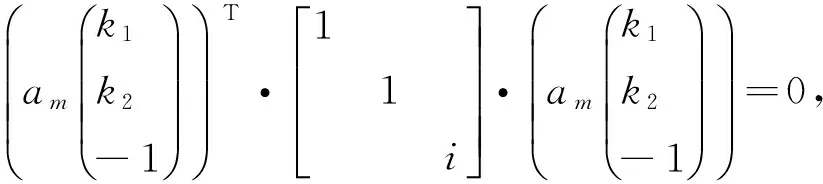

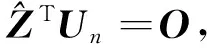


4 結束語

