一種基于有限元分析的楊氏模量的能量等效方法

吳曉東，盛美萍，張安付，屈忠鵬

（西北工業(yè)大學(xué) 航海學(xué)院，陜西 西安 710072）

在研究結(jié)構(gòu)振動(dòng)特性中，楊氏模量一種常用的參數(shù)，用于描述固體材料抵抗形變能力。在結(jié)構(gòu)動(dòng)態(tài)特性研究中，對(duì)于常用金屬材料，可以使用通過靜力試驗(yàn)測(cè)得的楊氏模量值，但對(duì)于粘彈性材料，當(dāng)其受動(dòng)態(tài)力激勵(lì)時(shí)，其楊氏模量是隨激勵(lì)頻率變化的，通常稱為動(dòng)態(tài)楊氏模量，因此，在研究具有粘彈性結(jié)構(gòu)動(dòng)態(tài)特性中就不能使用靜力試驗(yàn)測(cè)得的粘彈性材料靜態(tài)楊氏模量。現(xiàn)已有多種實(shí)驗(yàn)方法[1,2]測(cè)量動(dòng)態(tài)楊氏模量，如正弦力激勵(lì)法、諧振實(shí)驗(yàn)法、自由衰減法、振動(dòng)梁法。動(dòng)態(tài)楊氏模量比靜力法測(cè)得的楊氏模量更真實(shí)地反映結(jié)構(gòu)動(dòng)態(tài)能量特性，但對(duì)結(jié)構(gòu)動(dòng)態(tài)能量特性的軟件仿真和數(shù)值計(jì)算中，輸入動(dòng)態(tài)楊氏模量較為困難或者無法輸入，例如Autosea軟件是計(jì)算結(jié)構(gòu)動(dòng)態(tài)特性的常用軟件，但是只能在Autosea軟件中輸入楊氏模量的常值，這就造成了軟件仿真的誤差。針對(duì)此問題，本文提出了一種運(yùn)用有限元分析，以得到既能反映動(dòng)態(tài)楊氏模量的能量特性，又能便于在軟件中輸入等效楊氏模量，用于該結(jié)構(gòu)的動(dòng)態(tài)特性計(jì)算。該方法以具有粘彈性材料自由阻尼板為例進(jìn)行闡述。此外，由于本文篇幅有限，如無特殊說明，以下楊氏模量簡(jiǎn)稱模量，動(dòng)態(tài)楊氏模量簡(jiǎn)稱動(dòng)態(tài)模量，等效楊氏模量簡(jiǎn)稱等效模量。

1 優(yōu)化可行性分析

波速法可以獲取粘彈性材料自由阻尼板上的阻尼層粘彈性材料的動(dòng)態(tài)楊氏模量。通過波速法獲取4組100~3 000 Hz頻段內(nèi)對(duì)數(shù)平均分布的100個(gè)頻率點(diǎn)處的模量數(shù)據(jù)。其中一組數(shù)據(jù)如圖1所示。

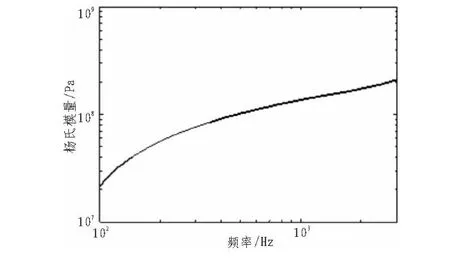
圖1 動(dòng)態(tài)楊氏模量Fig.1 Figure of dynamic Young's modulus

由圖1可知，阻尼材料模量隨頻率增大而增大，低頻增速較快高頻增速放緩，且曲線連續(xù)，與實(shí)際情況相符[1]。結(jié)構(gòu)受激時(shí)，由激勵(lì)點(diǎn)位移ξ和力F求取輸入功率P用以表征激勵(lì)點(diǎn)的能量特性，如式（1）所示[3]

取3個(gè)靜態(tài)模量，分別為模量范圍內(nèi)的下限模量Emin、中間模量Emid和上限模量Emax，分別求取該模量下自由阻尼板結(jié)構(gòu)的輸入功率，并與動(dòng)態(tài)模量下的輸入功率P0比較，如圖2所示。

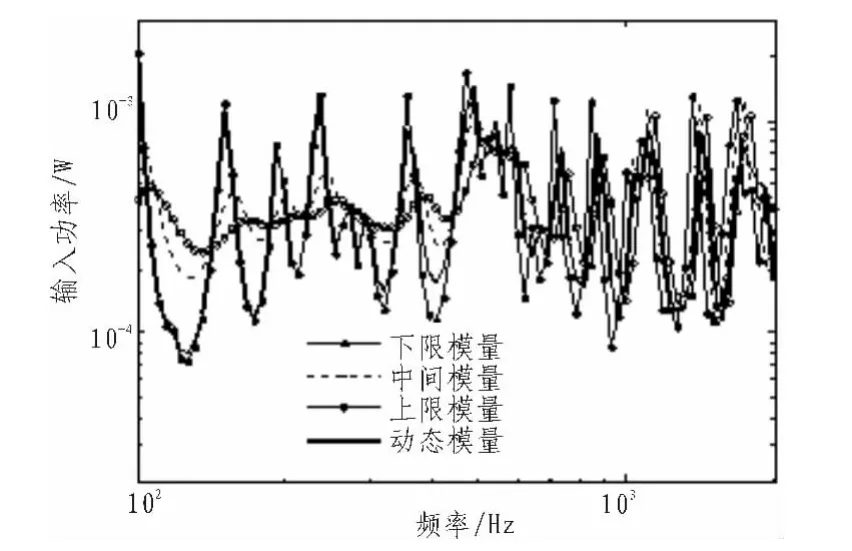
圖2 3種模量常值與動(dòng)態(tài)模量下的輸入功率Fig.2 Input power using dynamic and three constant modulus

由圖2可知，所有輸入功率曲線總體來說較為接近，但各頻段的接近程度不一樣。下限模量的輸入功率在低頻與動(dòng)態(tài)模量輸入功率接近，而上限模量的輸入功率在高頻與動(dòng)態(tài)模量輸入功率接近，這與動(dòng)態(tài)模量隨頻率增大而增大的事實(shí)相符。

任取一模量常值Et，求取該模量下的輸入功率Pt。輸入功率Pt和P0為隨頻率變化的數(shù)組，設(shè)維數(shù)為n，取errort為Pt與P0的誤差的評(píng)估值。

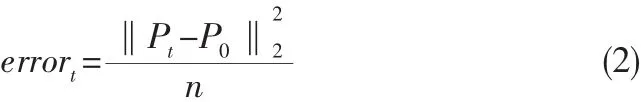
由表1可知，模量常值為1.00×108時(shí)的輸入功率與動(dòng)態(tài)楊氏模量下的輸入功率更為接近，在所選的6組模量常值中，它更能代表動(dòng)態(tài)楊氏模量的能量特征，更反映真實(shí)情況。楊氏模量曲線連續(xù)，則其誤差曲線也連續(xù)，在考察頻率范圍內(nèi)，必存在一個(gè)誤差值最小，最能代表動(dòng)態(tài)模量的模量常值。隨后可用有限元優(yōu)化模塊搜索整個(gè)區(qū)間并獲取最小誤差下的模量常值。

表1 不同模量常值下的輸入功率誤差Tab.1 The error of input power using different constant modulus

2 有限元優(yōu)化

2.1 模型建立

以自由阻尼板為例建立仿真模型，其中基底層長(zhǎng)0.5 m，寬 0.4 m，厚 0.003 m，密度 7 800 kg/m3，泊松比 0.28，楊氏模量 2.06×1011Pa，損耗因子 0.01；阻尼層長(zhǎng) 0.5 m，寬 0.4 m，厚0.01 m，密度1 100 kg/m3，泊松比0.49，其楊氏模量和損耗因子都是隨頻率變化的動(dòng)態(tài)數(shù)據(jù)，逐個(gè)分析頻點(diǎn)賦值。

在ANSYS有限元軟件中建立自由阻尼板的有限元模型。模型基底層采用shell63殼單元，阻尼層采用solid45體單元，自由劃分網(wǎng)格。由于網(wǎng)格尺寸必須小于波長(zhǎng)的1/6，故根據(jù)分析頻率范圍(100~3 000 Hz)和材料參數(shù)，厚0.003 m基底層彎曲波波長(zhǎng)下限為0.420 9 m，0.01 m阻尼層波長(zhǎng)下限為0.131 5 m，故網(wǎng)格尺寸上限分別為0.070 2 m和0.021 9 m[4]。取殼單元尺寸為0.01 m，體單元尺寸為0.003 m，劃分自由網(wǎng)格后，共生成殼單元2 000個(gè)和體單元8 000個(gè)。以板一頂點(diǎn)為原點(diǎn)，以該頂點(diǎn)所在兩邊為X、Y坐標(biāo)，建立平面坐標(biāo)系，激勵(lì)點(diǎn)在坐標(biāo)（0.3,0.3,0）處，激振力為簡(jiǎn)諧激勵(lì)，大小為1 N，按實(shí)驗(yàn)測(cè)量頻點(diǎn)逐個(gè)進(jìn)行諧響應(yīng)分析。激勵(lì)位置如圖3所示，有限元模型如圖4所示。

2.2 分析及數(shù)據(jù)提取

輸入動(dòng)態(tài)模量數(shù)據(jù)和動(dòng)態(tài)損耗因子數(shù)據(jù)，對(duì)圖4結(jié)構(gòu)，按實(shí)驗(yàn)測(cè)量頻點(diǎn)逐個(gè)進(jìn)行諧響應(yīng)分析，提取激勵(lì)點(diǎn)的力和位移數(shù)據(jù)，求得每個(gè)頻率點(diǎn)處的輸入功率，以獲得動(dòng)態(tài)模量輸入功率 P0。

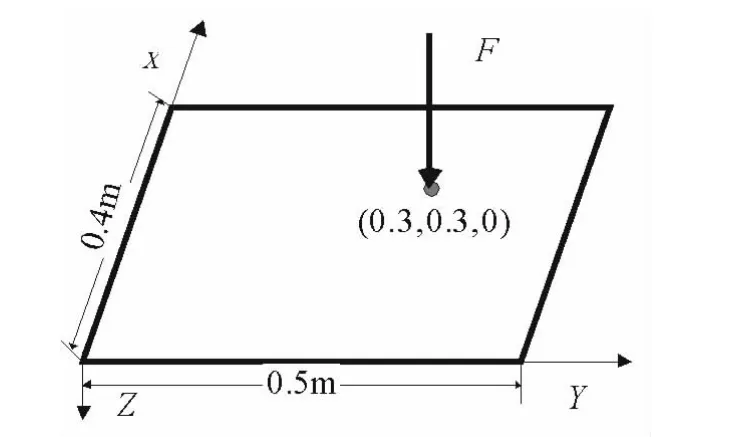
圖3 激勵(lì)位置Fig.3 The point to excite the structure

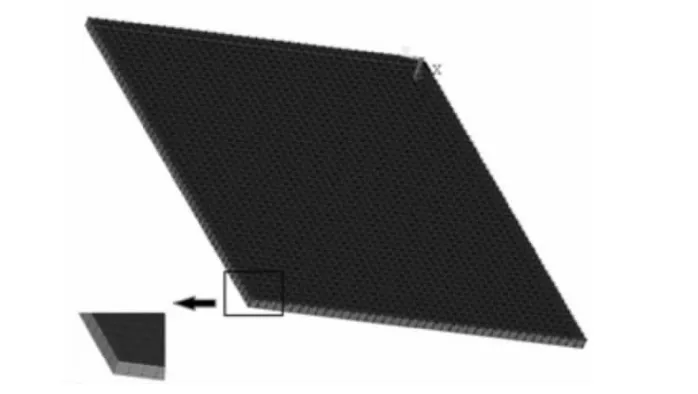
圖4 有限元分析模型Fig.4 The FEA model

2.3 優(yōu)化設(shè)計(jì)

再進(jìn)行預(yù)分析，輸入模量常值和動(dòng)態(tài)損耗因子數(shù)據(jù)，同樣對(duì)圖4結(jié)構(gòu)，按實(shí)驗(yàn)測(cè)量頻點(diǎn)逐個(gè)進(jìn)行諧響應(yīng)分析，提取激勵(lì)點(diǎn)的力和位移數(shù)據(jù)，求得每個(gè)頻率點(diǎn)處的輸入功率，得到模量常值輸入功率Pt，再根據(jù)模量常值輸入功率Pt和動(dòng)態(tài)模量輸入功率P0，獲取二者誤差errort。

以模量常值Et為設(shè)計(jì)變量，以模量常值輸入功率Pt與動(dòng)態(tài)模量輸入功率P0的誤差errort為目標(biāo)變量，調(diào)用ANSYS優(yōu)化模塊進(jìn)行優(yōu)化。ANSYS優(yōu)化模塊中的優(yōu)化算法有零階方法、一階方法、隨機(jī)搜索法、等步長(zhǎng)搜索法、乘子計(jì)算法、最優(yōu)梯度法和用戶自定義方法。

由于優(yōu)化目標(biāo)變量分布情況未知，故本文先用等步長(zhǎng)搜索法確定整個(gè)頻率空間內(nèi)誤差分布，確定局部極小值點(diǎn)范圍，再對(duì)每個(gè)極小值點(diǎn)，縮小設(shè)計(jì)變量取值范圍，縮小收斂界限，進(jìn)行一階分析，精確地找出最小誤差的局部極值點(diǎn)，誤差最小的局部極小值則為優(yōu)化后的優(yōu)化模量值。詳細(xì)優(yōu)化流程及程序代碼如圖5所示。

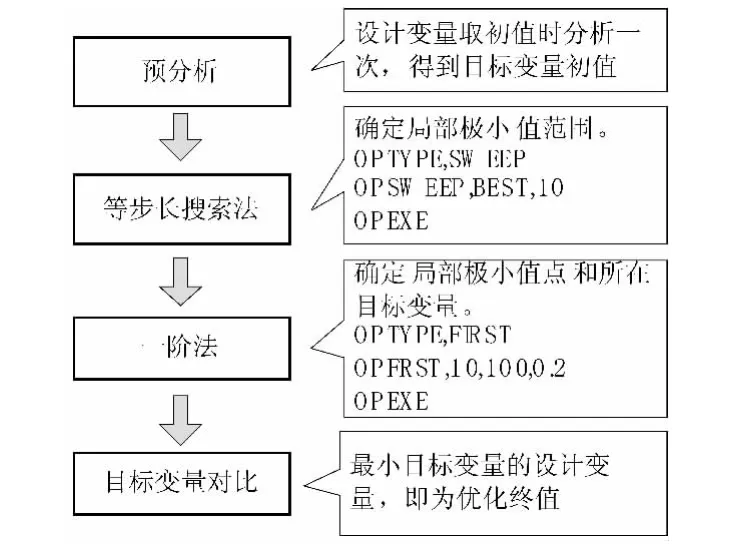
圖5 優(yōu)化流程Fig.5 Flow chart of optimization

3 優(yōu)化結(jié)果分析

對(duì)4組實(shí)驗(yàn)提供的動(dòng)態(tài)模量數(shù)值進(jìn)行優(yōu)化后得到等效模量常值Ea，如表2所示。

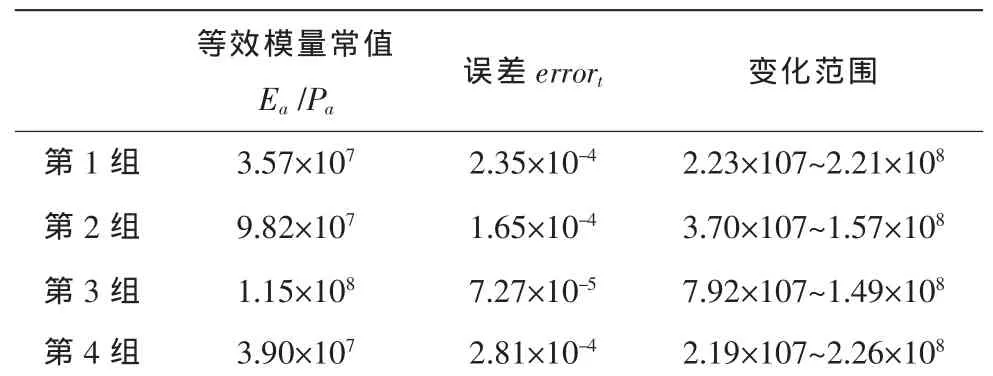
表2 等效模量常值及其誤差Tab.2 Errors and range of dynamic modulus

相比表1，經(jīng)等效之后，輸入功率誤差比任取更小。且隨著動(dòng)態(tài)模量變化范圍越窄，相應(yīng)誤差越小。

分別代入等效模量常值進(jìn)行分析，得到等效后的輸入功率，并與動(dòng)態(tài)模量的輸入功率對(duì)比，如圖6~9所示。

由圖6~9知，本文的等效方法所得的4種數(shù)據(jù)的等效模量常值下的輸入功率，在考察頻段內(nèi)，分別與該4種材料的動(dòng)態(tài)模量下的輸入功率比較，結(jié)果都較為接近，能很好的反映該頻段內(nèi)受激勵(lì)點(diǎn)的能量特性。對(duì)于模量變化范圍窄的動(dòng)態(tài)模量，等效作用不明顯。反之，對(duì)模量變化范圍寬的動(dòng)態(tài)模量，等效作用更顯著。

4 結(jié)論

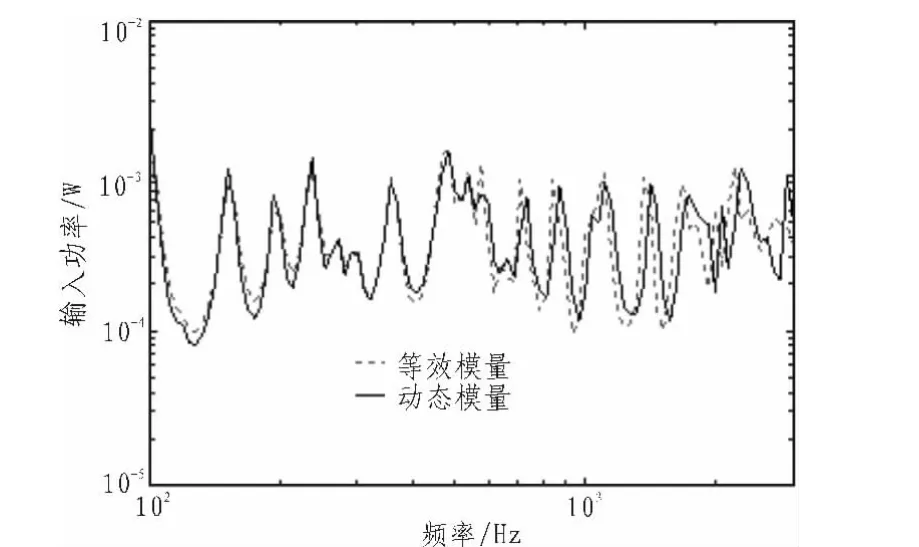
圖6 第1組等效結(jié)果Fig.6 Result of equivalence for the 1st time

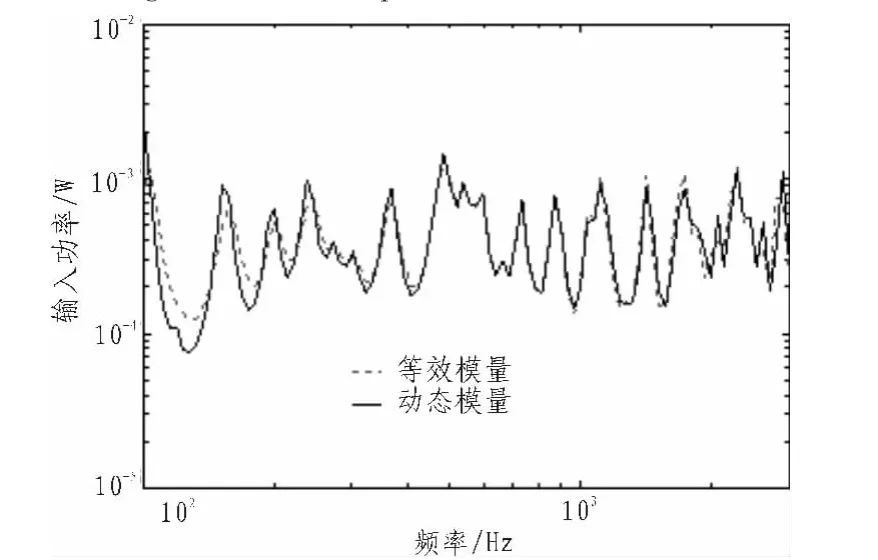
圖7 第2組等效結(jié)果Fig.7 Result of equivalence for the 2nd time

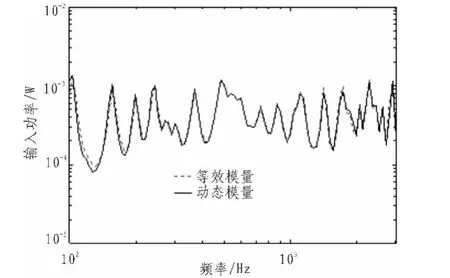
圖8 第3組等效結(jié)果Fig.8 Result of equivalence for the 3rd time

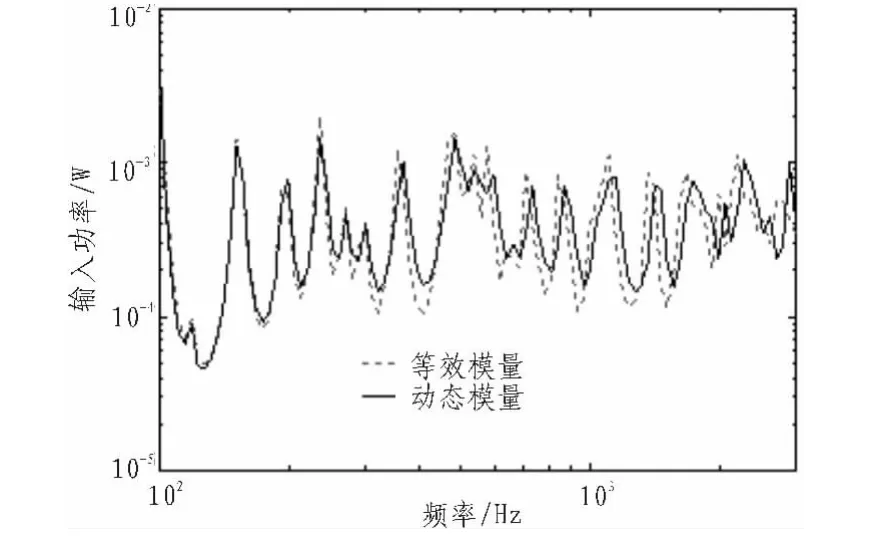
圖9 第4組等效結(jié)果Fig.9 Result of equivalence for the 4th time

本文提出一種基于能量等效原則，將粘彈性材料的動(dòng)態(tài)楊氏模量等效為楊氏模量常值方法。利用有限元軟件的優(yōu)化模塊，從動(dòng)態(tài)模量數(shù)據(jù)中獲取了最接近動(dòng)態(tài)模量下的等效模量常值，以用于特定結(jié)構(gòu)的軟件和數(shù)值仿真計(jì)算，為工程應(yīng)用提供便利。

[1]劉棣華.粘彈阻尼減振降噪應(yīng)用技術(shù)[M].北京:宇航出版社,1990.

[2]胡衛(wèi)強(qiáng),王敏慶,盛美萍,等.阻尼材料動(dòng)態(tài)性能參數(shù)的寬頻帶測(cè)試研究[J].機(jī)械科學(xué)與技術(shù)，2007.29(11):1425-1428.HU Wei-qiang,WANG Min-qing,SHENG Mei-ping,et al.Broadband measurement of dynamic performance parameters of damping materials[J].Mechanical Science and technology for Aerospace Engineering,2007,29(11):1425-1428.

[3]姚德源,王其政.統(tǒng)計(jì)能量分析原理及其應(yīng)用[M].北京:北京理工大學(xué)版社,1995.

[4]Cremer L M,Heckl,Petersson B.A.T.Structure-borne sound[M].Berlin:Springer,2005.

[5]任輝啟.ANSYS7.0工程分析實(shí)例詳解[M].北京:人民郵電出版社,2003.

[6]Taylor F J,Mellott J.Digital filters:principles and applications with MATLAB[M].New York:Wiley-Blackwell,2011.