超聲速二次喉道擴壓器流動特性的數值模擬

孔令軒，宋文艷

（西北工業大學 動力與能源學院，陜西 西安 710072）

超聲速擴壓器位于風洞試驗段之后，相當于倒置的拉法爾噴管，超聲速氣流通過收縮段減速增壓，在二次喉道處馬赫數略大于1，然后通過擴張段繼續減速增壓。由于二次喉道處氣流速度遠低于試驗段出口，經過激波串之后總壓損失較小，這樣能夠降低風洞運行壓比，所以直接關系著風洞運行的經濟性[1]；二次喉道中激波串的位置可以向上下游移動，反壓升高時，激波串向上游移動，二次喉道的存在使得風洞能夠在較廣的范圍內正常工作。

然而二次喉道擴壓器實際起動過程中存在超聲速流在逆壓梯度環境下轉化成亞聲速，存在激波-邊界層-流動分離之間的相互作用，管道內減速-加速-再減速的激波串結構[2]呈現出非常復雜的特點，理論計算方法無法準確地描述該流動過程，試驗方法亦有其局限性并且成本較大。利用CFD數值模擬能夠很好地分析這一過程。

針對超聲速擴壓器內流動現象，Carroll[3]通過試驗方法測量了流場中速度分布并采用多種數值數值方法進行了模擬；Neumann[4-5]等人在探索風洞設計過程中對超聲速內流激波串、激波串和邊界層干涉現象進行了理論和數值研究，對激波串現象進行了初步的闡釋；Matsuo[6]等人對內部流動中激波鏈和偽激波鏈生成的機理和過程進行了深入的研究，對氣流經過激波鏈壁面壓力、中心壓力及其他參數變化做了細致的分析，發現邊界層多次分離，超聲速區域通過粘性剪切層過渡到亞聲速現象，將激波串和混合區域統稱為偽激波。

在二次喉道流場的數值模擬中，Bartosiewiez[7-8]對多種湍流模型進行了研究，發現RNG k-ε模型和sst k-ω模型對流場的模擬結果與試驗數據最接近，而sst k-ω在模擬氣流之間的混合獲得了更好的效果；Jacobs[9-10]針對T4激波風洞中噴管起動過程進行了非定常的數值模擬，同試驗采集數據對比發現，數值模擬能夠準確地描述風洞起動過程中流場變化。

本文針對某超聲速地面試驗設備，使用流體力學軟件Fluent進行求解，得到了從設備噴管-二次喉道擴壓器充分發展流場，比較了二次喉道長徑比L/D參數對起動特性的影響，非定常方法模擬真空箱壓力逐漸升高，分析了設備的抗反壓性能。

1 計算方法和計算模型

1.1 數值方法

本文采用Fluent軟件通過有限體積法求解二維軸對稱雷諾平均Navier-Stokes方程；湍流模型選用兩方程的SST kω模型；空間上選用隱式耦合的二階迎風離散格式；設備噴管入口采用壓力進口條件；壁面使用無滑移壁面；在計算時考慮了變比熱的影響；非穩態過程采用雙時間步計算格式，

非定常時間項采用一階隱式格式[11－12]。

1.2 計算模型和網格

如圖所示，計算模型包含設備噴管、試驗段、二次喉道擴壓器、真空箱，為典型的二維軸對稱結構。使用ICEM－CFD商用軟件對對象區域生成結構化網格，在近壁面，噴管處，二次喉道，剪切層以及流場變化劇烈處進行網格加密。

圖1 計算模型及網格Fig．1 Model and computational mesh

1.3 計算方法驗證

由于二次喉道中激波串與邊界層流動特點復雜，對文中計算方法使用前人試驗結果進行驗證。如圖2為Bartosiewiez和Desevaux進行超聲速引射器試驗，在引射器二次流[13]為零時，即為二次喉道擴壓器。試驗中噴管出口氣流Ma=2．3，總壓Pt=4．0 atm，總溫 Tt=300 K，出口反壓 Pamb=1．0 atm。試驗中使用毛細管得到了流場中心線上的靜壓分布，如圖所示為計算結果同試驗結果對比分析，壓力分布波峰和波谷符合良好，發現文中計算方法對激波串能夠較為準確地捕捉，對于二次喉道擴壓器的流場能夠很好地模擬。

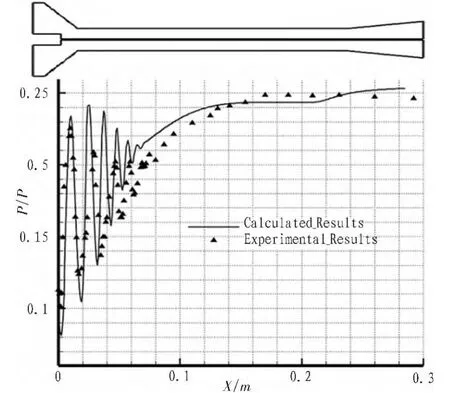
圖2 基于Desevaux引射器試驗算例驗證Fig．2 Verification of simulation based on Desevaux’s ejector experiment

1.4 邊界條件及初始條件

風洞起動之前使用抽吸設備將試驗段－二次喉道擴壓器－真空箱中壓力抽到 Pini=1．6 kPa，Tini=300 K；來流總壓為Pt=1．4 MPa，來流總溫Tt=1 650 K，在初始時刻高溫高壓氣流從Ma=6的設備噴管進入試驗設備。

2 二次喉道擴壓器流動特性分析

風洞起動時，閥門打開，高溫高壓空氣向下游流動，首先在第一喉道（設備喉道）處形成超聲速流，超聲速流向下游推進，如果壓比不夠，氣流通過正激波變成亞聲速流；

隨著上游壓力增加，起動激波向下游推進，這時波前M數增加，流動損失也增大；當起動激波推到試驗段下游，試驗段中來流為均勻的超聲速氣流，則可進行試驗。

圖3所示為流場充分發展時馬赫數在中心軸線上的分布，該時刻真空箱內反壓為30 kPa。從試驗段到擴壓器整個通道中為充分發展的超聲速氣流；在放置試驗模型的溢流擴壓器中，形成自由射流菱形區，如圖5，一定區域內導流錐截面上皆為均勻高速氣流；自由射流在噴管出口處膨脹加速，超聲速主流對高空倉中溢流進行引射，保證試驗段內保持低壓環境；超聲速氣流經過收縮段，馬赫數下降壓力上升，二次喉道中膨脹波壓縮波交替反射，所以中心處馬赫數出現波動式下降，然而這一過程中壁面壓力如圖4所示并沒有大幅提升；在二次喉道擴壓器出口，出現了激波串的典型結構，壁面壓力單調上升，而中心壓力大幅波動式上升，軸線處馬赫數波動式下降；如圖5中馬赫數等值線圖所示，在擴壓器擴張段，第一道斜激波同邊界層作用誘發邊界層分離，每經過一次壓縮－膨脹結構，附面層分離加劇，亞聲速區域增加，最終經過混合區域，全部轉化為亞聲速。

值得注意，在此階段整個二次喉道中皆為超聲速氣流，在擴張段內通過激波串減速增壓，此時二次喉道擴壓器工作在超臨界狀態。在超臨界狀態下，二次喉道擴壓器工作具有很大的抗反壓裕度；隨著真空箱內反壓的增大，激波串向前移動，在進入二次喉道之后，設備對于反壓變化的響應迅速增大，反壓的較小變化能夠引起二次喉道內激波串大幅度移動；當反壓繼續增大之后二次喉道擴壓器處于亞臨界狀態，此時，不管是來流變化還是反壓的變化都會輕易地使試驗段內流場發生劇烈變化，不再適宜進行發動機試驗。這也正是等截面的擴壓器增壓效果較變截面擴壓器好，但是穩定性不如變截面擴壓器。

3 不同構型二次喉道擴壓器性能比較分析

數值比較二次喉道長徑比L/D=7，L/D=7．5兩種構型下的擴壓器，使用非穩態計算方法模擬隨著時間真空箱中壓力逐漸增大，擾動向前傳播的過程，如圖6所示為不同時刻，反壓由低到高的過程中，兩種構型馬赫數云圖比較。Time1～Time3過程為二次喉道擴壓器起動過程，此時真空箱內反壓極低；Time3～Time6 對應反壓依次為 30 kPa、36 kPa、40 kPa、42 kPa。可以看出自二次喉道擴壓器起動之后，如前文所述，在超臨界狀態下工作范圍很廣，激波串位于擴壓器擴張段內，可以極大限度內防止反壓對試驗區域產生干擾；而一旦激波串進入二次喉道，即臨界狀態下，反壓變化迅速響應到上游流場。將激波串即將進入二次喉道處時反壓稱為安全反壓。

圖3 馬赫數在軸線上的分布Fig.3 Mach number distribution along axis

圖4 壓力在壁面及軸線方向上的分布Fig.4 Static pressure distribution along wall and axis

圖5 自由射流流線及擴壓器馬赫數等值線Fig.5 Streamline of free jet and Mach number distribution in diffuser

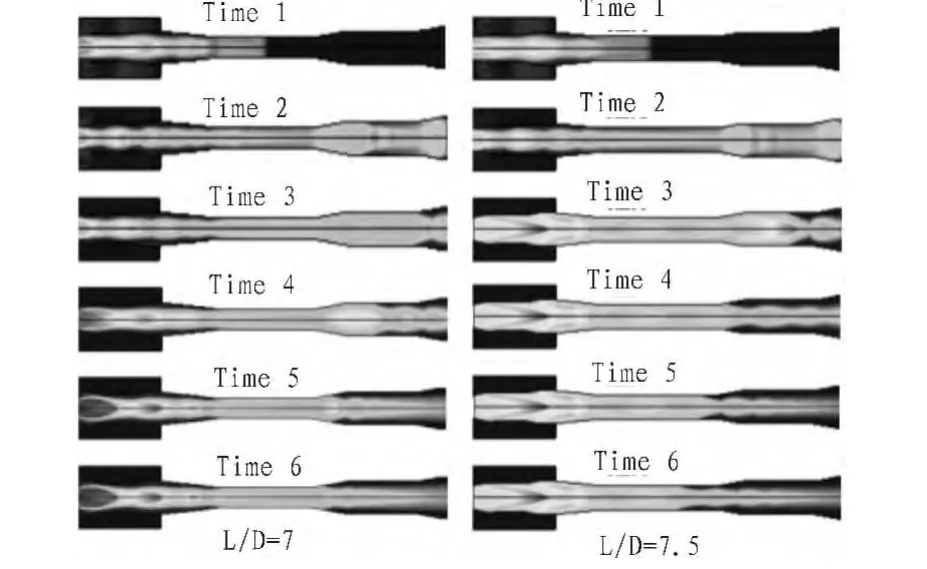
圖6 兩種構型不同反壓下流場內馬赫數云圖Fig.6 Mach number distribution contour under different back pressure of two configurations

二次喉道在風洞起動過程中是壅塞風洞第一個截面，根據質量守恒方程可以得到風洞起動二次喉道最小面積為（工質為空氣）。式2擴壓器的效率定義為實際壓力恢復值同氣流經過一道正激波的理想壓力恢復值之比。

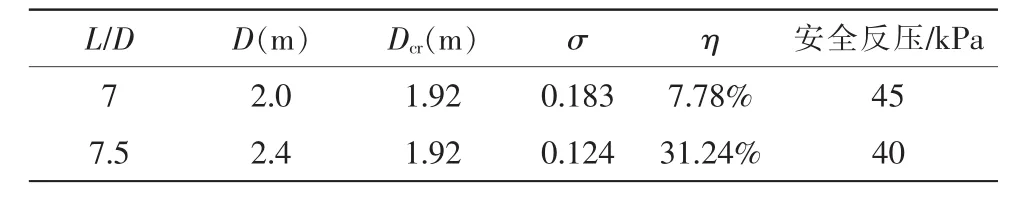
表1 兩種構型擴壓器參數對比Tab.1 Parameters comparison of two configurations

從圖6中比較發現，當長徑比為7.5時，二次喉道擴壓器以及試驗段溢流擴壓器內為充分發展的超聲速氣流；而長徑比為7時，從設備起動至充分發展直到反壓逐漸升高的過程中，在試驗區域附面層發生嚴重的分離，溢流擴壓器壁面附近出現大面積的亞聲速區域，自由射流區域氣流均勻性很差，在這樣的工況下明顯無法正常進行試驗。通過表1看出兩種構型下二次喉道直徑均滿足風洞正激波理論最小起動面積，兩種構型較最小起動直徑分別多出4%和25%，可見粘性補償在二次喉道擴壓器設計中尤為關鍵，較大余量的粘性補償更易于風洞起動。

由于附面層的分離，L/D7擴壓器效率大大下降，靠近壁面大面積的低速區導致總壓恢復系數亦高于L/D7.5構型。如果忽略試驗段處的差異，發現在相同背壓條件下，二次喉道直徑更小，激波串處于更下游的位置，安全反壓更高。即二次喉道直徑增大，起動性能更好，但是抗反壓能力變差。

超聲速氣流要先經過斜激波系才能減速到低超聲速，這取決于收縮部分的收縮角和長度，斜激波系可以是單斜激波形式，也可以是多斜激波形式。先經過一系列斜激波使試驗段的超聲速減速到低超聲速，然后再經過正激波變成亞聲速的總壓損失低于氣流直接經過正激波減速時的壓力損失。

L和D兩個特征尺寸對擴壓器效率和流動損失有著重要的影響，然而D小容易發生風洞不起動現象，D大設備抗反壓性能變差且所需壓比較高。增大L/D一定范圍內能提高擴壓器效率。

4 結束語

本文使用經過驗證的計算方法，對于超聲速發動機地面試驗設備進行了數值模擬，得到試驗段-二次喉道擴壓器充分發展的流場，使用非定常方法模擬反壓升高過程中擴壓器流動特性。研究表明：二次喉道擴壓器工作在超臨界狀態時具有較大的抗反壓裕度，但是效率較低；二次喉道設計中粘性補償關系到風洞的起動性能，但是直徑增加導致抗反壓能力下降；二次喉道長徑比對擴壓器效率影響較大。

[1]Anderson J D.Modern Compressible Flow:With Historical Perspective（3rd ed）[M].New York:McGraw-Hill，2003.

[2]李樺，范曉檣，丁猛.超聲速擴壓器中激波串結構的數值模擬[J].國防科技大學學報，2002（24）:18-21.LI Hua，FAN Xiao-qiang，DING Meng.Numerical simulation of the shock train structure in the supersonic diffuser[J].Journal of National University of Defense Technology，2002（24）:18-21.

[3]Carroll BF，Dutton JC.Multiple normal shock wave/turbulent boundary-layer interactions[J].Journal of Propulsion Power，1992，8（2）：441-448.

[4]Neumann E P，Lustwerk F.Supersonic diffusers for wind tunnels[J].J Appl Mech，1949，16（2）:195-202.

[5]Neumann E P，Lustwerk F.High efficiency supersonic diffusers[J].J Aeronaut Sci，1951，18（6）:369-374.

[6]Matsuo K，Miyazato Y，Kim H D.Shock train and pseudo-shock phenomena in internal gas flows[J].Progress in Aerospace Sciences，1999：33-100.

[7]Bartosiewicz Y，Aidoun Z，Desevaux P，et al.Numerical and experimental investigations on supersonic ejectors[J].International Journal of Heat and Fluid Flow，2005.

[8]Bartosiewicz Y，Aidoun Z，Desevaux P，et al.CFD-Experiments Integration in the Evaluation of Six Turbulence Models for Supersonic Ejectors Modeling [R].Conference Proc.，Integrating CFD and Experiments， Glasgow， UK.， 2003.

[9]Jacobs P A.Simulation of transient flow in a shock tunnel and a high Mach number nozzle[R].NASA-CR-187606，1991.

[10]Jacobs P A.Transient，hypervelocity flow in an axisymmetric nozzle[R].NASA-CR-187496，1991.

[11]張小慶，樂嘉陵.脈沖式燃燒風洞起動特性數值研究[J].航空動力學報，2008，23（9）:1568-1572.ZHANG Xiao-qing，LE Jia-ling.Numerical study on the starting characteristics of the pulse combustion wind tunnel[J].Journal of Aerospace Power，2008，23（9）:1568-1572.

[12]Fluent Inc.Fluent version user’s guide[M].Lebanon， USA:[s.n]2005.

[13]Computational Fluid Dynamic Modeling of Pseudoshock Inside a Zero-Secondary Flow Ejector[J].AIAA Journal，2004.

[14]王新月.氣體動力學基礎[M].西安：西北工業大學出版社，2006.

[15]伍榮林，王振羽.風洞設計原理[M].北京：北京航空學院出版社，1985.