適用于電算的設計洪水過程線放縮方法

王艷芳，吳明官，曹 越

(黑龍江省水利水電勘測設計研究院，哈爾濱150080)

適用于電算的設計洪水過程線放縮方法

王艷芳，吳明官，曹 越

(黑龍江省水利水電勘測設計研究院，哈爾濱150080)

目前，在水利水電工程水文分析計算中，常用同頻率法放縮設計洪水過程線。這是一項比較繁瑣而且經驗性比較強的計算工作，不容易電算化。多年來，許多人為了把既繁瑣又帶有經驗性的手算工作，實現為電算化，進行了不懈的探索和研究。筆者在大量使用同頻率法放縮設計洪水過程線中，探討了比較適用于電算的洪量控制法、逐次K值逼近法、鮑爾明法的使用范圍及修勻方法，供水文界同行們參考。

洪量控制法;逼近法;鮑爾明法;設計洪水過程線;方法比較

1 計算問題

目前，如何推求一定設計頻率的洪水過程線，并無完善的方法。一般是將典型洪水過程線加以放縮，使放縮后的洪水過程線中的洪峰流量和各時段洪量均達到設計要求，這就是常用的同頻率法放縮的設計洪水過程線。對典型洪水過程線的放縮，有同倍比和同頻率兩種方法。其中同頻率法較適應多種防洪工程的特性，目前大、中型水庫工程規劃設計中，主要是采用此法。下面簡述同頻率法推求設計洪水過程線的計算問題。

1.1 選擇典型洪水過程線

選擇峰高量大的實測洪水過程線作為典型，因為這種情況是比較接近于設計條件下稀遇洪水的情況。若峰高量大的過程線較多時，則應從中選擇較易出現的具有代表性的典型。還可以選擇峰形比較集中，并且主峰靠后的過程線作為典型。另外，選擇典型洪水過程線時，應該注意一點就是典型洪水過程線各時段的最大洪量應該是長包短，即最大3 d洪量包最大1 d洪量、最大7 d洪量包最大3 d洪量、最大15 d洪量包最大7 d洪量等。否則各時段放縮倍比的銜接處會出現K值交錯的現象。

1.2 放縮倍比計算

洪峰流量的放縮倍比:

各時段洪量的放縮倍比:

式中:Qp為設計洪峰流量，m3/s;Qm為典型洪峰流量，m3/s;Wpi為最大i日設計洪量，m3;Wi為最大i日典型洪量，m3。

1.3 放縮典型洪水過程線

依據典型洪水過程線和各時段放縮倍比，求得初始的設計洪水過程線。在典型洪水過程線的放縮過程中，由于鄰近時段銜接處放縮倍比K值不同，所以在放縮后的洪水過程線交界處出現不連續的突變現象，使設計洪水過程線呈階梯形。

1.4 修勻設計洪水過程線

依據典型洪水過程線形狀和初始的設計洪水過程線及設計洪量，修勻放縮后的設計洪水過程線。修勻過程線的目標為各時段洪量要滿足設計洪量，而且設計洪水過程線形狀與典型洪水過程線相似。

2 適用于電算的放縮方法

多年來，在大、中型水庫工程規劃設計工作中，曾采用許多算法推求過同頻率設計洪水過程線，歸納起來較適用于電算的設計洪水過程線放縮方法為洪量控制法、逐次K值逼近法和鮑爾明法。

2.1 逐級洪量控制法

此法主要靠控制逐級洪量來達到修勻設計洪水過程線的目的。這種方法的基本思路如下:

2.1.1 計算放縮倍比

按上述的洪峰流量及各時段洪量放縮倍比計算公式，計算 K0、K1、K2、K3……Km。

2.1.2 K值過程線

采用線性插值法推求放縮倍比K值過程線。用公式表示為

峰前K值:

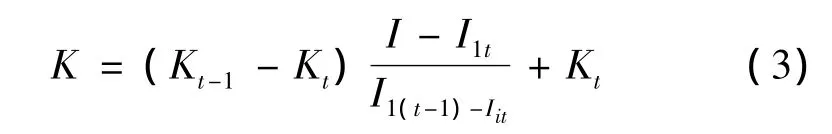
式中:t=m、m － 1、m － 2……3、2、1;I=0、1、2、3……n1(峰前時段總數)。

峰后K值:

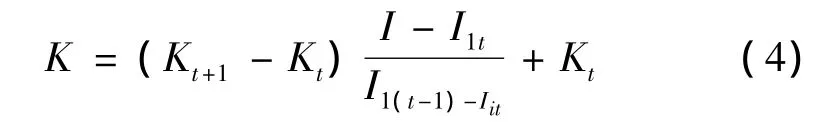
式中:t=0、1、2……m(放縮倍比K值個數);I=n1、n1+1、n1+2……n(洪水過程線時段總數);K(t)為各時段放縮倍比K值;I1(t)為各時段最大洪量的起始時間(時段數);I(t)為各時段最大洪量的終止時間(時段數)。

2.1.3 初始過程線

由典型過程線和K值過程線相乘后，求得第一次初始設計洪水過程線，該過程線的形狀較接近于典型過程線，但各時段洪量與設計洪量相差較大。

2.1.4 逐級洪量控制

初始放縮后的洪水過程線，如果不滿足各時段設計洪量的允許精度要求時，計算機自動地進行修正計算［1］。修正計算的基本原則就是控制逐時段的設計洪量，即每次計算的各時段洪量與設計洪量相比，如果ABS(1－W計/Wp)＜δ規定的精度時，則滿足設計要求，否則先計算:

式中:ΔW為各時段洪量的誤差;Ht為各時段洪量的時段數;C為洪量單位系數(104m3或106m3或108m3);Δt為洪水過程線的時段長，h;ΔQ為修正后的平均流量，m3/s。

然后在ΔH的洪量時段內平均分配其ΔQ(加或減)，這樣反復地進行修正計算，直到滿足設計洪量的精度要求為止。最終放縮后的設計洪水過程線，如果在某一時段內出現鼓包(上凸)或下凹的現象時，本次改進的方法是在該時段內應采取放寬控制精度的措施進行修勻計算，其它時段根據設計洪水過程線的具體形狀適當地調整其各時段洪量的控制精度，直到修勻為止。實際上，手算時也同樣出現這種情況，只不過無意中為了修勻設計洪水過程線放寬了該時段的控制精度而已。本法的主要優點是計算速度快，各時段洪量的相對誤差控制得好，精度較高，但是有時局部地方仍出現鼓包(上凸)或下凹的現象，出現這種情況時，人工稍加修勻就可以了。

2.2 逐次K值逼近法

這種方法主要靠各時段放縮倍比K值的逐次逼近來達到修正設計洪水過程線的目的。此方法與逐級洪量控制法有本質上的區別，它的基本思路如下:

2.2.1 計算放縮倍比

同樣地先計算放縮倍比 K0、K1、K2、K3……Km。

2.2.2 初始過程線

也同樣地由K值過程線和典型過程線相乘后，第一次求得初始的設計洪水過程線。

2.2.3 逐次K值逼近

把第一次放縮后的初始的洪水過程線再作為典型過程線，重新計算放縮倍比，然后再用新的K值過程線放縮第一次放縮后的洪水過程線，這樣又得到了第二次放縮后的洪水過程線，這次的放縮倍比K值比前一次更接近于1。如果迭代后的放縮倍比K值接近于規定的精度要求，那么可以認為該次典型過程線就可以作為設計洪水過程線。否則再把第二次放縮后的設計洪水過程線作為典型過程線，再計算放縮倍比K值，然后進行放縮第3次設計洪水過程線，這樣反復地進行迭代計算，直到滿足max(K－1)＜δ規定的精度要求為止。

本法的主要優點是能夠較好地控制設計洪水過程線的形狀與典型過程線相符，算法比較簡單，很容易在計算機上實現，但是計算速度較慢，各時段的洪量控制精度較差，能滿足規定的精度要求。

2.3 鮑爾明法

本法是華東水利設計院鮑爾明同志提出的同頻率放縮設計洪水過程線的方法。下面簡單介紹該方法的計算公式:

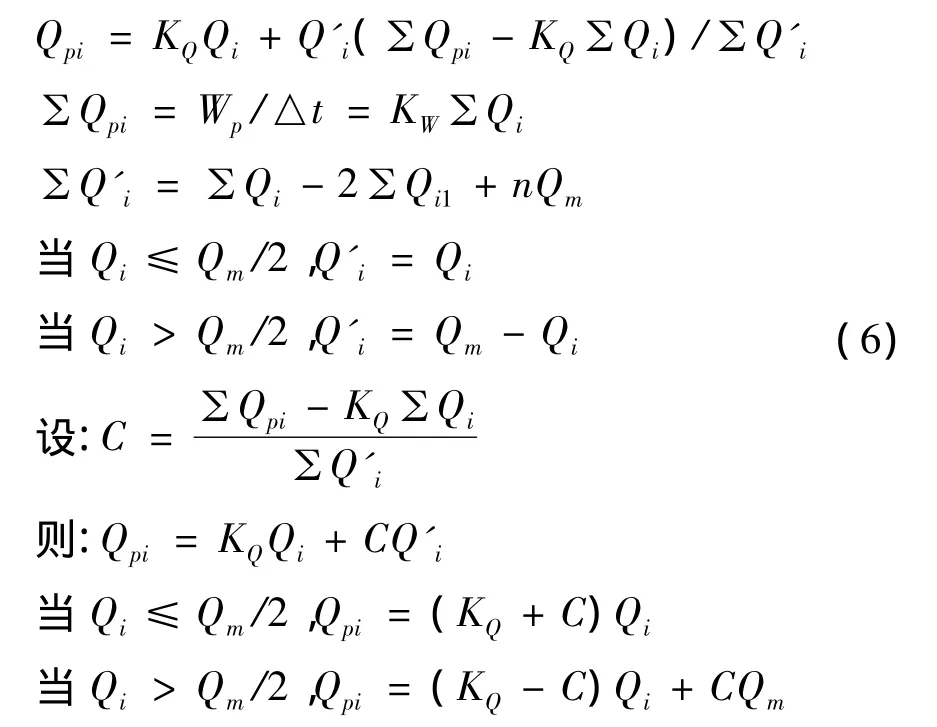
式中:Qpi為設計洪水過程線的流量;Qi為典型洪水過程線的流量;Wp為某頻率的設計洪量;KQ、Kw分別表示洪峰、洪量倍比系數;Qm、Qpm分別表示典型、設計洪峰流量;ΣQi1為Qi＞Qm/2的Qi之和;n為Qi＞Qm/2的Qi的個數;ΣQi為典型洪水過程線的時段流量之和;△t為時段長。

本法的主要優點是在計算機上容易實現，計算速度較快，但是各時段洪量的相對誤差無法控制，精度有時較差，能滿足設計要求，有時局部地方也出現鼓包或下凹的現象。

3 方法比較與討論

上述介紹的適用于電算的3種方法，從30多a的運用情況來看，有30%左右是很滿意的成果;40%左右是較滿意的經過適當修勻的成果;25%左右是較差的修改典型后修勻的成果;5%左右是很差的基本上不能采用的成果。對同一例子來說，上述的3種方法，有時洪量控制法好，有時k值逼近法好，又有時鮑爾明法好，而沒有一種方法是絕對優勢的，這3種方法各有其優缺點，各有各的使用條件，情況比較復雜，所以不能簡單地肯定或否定某一種方法，應該把這3種方法都編入計算機程序中，選擇其較優的計算成果。如果這3種方法計算的成果均不理想時，建議試用如下的修勻方法。

3.1 分析各時段洪量倍比關系

先分析典型洪水過程線最大1 d洪量與最大3 d洪量倍比、最大3 d洪量與最大7 d洪量倍比、最大7 d洪量與最大15 d洪量倍比關系等，即K典=Wi/Wi+1。

再分析各設計洪量的相鄰時段洪量間倍比關系，即

式中:K典為典型的相鄰時段洪量比值;K設為設計的相鄰時段洪量比值;Wi為典型的最大1、3、7、15 d等洪量;Wpi為設計的最大 1、3、7、15 d等洪量。

如果典型與設計的相鄰時段洪量比值相等或接近(K典≈K設)，那么典型過程線放縮的效果良好，一般不需要修勻過程線，否則放縮后的設計洪水過程線效果均不理想。實際上K典與K設相差較大時，手算的設計洪水過程線的效果也不好，遇到這種情況時手算比電算更靈活，但是手算的修勻工作量很大。

3.2 修改典型過程線

從大多數設計洪水過程線的放縮成果來看，如果ABS(K典－K設)≤0.05，則不需要修改典型過程線，也能達到修勻設計洪水過程線的目的，否則按下面的方法修改典型過程線后再放縮設計洪水過程線。

式中:Qi、Q'i分別為修改前、后的典型過程線流量;Qi、Q'i分別為修改前、后的最大1、3、7、15 d等洪量;K設相鄰時段設計洪量的比值。

根據原典型過程線和修改后的典型過程線，修勻其Qt'～t過程線。修勻后的典型過程線各時段洪量倍比盡量滿足設計洪量的倍比，而且典型過程線形狀也盡量保持原典型過程線的樣子。

3.3 放縮設計洪水過程線

根據修勻后的典型過程線和各時段設計洪量，采用上述的3種方法放縮設計洪水過程線。另外，放大較稀遇頻率的設計洪水過程線時，由于典型過程線各時段洪量與設計洪量往往相差懸殊，所以，先放縮接近典型洪量的設計洪水過程線，然后以放縮后的設計洪水過程線再逐級放縮其它設計洪水過程線，這樣的計算效果比單用一個典型過程線放縮的成果好。

［1］肖義，郭生練，方彬，劉攀.設計洪水過程線方法研究進展與評價［J］.水力發電，2006(07):64－66.

TV122.3

B

1007－7596(2014)07－0055－03

2013－12－12

王艷芳(1982－)，女，河南焦作人，工程師;吳明官(1955－)，男，黑龍江哈爾濱人，教授級高級工程師;曹越(1980－)，男，遼寧興城人，工程師。