僅發送者知道通道信息的可控概率隱形傳態
夏立新 李 超 賈文濤
(河南科技大學 物理工程學院,河南 洛陽 471023)
僅發送者知道通道信息的可控概率隱形傳態
夏立新 李 超 賈文濤
(河南科技大學 物理工程學院,河南 洛陽 471023)
采用推廣測量法,在僅發送者Alice知道部分糾纏GHZ態通道信息的條件下,提出了實現可控概率隱形傳態的方案。
GHZ態;糾纏交換;推廣測量;概率隱形傳態
0 引 言
量子隱形傳態是一種全新的通信方式,它是在量子糾纏和經典信息的幫助下,將甲地的某一量子系統(粒子)的未知量子態在乙地的另一量子系統(粒子)上還原出來。量子隱形傳態,在1993年由Bennett等首次提出[1],直到1997年才由Bouwmeester等[2]用實驗所驗證。目前,量子隱形傳態已成為量子信息領域研究的熱點之一。國內外許多研究組已提出了利用Bell態、GHZ態、W態、團簇態等作為量子通道的量子隱形傳態方案[3-8],這些方案中接收者Bob不僅需要引入一個輔助粒子,而且也需要完全知道非最大糾纏態的信息。最近,Wei等提出了一個新的方案[9],僅發送者Alice知道信道---部分糾纏Bell態---的信息時,提出了實現了概率隱形傳態的方案。該方案對量子隱形傳態的研究和發展是非常有意義的。
本文將采用Wei的方法,在僅發送者Alice知道部分糾纏Greenberger-Home-Zeilinger(GHZ)態通道信息的條件下,提出了實現可控概率隱形傳態的方案。
本文組織如下:在第1節中,構造可控的量子通道;在第2節中,在僅發送者知道部分糾纏GHZ態信道的條件下,提出實現可控概率隱形傳態的方案。最后,在第3節中,給出了全文總結。
1 可控量子通道的建立
我們首先介紹通過糾纏交換[10]建立一個可控的量子通道[11]。假設發送者Alice、接收者Bob和控制者Clair事先共享一個部分糾纏GHZ態,其中Alice擁有粒子1,Bob擁有粒子 2,Clair擁有粒子 3。為了不失一般性,部分糾纏GHZ態可表示如下

其中,粒子4屬于Alice,粒子5屬于Clair。
若Clair同意幫助Alice和Bob完成隱形傳態,則他必須先對粒子3和粒子5進行適當的操作,使得粒子1、2和4相互糾纏,實現糾纏交換,并使之作為量子通道。這五個粒子的初態可表示為
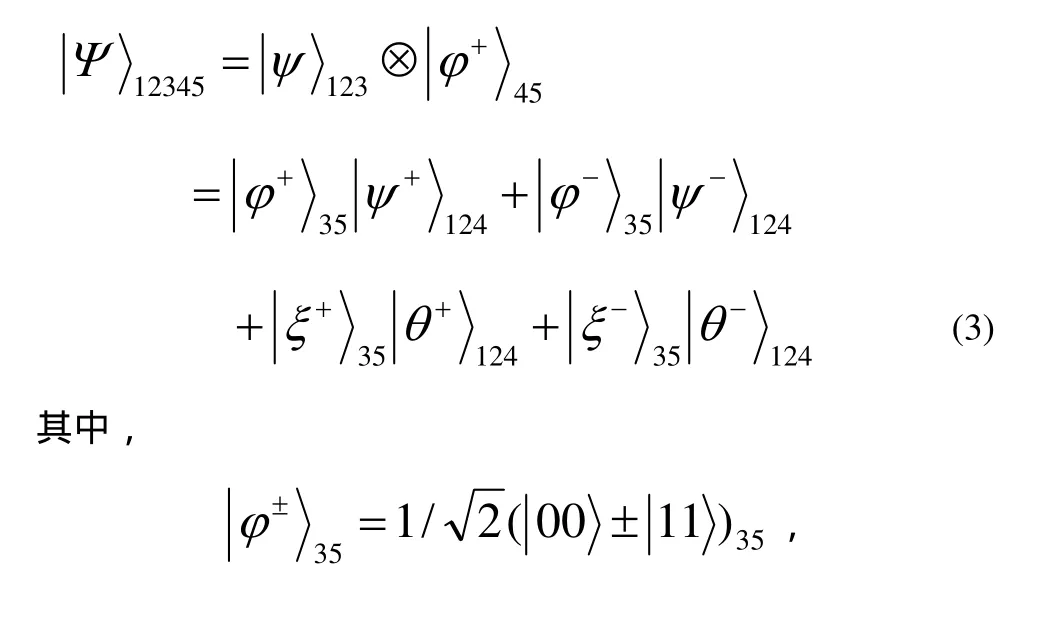

此時,發送者 Alice和 Bob此時共享一個三粒子糾纏態,其中Alice擁有粒子1和4,Bob擁有粒子2。若Clair不同意開通Alice和Bob之間的通道,則由于缺少Clair的操作,Bob不能僅根據Alice的測量得到糾纏態(4)。從上可知,Clair在量子通道建立過程中是不可或缺的。這樣,我們通過糾纏交換建立了一個可控的量子通道。
2 僅發送者知道量子通道信息的隱形傳態
在典型方案[9]中,接收者Bob要知道部分糾纏態的參數(a和b)才能構造對粒子3和輔助粒子P進行相應的幺正變換UF操作。這表明,對于經典方案,僅發送者Alice知道部分糾纏態全部信息的情況下,概率隱形傳送是不能完成的。為了克服這個不足,下面我們采用Wei的方法實現隱形傳態。
系統處于(3)式的量子態,可表示為

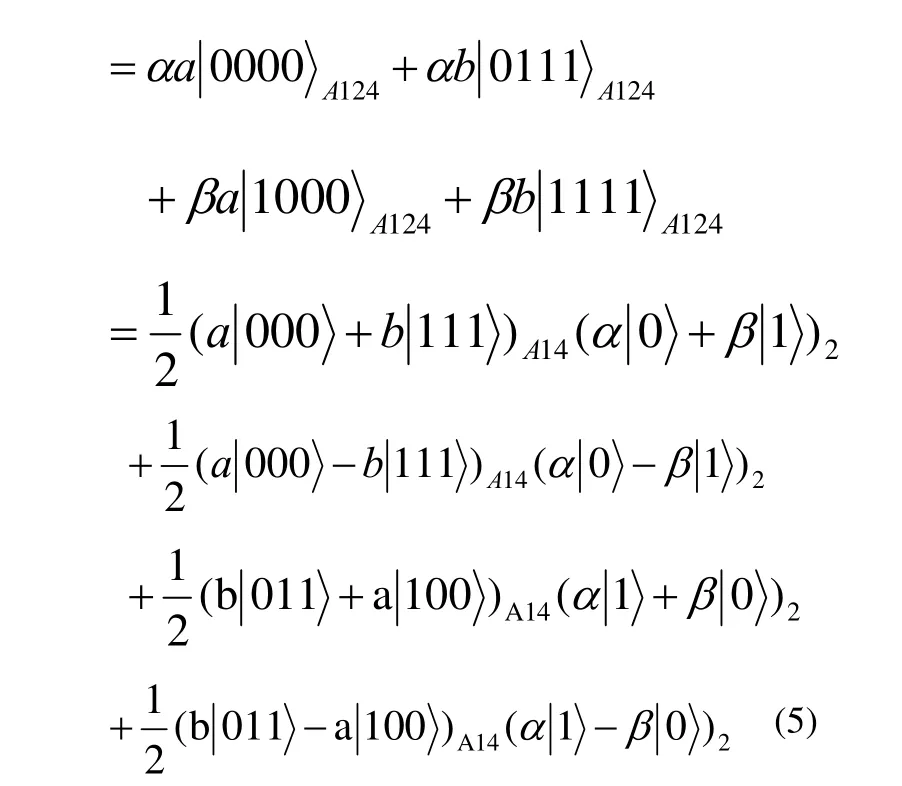
只有發送者 Alice知道部分糾纏態全部信息(a和b)時,她可構造對系統進行操作的5個推廣算符Mi(i=0, 1, 2, 3, 4),可給出如下

接著,Alice對粒子A、1和4進行測量,并且通過經典信息告訴Bob測量結果。為了重現初態,Bob要在2粒子上進行相應的幺正變換UG。表2是對粒子A、1和4進行測量后的結果,以及要對2粒子所進行的幺正變換UG。計算可得,量子隱形傳送總的成功概率是。如果即,當量子通道是最大糾纏態構成時,總成功概率可為1。
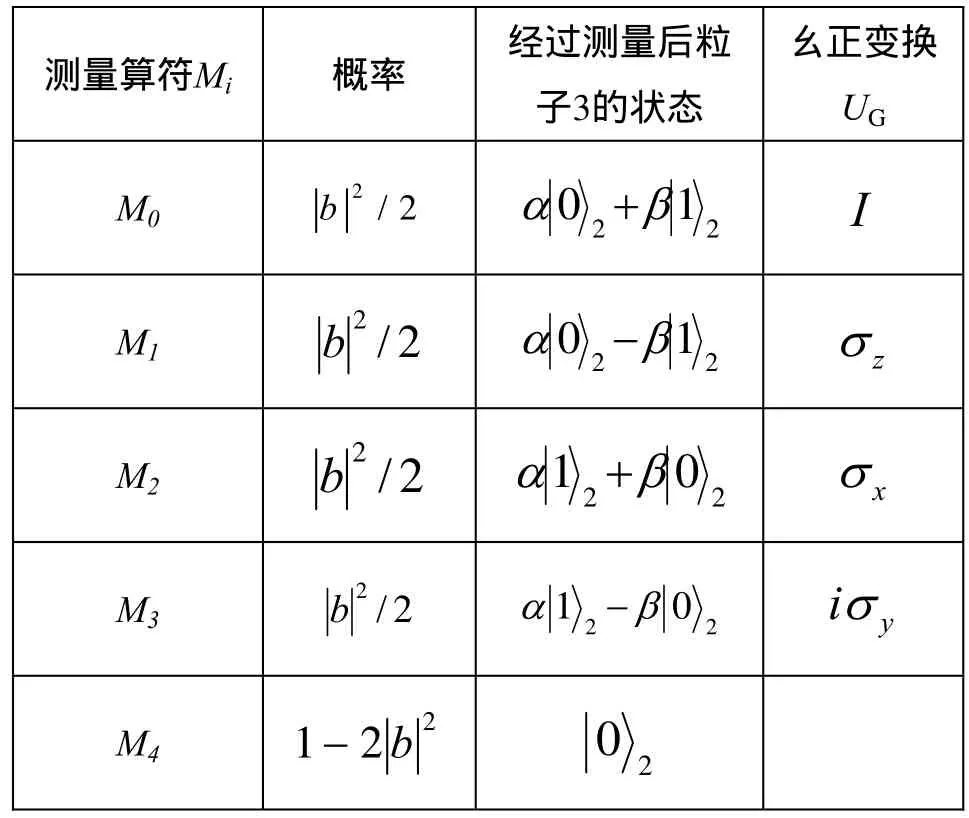
表2 廣義測量的結果和幺正變換UG
3 結論
本文采用推廣測量法,在僅發送者Alice知道部分糾纏GHZ態通道信息的條件下,提出了實現可控概率隱形傳態的方案。其主要過程為
第一步,控制者對他擁有的兩個粒子進行一次Bell基測量,使其它粒子實現糾纏交換。根據控制者的測量結果,發送者對自己的粒子做相應的幺正操作,構造量子通道。
第二步,發送者進行一次本地廣義測量,并通過經典通道告訴接收者。
第三步,接收者根據來自發送者的測量結果,執行適當的幺正變換,就獲得了要傳送的量子態,從而完成了未知態的可控量子隱形傳態。
容易證明,如果可控隱形傳態利用最大糾纏態時,成功的概率是1;如果采用部分糾纏態概率成功為特別是,沒有控制者的協作,就不能構造量子通道,就無法實現量子隱形傳態。
本方案不局限于此文,對其他的糾纏態也可做類似的推廣。
[1] C.H. Bennett, G. Brassard, C. Crepeau, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J]. Phys Rev Lett, 1993, 70 (13):1895-1899.
[2]D. Bouwmeester, J.W. Pan, K. Mattle,et al. Experimental quantum teleportation[J].Nature, 1997, 390, 575-579.
[3]H.Y.Dai,P.X.Chen,C.Z. Li. Probabilistic teleportation of an arbitrary two-particle state by a partially entangled threeparticle GHZ state and W state[J].Optics Communications, 2004,231(1-6): 281-287.
[4]洪智慧,聶義友,黃亦斌,等.基于四粒子團簇態的可控量子隱形傳態[J].量子電子學報,2008, 25(4):458-461.
[5]W.L. Li, C.F. Li, G.C. Guo. Probabilistic teleportation and entanglement matching[J]. Phys. Rev. A, 2000, 61(3): 034-301.
[6]H.Y. Dai, P.X. Chen, C.Z. Li. Probabilistic tele- portation of an arbitrary two-particle state by two partial three-particle entangled W states[J]. Opt. B, 2004, 6(1):106-108.
[7]劉俊昌,李淵華,聶義友.基于糾纏交換和團簇態實現二粒子任意態的可控隱形傳態[J]. 光子學報, 2010, 39 (11): 2078-2081.
[8]李得超,史忠科. 基于混合糾纏態的概率隱形傳態[J].光子學報, 2009, 38(4):983-986.
[9]J.H. Wei,H.Y.Dai,M.Zhang.A new scheme for probabilistic teleportation and its potential applica- tions[J]. Commun. Theor.Phys.,2013,60(6): 651–657.
[10]J.W. Pan,D.Bouwmeester,H.Weinfurter,et al. Experimental entanglement swapping: Entangling photons that never interacted [J]. Phys. Rev. Lett., 1998, 80(18):3891-3894.
[11]A.Karlsson,M.Bourennane.Quantum teleportation using three-particle entanglement[J].Phys. Rev. A, 1998, 58, 4394-4400.
A controlled probabilistic teleportation when only the sender knows partial entangled channel
XIA Li-Xin LI Chao JIA Wen-Tao
(Department of Physics and Technology, Henan University of Science and Technology, Luoyang, 471023, China)
Using the generalization measurement operators, we present a scheme to realize the controlled probabilistic teleportation when only the sender Alice knows all of the information for the partial entangled GHZ state as a quantum channel.
GHZ State; Entanglement Exchange; Generalized Measurement; Controlled Probabilistic Teleportation
O436
A
1673-2219(2014)05-0026-03
2014-03-19
國家自然基金(10674018),湖南省自然基金(06JJ5015),中國博士后基金(20070420379)和河南科技大學人才培養基金(06025)
夏立新(1966-),男,湖南安化人,理學博士,教授,主要從事量子光學、量子計算和量子信息等方向的研究。
(責任編校:劉志壯)

