決策樹在風險管理中的應用分析
張德江
(重慶市建筑科學研究院,重慶 400020)
引言
一個企業在進行決策時,面對的風險紛繁復雜,若決策不當會給企業帶來很大損失。因此,必須對面臨的各種風險進行識別和分析,對各種方案進行比較和選擇,正確決策,以最小風險的投入,獲得可能的最大收益。當管理者面對的未來情況不止一種,而對未來最終可能會出現的結果又無法肯定,但卻知道各種情況在各種自然狀態下發生的概率時,就可采用決策樹這一方法,進行對比分析,以作出最有利的決策。
1 決策樹的原理
決策樹(Decision Tree)又叫決策圖,最早產生于上世紀60年代到70年代末,是直觀運用概率分析的一種圖解法,是一種在已知各種情況發生概率的基礎上,利用風險收益分析,評價項目風險,判斷其可行性的決策分析方法。其本質是通過一系列規則對數據進行分類的過程,是一種逼近離散函數值的方法,是數據挖掘分類算法中最直觀的一種。
2 決策樹的定義
決策樹是一種通過圖示羅列解題的有關步驟以及各步驟發生的條件與結果,從而作出決策的一種方法。該法將各種可行方案,可能出現的自然狀態及其發生概率以及產生的后果(綜合損益期望值)等諸多因素繪在同一張圖上,然后對圖中的各種方案在不同自然狀態下的綜合損益期望值進行計算,再比較各值的大小,最后選出較好方案,因其結構形如樹枝,故稱為決策樹。
3 決策樹的構成
決策樹的構成有五個要素:決策點、方案枝、狀態結點、概率分支和結果結點。
3.1 □——決策結點:是對幾種可能方案分析選擇后選擇的最佳方案。用小方塊□表示。
3.2 ○——狀態結點:代表備選方案的經濟效果 (期望值),通過各狀態節點的經濟效果的對比,按照一定的決策標準就可以選出最佳方案。用小圓圈○表示。
3.3 方案枝:由決策結點引出到狀態結點的若干條細支,每條細支代表一個方案,稱為方案枝。用線段表示。
3.4 概率枝:由狀態節點引出的分支稱為概率枝,每條概率枝代表一種自然狀態。在每條細枝上標明客觀狀態的內容和其出現概率。用線段表示。
3.5 △——結果節點:在概率枝的最末稍標明該方案在該自然狀態下所達到的結果(收益值或損失值)。用小三角形△表示。
4 決策樹的特點
4.1 優點
(1)生成的模式簡單易于理解和實現。
(2)計算量相對來說不是很大。
(3)分類精度高。
(4)能夠直接體現數據的特點,只要通過解釋后都有能力去理解決策樹所表達的意義。
(5)在相對短的時間內能夠對大型數據源做出可行且效果良好的結果。
4.2 缺點
(1)對有時間順序的數據,需要很多預處理的工作。
(2)當類別太多時,錯誤可能就會增加得比較快。
5 決策樹的應用場合
決策樹表達決策問題的方式形象生動,邏輯關系清晰明了,程序嚴謹,定量與定性分析相結合,能將問題各方面的邏輯關系條理化、簡單化,便于研究、分析、修改、補充,方法簡單,易于掌握。在企業管理實踐中,經常會遇到這樣的情景:若干個可行性方案制訂出來了,企業內外部環境,大部分條件是已知的,但還存在一定的不確定因素。每個方案的執行都可能出現幾種結果,各種結果的出現有一定的概率,存在著一定的勝算,也存在著一定的風險。這時,決策的標準只能是期望值。即,各種狀態下的加權平均值。針對上述問題,用決策樹法來解決則不失為一種好的選擇。在企業的投資決策之中,它是隨機決策模型中最常見、最普及的一種決策模式和方法,能有效地控制決策帶來的風險,適用于在比較復雜的情況下進行決策。
決策樹法屬于風險型決策方法,不同于確定型決策方法,二者適用的條件也不同。應用決策樹決策方法必須具備以下條件:
(1)具有期望達到的明確目標。
(2)存在可以選擇的兩個以上的可行備選方案。
(3)存在著決策者無法控制的兩種以上的自然狀態(如氣候變化、市場行情、經濟發展動向等)。
(4)不同行動方案在不同自然狀態下的收益值或損失值(簡稱損益值)可以計算出來。
(5)決策者能估計出不同的自然狀態發生概率。
6 決策樹的應用步驟
6.1 繪制決策圖
(1)首先繪出決策點,即決策樹的始點,用符號□表示。
(2)由決策點開始,自左向右展開,用直線段引出若干方案枝,每條方案枝代表一個可行性方案,在其線段上方標明其方案內容。
(3)在各方案枝末端用符號○表示方案狀態結點。
(4)從各方案狀態結點用直線段引出若干概率分支,每條概率分枝代表一種自然狀態,在其線段上方標明該自然狀態發生的概率P。
(5)在各概率分枝末端標出結果結點,用符號△表示,將該狀態下的損益值q標在△右側。
6.2 分析-比較-決策
(1)由右向左逐步后退進行分析、計算各種狀態下的綜合損益期望值,將其結果標注在○上方。
某方案的綜合損益期望值q=∑ (方案在某種自然狀態下發生的概率×該自然狀態下的損益值)。
(2)比較不同方案的綜合損益期望值,選出合理的決策方案,兩害相權取其輕,兩利相權取其重,最后確定選定的方案,標注在□上方;未被選用的方案則用兩平行短線截斷,稱為“剪枝”。
6.3 對方案的優劣及可靠性進行評價(一般用于兩個方案的情況)

表1 經營安全狀況比較
方法三:計算各方案在為低于轉折概率p的某個概率Pd時(一般可取Pd=(0.8~0.9)p),其綜合損益期望值的變化率Kd,Kd大的方案可靠性較差。
7 案例
例題1:決策樹法在施工管理決策中的應用之一
某建設工程需要特種水泥用于防水工程,又需特種鋼材用于鋼結構工程。但兩種材料的供應都很緊張,受運輸等條件限制,施工時只能保證一種材料得到供應。若水泥供應得到保證,則防水工程將投資30萬元,否則將虧損10萬元。若鋼材供應得到保證,則鋼結構工程投資為50萬元,否則將虧損25萬元。而水泥供應的保證率為0.4,鋼材供應的保證率為0.6。問該優先保障水泥供應或保障鋼材供應?
解:
第一步:繪制決策樹如下。
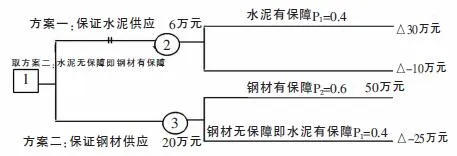
第二步:由右向左逐步后退進行分析、計算各方案的綜合損益期望值q并將結果標在點②、③之上。
點②:q1=30×0.4+(-10)×(1-0.4)=6(萬元)
點③:q2=50×0.6+(-25)×(1-0.6)=20(萬元)
第三步:比較決策。
因為q2>q1,所以決策點取q2=20萬元,即采用保障鋼材供應的方案,將結果標在□上。并用兩平行短線將方案一切斷。
第四步:進一步對方案的優劣及可靠性進行評價。
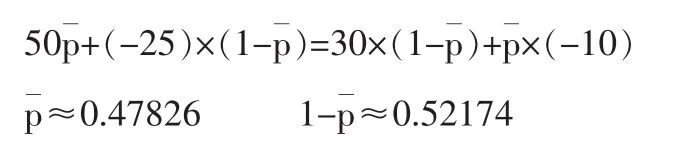
因為P2=0.6 即P2>,所以保障鋼材供應的方案較優。
方法二:計算決策安全率K

此K值較大,查表可知:選擇保障鋼材供應的決策方案,經營較安全。
方法三:比較各方案保證概率低于轉折概率時,其綜合損益期望值變化率Kd
計算各方案在鋼材保證率下降為0.430434時的綜合損益期望值變化率Kd

說明當鋼材供應保證率低于轉折概率時,其綜合損益期望值的變化率比水泥的相應變化率小得多,即鋼材供應保證率的變化對工程的影響不大,所以該方案的可靠性較高,這與前面的分析結果基本一致。
結論:應采用保障鋼材供應的方案。
例題2:決策樹法在施工管理決策中的應用之二
有一項工程,施工管理人員需要決定下月是否開工。如果開工后天氣好,則可為國家創收8萬元;若開工后天氣壞,將給國家造成損失2萬元;不開工則損失2000元。根據過去的統計資料,下月天氣好的概率是0.3,天氣壞的概率是0.7。請做出決策。
解:
第一步:繪制決策樹如下。

第二步:由右向左逐步后退進行分析、計算各方案的綜合損益期望值q并將結果標在點②、③之上。
點②:q1=8.0×0.3+(-0.2)×0.7=2.26(萬元)
點③:q2=(-0.2 ×0.3+(-0.2)×0.7=-0.74(萬元)
第三步:比較決策。
因為q1>q2,所以決策點取q1=2.26萬元,即采用開工的方案,將結果標在□上。并用兩平行短線將方案二切斷。
第四步:進一步對方案的優劣及可靠性進行評價。
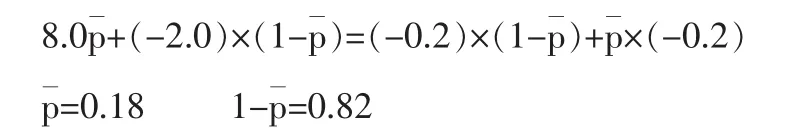
因為P1=0.3 即P1>,所以開工的方案較優。
方法二:計算決策安全率K
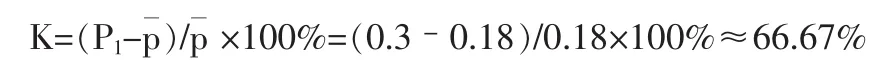
此K值較大,查表可知:選擇開工的決策方案,經營安全。
方法三:比較各方案保證概率低于轉折概率時,其綜合損益期望值變化率Kd
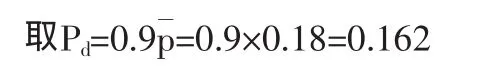
計算各方案在天氣好保證率下降為0.162時的綜合損益期望值變化率Kd
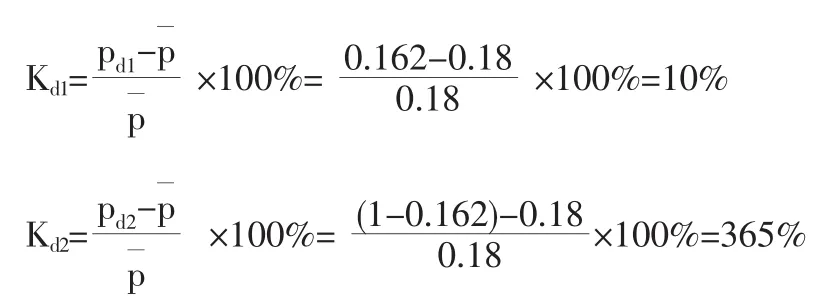
說明當天氣好保證率低于轉折概率時,其綜合損益期望值的變化率比天氣壞的相應變化率小得多,即天氣好保證率的變化對工程的影響不大,所以該方案的可靠性較高,這與前面的分析結果基本一致。
結論:應采用開工的方案。
例題3:決策樹法在投標決策中的應用
某建筑公司打算參加甲、乙兩項工程的投標。因受本單位資源條件限制,只能選擇其中一項工程投標。根據過去類似工程投標的經驗數據,甲工程投高標的中標概率為0.3,投低標的中標概率為0.8,編制該工程投標文件的費用為5萬元;乙工程投高標的中標概率為0.5,投低標的中標概率為0.6,編制該工程投標文件的費用為3萬元。各方案承包的效果、概率、損益值如表2所示。問如何確定投標方案?
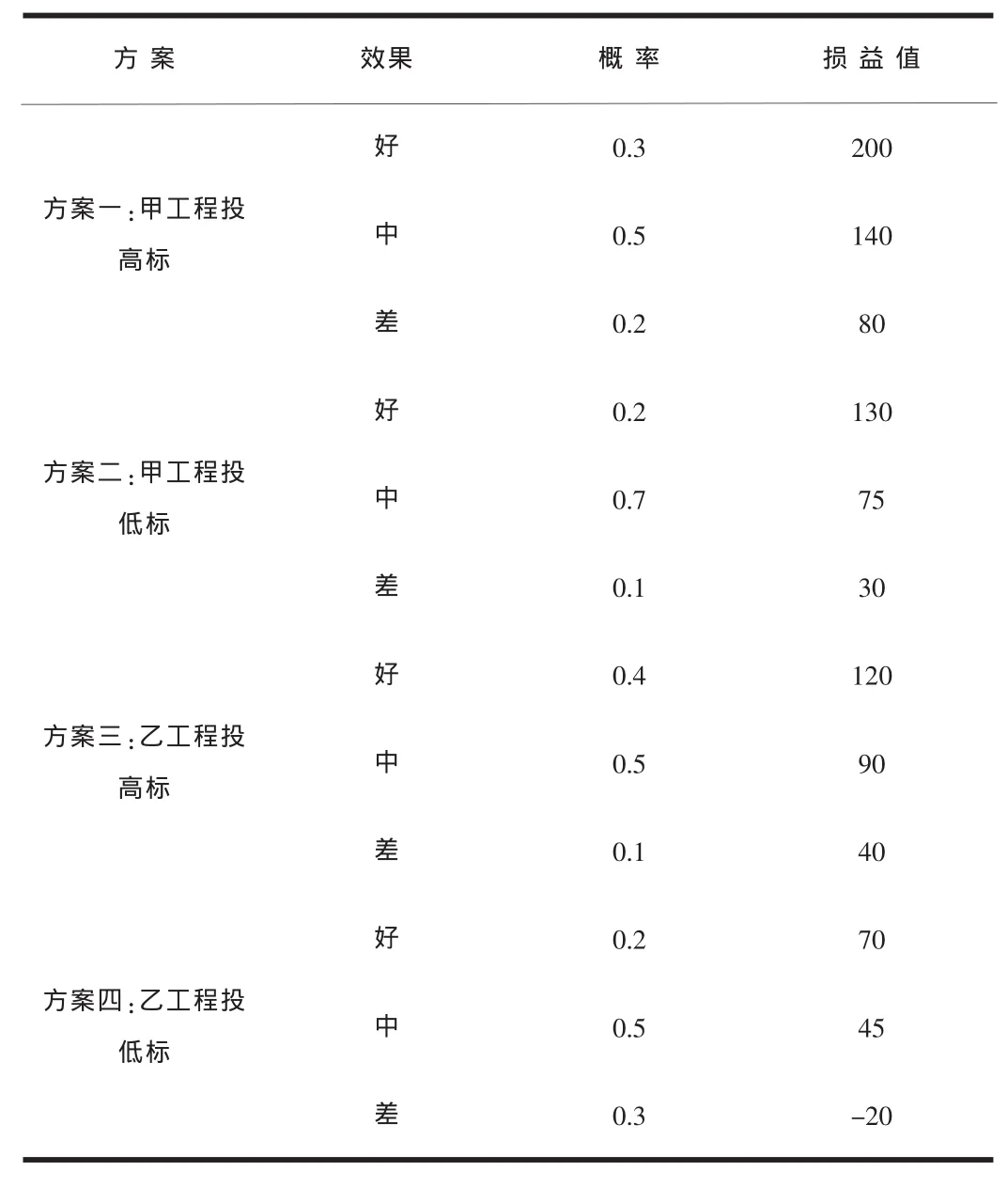
表2 各投標方案的效果、概率、損益值
解:
第一步:繪制決策樹如下。
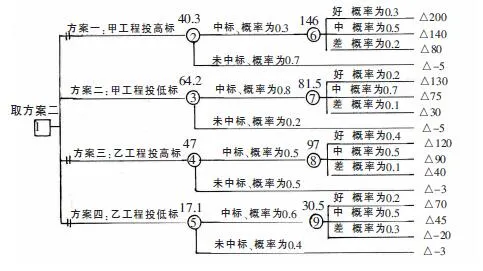
第二步:由右向左逐步后退進行分析、計算各方案的綜合損益期望值q并將結果分別標在點⑥、②、⑦、③、⑧、④、⑨、⑤之上。
點⑥:q6=200×0.3+140 ×0.5+80×0.2=146(萬元)
點②:q2=146×0.3+(-5)×(1-0.3)=40.3(萬元)
點⑦:q7=130×0.2+75×0.7+30×0.1=81.5(萬元)
點③:q3=81.5×0.8+(-5)×(1-0.8)=64.2(萬元)
點⑧:q8=120×0.4+90×0.5+40×0.1=97(萬元)
點④:q4=97×0.5+(-3)×(1-0.5)=47(萬元)
點⑨:q9=70×0.2+45×0.5+(-20)×0.3=30.5(萬元)
點⑤:q5=30.5×0.6+(-3)×(1-0.6)=17.1(萬元)
第三步:比較決策。
比較②、③、④、⑤ 點的綜合損益期望值q,q3=64.2萬元最大,所以決策點取q3=64.2萬元。即采用方案二:甲工程投低標的方案,將結果標在□上。并分別用兩平行短線將其他方案枝切斷。
結論:應采用甲工程投低標的方案。

