鋼束的超欠張拉對PC連續梁橋變形的影響分析

蔡志鋒，寧貴霞，趙生群

(蘭州交通大學土木工程學院，甘肅蘭州730070)

預應力混凝土連續梁橋具有結構受力性能好、變形小、伸縮縫少、行車平穩舒適、養護方便、造型簡潔美觀等優點，且其設計、施工技術成熟，跨越能力大，造價經濟，因此近年來在公路和鐵路工程中被廣泛采用。然而在施工中由于各種原因可能導致預應力鋼束張拉程度有所不同，這樣會造成結構內力分布不均，導致成橋線形不順暢而致行車安全性降低。

影響連續梁橋的撓度有很多因素，如施工過程中移動掛籃、澆筑梁段、張拉預應力筋和體系轉換等主要施工工序。這些因素可改變橋梁結構的受力或變形，對施工中的主梁撓度會有不同程度的影響，成橋后結構自重、橋面鋪裝以及運營活載、收縮徐變等使橋跨結構也會發生變形而產生相應的撓度。

本文結合一座三跨連續梁橋的數值模型，通過調整預應力鋼束的張拉控制應力的方式，探討預應力束的張拉程度對于合龍階段各因素產生撓度的累計值以及成橋后恒載、預應力、徐變、收縮、活載效應產生撓度的影響。

1 工程概況

某公路橋上部結構為三跨(45 m+70 m+45 m)預應力混凝土變截面連續箱梁，采用單箱單室截面，梁高按圓曲線變化，曲線半徑為213.54 m，支點梁高4.5 m，中跨跨中梁高2.0 m。該橋的支點處高跨比為1/15.6，中跨跨中處高跨比為1/35，該橋主梁的總體布置和控制截面如圖1。

2 計算方法和原理

以圖2所示變截面的懸臂施工橋梁為例，文獻［1］中分別得出在懸臂施工狀態、合龍后狀態的梁體撓度的計算公式。

(1)懸臂狀態。

由圖2(a)的原理圖可得到懸臂狀態的梁體端部撓度計算式:

式中:fi為懸臂狀態第i號梁段端部撓度(m);Mi為第i號梁段的彎矩平均值，可近似取該段始末截面彎矩算術平均值，Mi=MT-MO，其中箱梁自重彎矩MO=xi·Gi，預應力彎矩MT=T上·z(kN·m);EiIi為第i段梁段的截面抗彎剛度，可近似地取該段始末截面抗彎剛度之算術平均值。

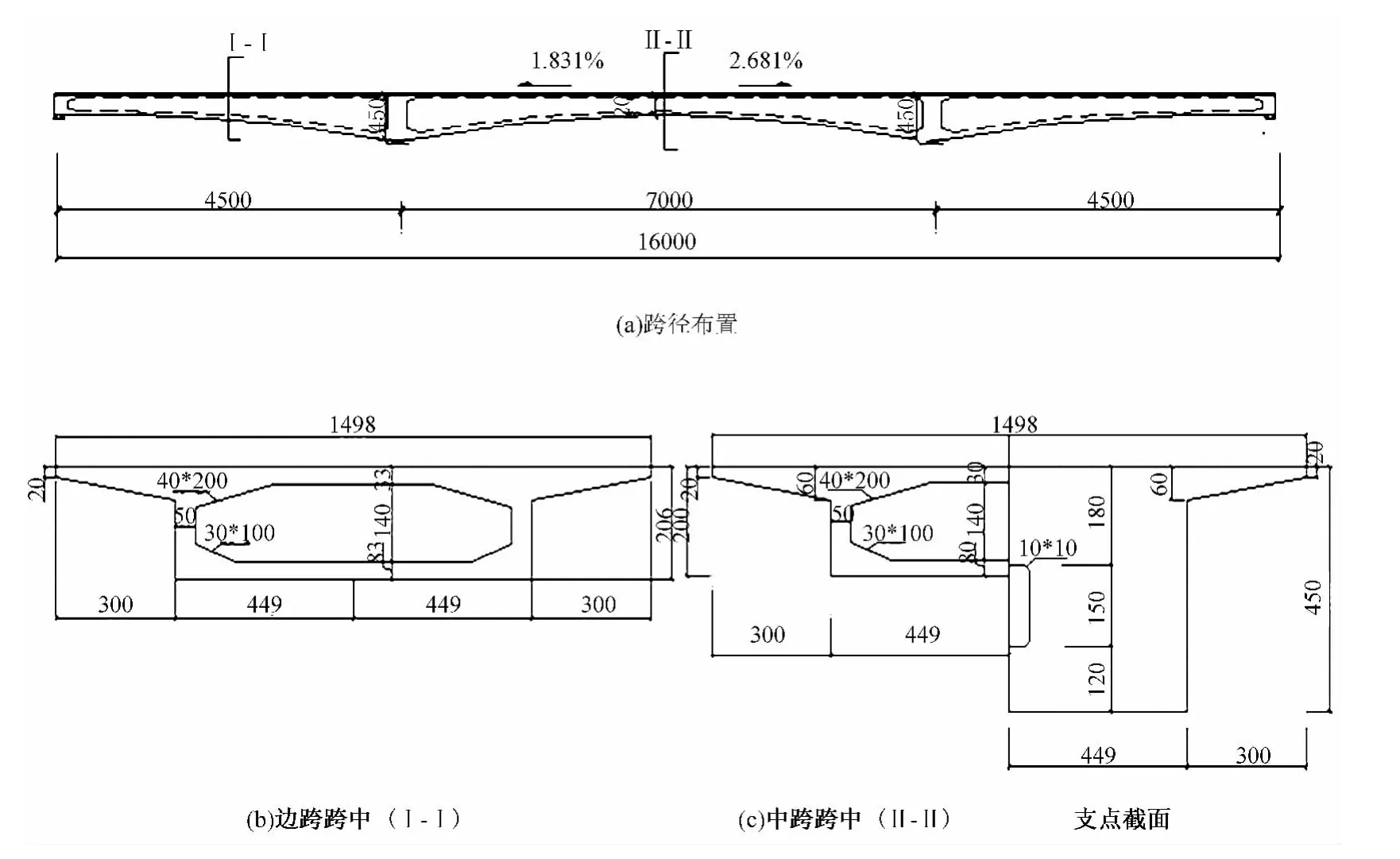
圖1 主梁的跨徑布置及其控制截面(單位:cm)

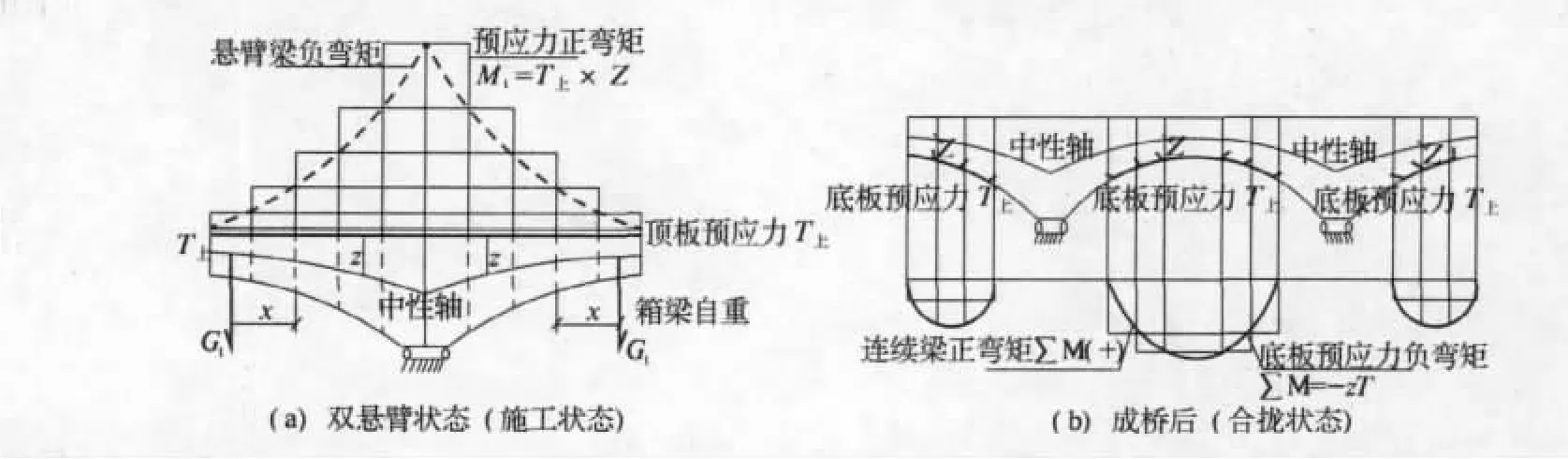
圖2 撓度計算原理圖

(2)成橋狀態。

由圖2(b)的原理圖可得到成橋狀態的跨中撓度計算式:

式中:ft為成橋狀態的跨中撓度(m);Mp為成橋狀態時預應力和恒載對主梁產生彎矩的代數和，Mp=M'T-M'O;其中M'O為連續梁正彎矩，預應力彎矩M'T=T下·z(kN·m)為單位力(P=1)作用在跨中所產生的主梁彎矩(m);EI為成橋后主梁的截面抗彎剛度。

3 分析模型

3.1 模型的建立

(1)幾何模型。

按照圖1的主梁幾何尺寸建立幾何模型，并對梁體內的鋼束進行等效模擬。

在建模時，對預應力鋼束的布置情況按設計圖紙進行定位模擬。在施工中，跨中截面的鋼束布置如圖3，其中在最大懸臂階段僅有頂板束。加載時，把梁體內鋼束的預應力荷載模擬為等效的荷載作用到梁體單元的節點上。

圖3 控制斷面預應力鋼束布置(單位:cm)

(2)有限元模型。

對預應力混凝土箱梁橋分析時，通過MIDAS/Civil結構分析軟件，采用空間梁單元進行懸臂掛籃施工過程的模擬分析，全橋共劃分為59個梁單元，60個節點。為準確模擬梁體截面變化，梁端部采用按線性變化的變截面梁單元，全橋成橋后模型如圖4。

圖4 有限元劃分模型

(3)邊界條件。

在施工階段時，墩梁之間的約束條件采用固結方式;在成橋階段，墩梁之間的約束條件主跨中的一個墩采用固定支座，其余均為活動支座;結構在此過程中實現了由靜定結構向超靜定結構轉化的體系轉換過程。

3.2 計算參數

(1)預加力狀態參數。

對于預應力筋和管道間的摩阻系數以及管道偏差系數，通過在零號塊澆筑后、張拉之前的現場摩阻實驗進行測試，通過實驗分析分別確定為μ=0.17，k=0.001 5來計算預應力損失。預應力鋼束的實際錨下張拉控制應力為1 395 MPa。

(2)荷載及材料參數。

鋼筋混凝土容重取26 kN/m3，二期恒載取80 kN/m。施工中掛籃荷載采用集中力和力矩來加載，其中集中力為-300 kN，力矩為675 kN·m。

混凝土強度采用28 d立方體的抗壓強度，C50混凝土彈性模量取3.45×104MPa。

4 數值模擬分析

對于分析模型按照鋼束超欠張拉的不同程度進行加載，探討對梁體施工及成橋線形的影響。

4.1 分析方案

對于該預應力混凝土連續梁橋，采取調整鋼束張拉控制應力的方法，對于懸臂束和合龍束的控制應力在±30%范圍進行超、欠張拉變化進行加載分析，探討預應力鋼束的張拉程度對于連續梁橋撓度的影響。具體方案如下:

(1)懸臂束以欠、超張拉進行加載，合龍束保持設計控制應力不變;

(2)懸臂束保持設計控制應力不變，合龍束以欠、超張拉進行加載;

(3)對懸臂束、合龍束同時以欠、超張拉進行加載。

4.2 結果分析

計算數據表明:鋼束的不同張拉程度會對合龍階段各因素產生撓度的累計值、成橋后預應力、徐變效應以及總撓度產生一定的影響，而恒載、收縮和活載效應與張拉程度沒有關系，其原因在于預應力鋼束的張拉程度只是改變預應力的加載大小，沒有改變梁體自身的其它結構屬性。

因此本文主要討論分析三種方案對合龍階段、預應力、徐變效應以及總撓度的影響關系。

(1)三種分析方案對撓度影響分析。

在分析中，張拉程度m即為實際張拉控制應力和設計張拉控制應力之差與設計值σcon之比，合龍階段各因素產生撓度的累計值以及成橋后撓度值均以豎直向上為正，向下為負。合龍階段、成橋后預應力、徐變效應下的變形以及總撓度分別用fc、fy、fx、f表示。

將計算的數據按照不同方案進行整理分析討論，得到以下幾方面的結論。

1)懸臂束影響分析。

將懸臂束的不同張拉程度下控制截面在合龍階段、成橋后預應力、徐變效應下的變形以及總撓度的對比情況如圖5所示。

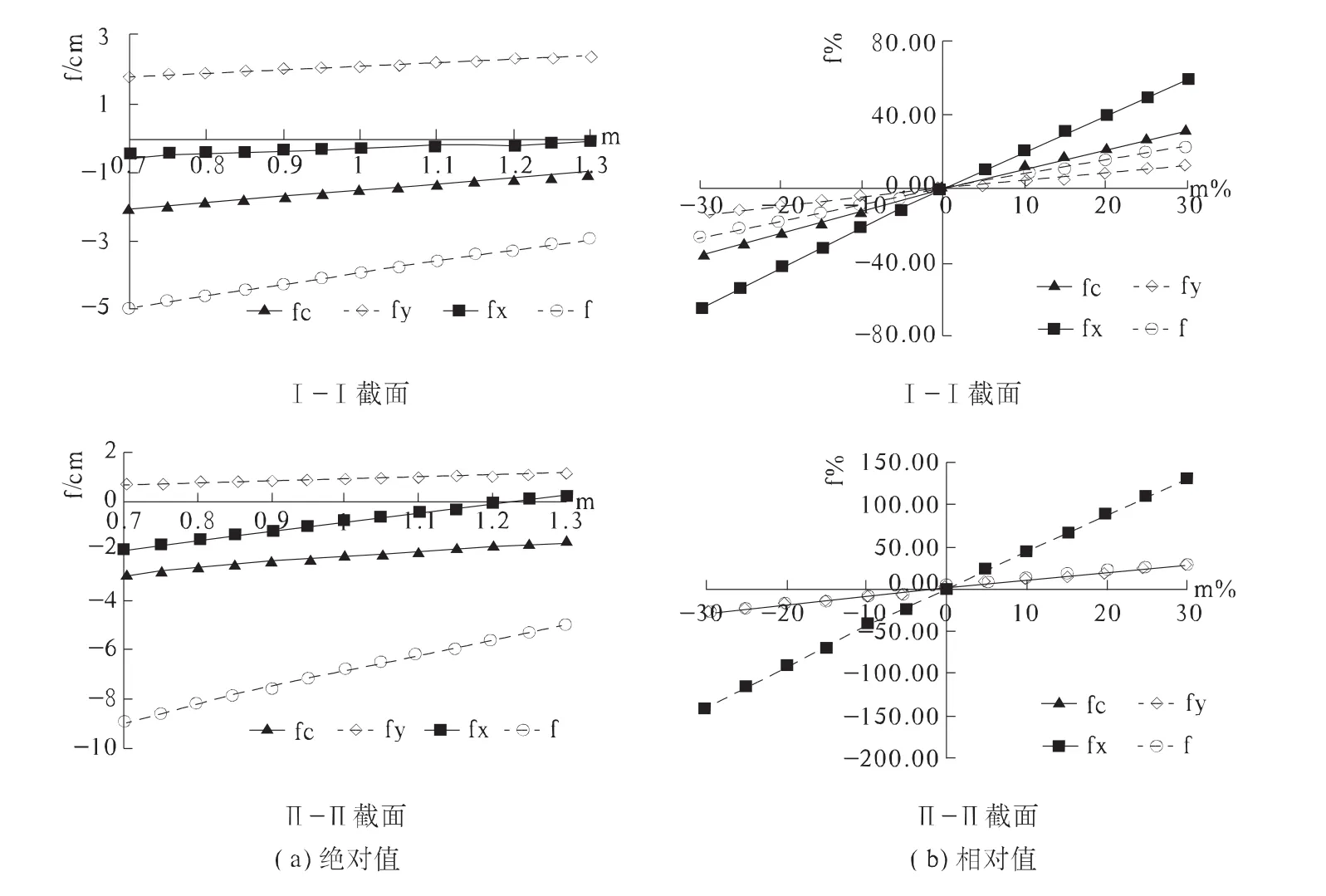
圖5 懸臂束的不同張拉程度下主梁的撓度變化曲線

從圖5中可以看出:

隨著懸臂束張拉控制應力在-30%～30%σcon變化，合龍階段、成橋后預應力、徐變效應變形以及在分析截面處的總撓度均呈線性規律變化。

對于邊跨而言，合龍階段在跨中產生撓度的增幅為-35.75%～31.99%;成橋后預應力效應的增幅為-14.39%～12.69%;徐變效應的增幅為-65.44%～59.40%;即鋼束張拉程度對徐變效應影響最大，對合龍階段的影響次之，對預應力效應的影響最小;各種影響因素綜合作用下對總撓度影響的增幅為-26.51%～23.69%。

對于中跨而言，合龍階段在跨中產生撓度的增幅為-29.59%～25.84%;成橋后預應力效應的增幅為-28.33%～23.32%;徐變效應的增幅為-141.96%～128.66%;即鋼束的張拉程度對徐變效應影響最大，對合龍階段的影響比對預應力效應的影響稍大;各種影響因素綜合作用下對總撓度影響增幅為-30.46%～26.98%。

將邊跨、中跨的跨中撓度對比分析發現:懸臂束的張拉程度對合龍階段變形在邊跨的影響比中跨大，而對成橋后預應力效應、徐變效應以及總撓度在邊跨比中跨影響小。

2)合龍束影響分析。

采用方案一相同的分析方法，對方案二進行計算分析，分析結果如圖6。

圖6 合龍束的不同張拉程度下主梁的撓度變化曲線

從圖6中可以看出:

隨著合龍束張拉控制應力在-30%～30%σcon變化，合龍階段、成橋后預應力、徐變效應變形以及總撓度在邊跨跨中處均呈線性規律變化，但是合龍階段、成橋后預應力中跨跨中處均呈線性減小，徐變效應變形以及總撓度在中跨跨中處呈線性增長趨勢。

對于邊跨而言，合龍階段在跨中產生的撓度增幅為-30.72%～28.30%;成橋后預應力效應的增幅為-14.10%～12.97%;徐變效應的增幅為-115.44%～106.04%;即鋼束的張拉程度對徐變效應的撓度影響最大，對合龍階段的影響次之，對預應力效應的影響最小;各種影響因素綜合作用下對總撓度影響的增幅為-28.26%～26.00%。

對于中跨而言，合龍階段在跨中產生的撓度增幅為-1.02%～0.88%;成橋后預應力效應的增幅為-6.14%～5.01%;徐變效應的增幅為-22.73%～19.95%;即鋼束的張拉程度對徐變效應在中跨的撓度影響最大，對合龍階段、預應力效應的均產生減小的影響，且對預應力效應比合龍階段的影響大;各種影響因素綜合對總撓度影響的增幅為-1.80%～1.28%。

將邊跨、中跨的跨中撓度對比分析發現:合龍束的張拉程度對合龍階段、成橋后預應力效應、徐變效應變形以及總撓度在邊跨均比中跨影響大。

3)懸臂束、合龍束對比分析。

由前面討論得知:恒載、活載、收縮效應的變形與鋼束張拉程度沒有關系，所以在這里也主要對比分析三種方案下合龍階段、預應力、徐變效應以及總撓度的相對關系如圖7。

通過圖7可以看出:

方案一、方案二的相對撓度增幅的代數疊加結果和方案三的相對撓度值相等。以影響幅度最大的徐變效應為例:其在方案一中I-I處撓度的增幅為-65.44%～59.40%，方案二中為-115.44%～106.04%，方案三中為-180.87%～165.44%，方案一和方案二的代數相加結果即為方案三。因而方案三的影響幅度比其它兩種方案均要大。

隨著鋼束張拉控制應力在-30%～30%σcon變化，對三種分析方案、兩個控制截面綜合對比發現:合龍束只是對邊跨跨中處的徐變效應變形影響幅度比懸臂束的大，其它所分析因素的變形分別在兩個控制截面處的變化幅度均為懸臂束比合龍束的影響大。

(2)撓跨比影響分析。

通過計算得出該橋在三種方案下的撓跨比與張拉程度的關系如圖8。

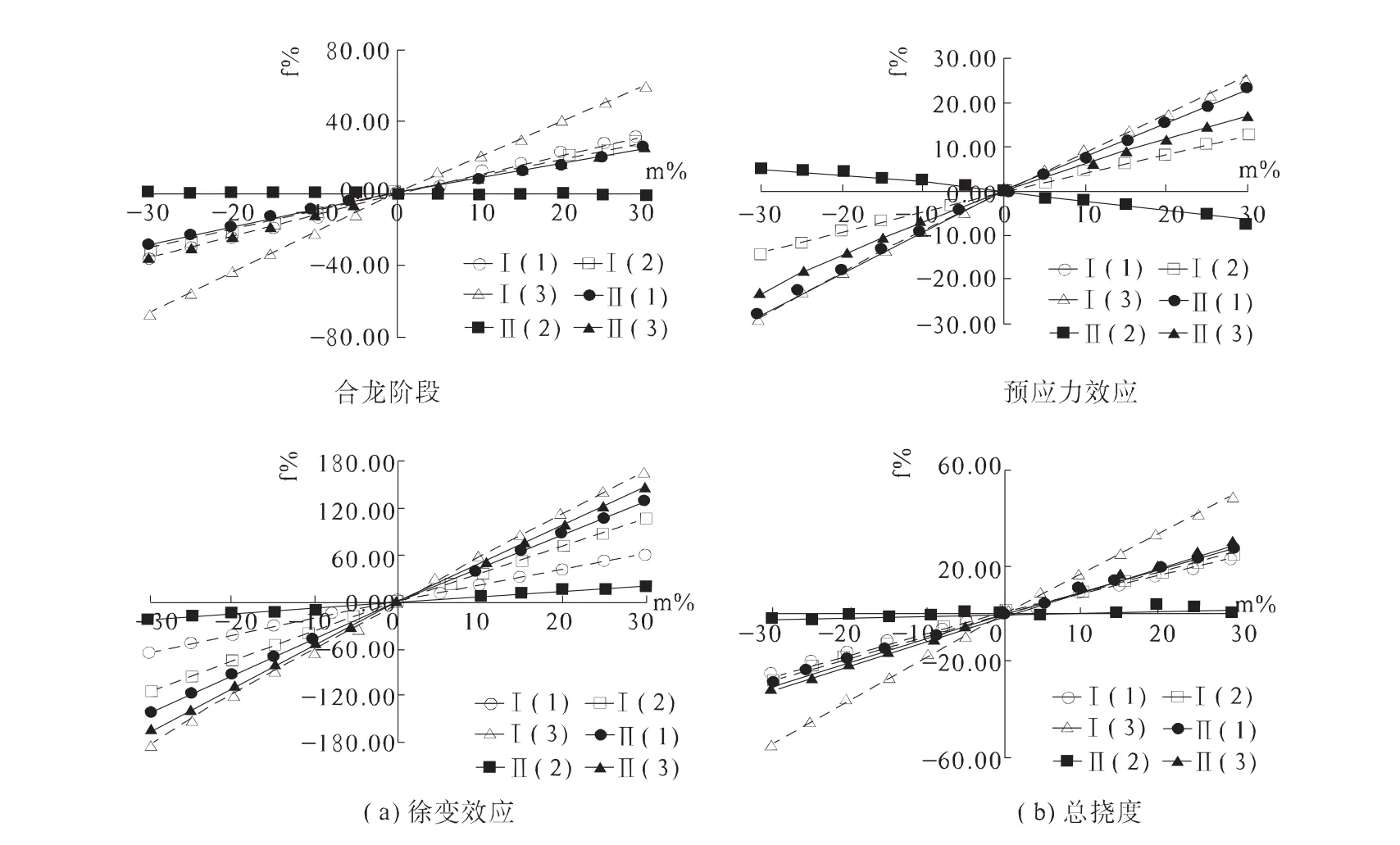
圖7 三種方案主梁相對撓度變化曲線

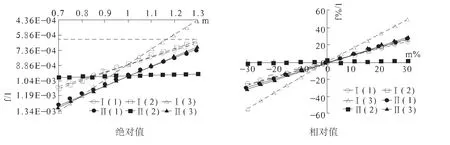
圖8 三種方案的撓跨比變化曲線

通過圖8可以看出，隨著鋼束張拉控制應力在-30%～30%σcon變化，三種方案在控制截面處的撓跨比均呈線性規律變化。方案三對控制截面處撓跨比的影響最大，方案一對中跨比邊跨的影響大，方案二、三對邊跨比中跨的影響大。且當對懸臂束、合龍束同時超張拉20%時，邊跨跨中處的撓跨比f/l=1/1 740=5.75×10-4≤6.25×10-4=1/1 600，結合規范對預拱度的設計原則，其對預拱度會有一定的影響。

《公路橋規》［2］中指出:當由結構自重和靜活載產生的撓度不超過l/1 600時，可不設預拱度;當不符合上述規定時，應設預拱度，且其值應按結構自重和1/2可變荷載頻遇值計算的長期撓度值之和采用。由規范本例中當主梁撓跨比f/l≤1/1 600=6.25×10-4時，可不設置預拱度;當撓跨比f/l≥1/1 600=6.25×10-4時，應當按規定設置預拱度。因此在施工中應該合理控制預應力的張拉程度，以保證撓跨比滿足施工中所需設計預拱度的要求。

5 結論

通過調整鋼束張拉控制應力的方式，利用有限元軟件進行數值模擬，對于超、欠張拉對各種因素影響下的主梁撓度、撓跨比進行分析，結果表明:

(1)張拉程度對合龍階段、預應力效應、徐變效應產生的主梁撓度有影響，且以徐變效應的影響最顯著;恒載、收縮、活載效應引起主梁的撓度值與張拉程度沒有關系;隨著鋼束張拉程度的變化，在各種影響因素下跨中的總撓度隨之呈線性增長規律，且欠張拉的影響幅度比超張拉稍大。

(2)張拉程度不同時，合龍束只是對邊跨的徐變效應影響顯著，其它所分析因素變形均受懸臂束的影響比較大，為控制主梁施工階段以及成橋后線形，應對懸臂束和邊跨的合龍束選擇合適的張拉控制應力。

(3)鋼束的張拉程度對主梁撓跨比會產生影響，進而會影響預拱度的值。當對懸臂束、合龍束同時超張拉20%時，邊跨跨中的撓跨比超過預拱度設計原則的臨界值。

本文在討論中只涉及了鋼束超欠張拉不同程度的影響時的三種張拉方案，對于同一截面上的不同位置鋼束的超欠張拉同時存在的情況還需進一步探討。

［1］郭圣棟，任亮.梁橋恒載跨中撓度允許值［f_t］確定［J］.預應力技術，2012(2):21-29.

［2］JTG D62—2004.公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］.

［3］雷俊卿.橋梁懸臂施工與設計［M］.北京:人民交通出版社，2000.

［4］宋郁民，劉源，周世軍.預應力混凝土橋梁懸臂施工中徐變撓度的計算［J］.蘭州交通大學學報，2008，27(4):25-27.

［5］饒瑞.部分預應力混凝土連續梁橋梁端縮短問題的研究［D］.廣州:華南理工大學，2005.

［6］孫學先，張慧，張兆寧.位移反分析在梁橋懸臂施工線形控制計算中應用［J］.蘭州交通大學學報，2006，12(25):49-52.

［7］程亮，周偉.懸臂施工預應力混凝土連續梁橋中跨合龍段底板豎向應力探討［J］.現代交通技術，2010(5):41-50.

［8］宋麗加.大跨度預應力混凝土連續梁懸臂施工控制研究［D］.成都:西南交通大學，2004.

［9］吳鴻慶，任俠.結構有限元［M］.北京，中國鐵道出版社，2000.