不同特性介質(zhì)對邊壁流效應(yīng)的影響

苑藝琳， 王福剛， 靖 晶， 高振凱

(吉林大學(xué) 環(huán)境與資源學(xué)院, 地下能源與廢物處置研究所， 吉林 長春 130021)

0 引 言

邊壁流效應(yīng)是指一定的水力條件下，保持有某種物理屬性和化學(xué)成分的流體，在某種介質(zhì)中滲透時，受邊壁粗糙度、幾何特征以及水理性質(zhì)的影響[1]，而發(fā)生在邊界附近的不均勻水流滲透和溶質(zhì)運移過程[2-3]。在室內(nèi)水流或溶質(zhì)運移實驗過程中，該效應(yīng)一旦發(fā)生，對地下水滲流和溶質(zhì)的時空分布將產(chǎn)生影響，干擾實驗結(jié)果。

邊壁流效應(yīng)在多個領(lǐng)域受到科學(xué)工作者的注意，但孔隙介質(zhì)地下水滲流和溶質(zhì)(或污染質(zhì))運移實驗中，邊壁流效應(yīng)還沒有引起研究人員的足夠重視，目前對邊壁流效應(yīng)的研究仍處于定性研究階段，并且缺乏系統(tǒng)性和全面性。

本文以室內(nèi)物理實驗獲取的第一手?jǐn)?shù)據(jù)為基礎(chǔ)，以現(xiàn)代計算機技術(shù)、實驗數(shù)據(jù)多種數(shù)學(xué)分析方法為手段[4]，結(jié)合并吸取現(xiàn)代水力學(xué)中邊界層理論在實際應(yīng)用研究中的經(jīng)驗和成果[5]，從與邊壁流效應(yīng)有成生聯(lián)系的實驗介質(zhì)特征(介質(zhì)屬性特征)角度出發(fā)，研究邊壁流效應(yīng)發(fā)展過程和影響因素。通過實驗室試驗，研究不同介質(zhì)特征下，邊壁流效應(yīng)影響區(qū)域與滲流核心區(qū)的水流質(zhì)量交換和流速差異所引起的滲流場、濃度場在縱向、橫向的二維空間上的演化過程[4]。

1 實驗設(shè)計

1.1 試驗裝置

本實驗裝置的原理與達(dá)西滲流實驗[4-6]相似，滲流速度的調(diào)節(jié)通過控制進出水端水頭來實現(xiàn)，實驗裝置圖1所示。為了能穩(wěn)定水頭供水，進水口采用水泵供水，排水出水口采用穩(wěn)定溢流箱[7-8]，在滲流槽內(nèi)均勻布設(shè)18個觀測孔，采用自主研發(fā)的多功能電導(dǎo)率在線檢測儀進行實時監(jiān)測。

1.2 土樣選取

本實驗選用了3種砂土，均取自松花江河底砂，將砂土篩分3次，篩分成細(xì)砂、中砂和粗砂，每次實驗結(jié)束將砂土倒出進行沖洗，曬干后并重新裝樣[9-10]。

實驗采用60 cm×30 cm的滲流槽，在滲流槽內(nèi)裝填高度為30 cm的砂土，因砂土粒徑不同，所以密度也不一樣。因此，參考經(jīng)驗容重，依據(jù)野外自然條件，3種砂土密度分別為：細(xì)砂1.5 cm3/g，中砂1.6 cm3/g，粗砂1.8 cm3/g,按計算值裝填實驗槽，每次裝填1 cm的高度，并記錄下所用砂的質(zhì)量，裝砂密度不均勻會造成實驗偏差，如砂槽出現(xiàn)氣泡或裂隙、密度不均，則需要倒出重裝，保證槽內(nèi)樣品均勻，以滿足實驗要求。

經(jīng)過多次實驗，發(fā)現(xiàn)最適用于本實驗的示蹤劑是NaCl[11]，并通過自主研發(fā)的電導(dǎo)值在線監(jiān)測儀在線監(jiān)測電導(dǎo)率，使實驗中的測量精度得到了很大的提高，實驗數(shù)據(jù)準(zhǔn)確、真實、清晰地把握到在實驗介質(zhì)不同的情況下邊壁滲流速度與非邊界區(qū)域的差異。

2 實驗結(jié)果及分析

2.1 參數(shù)計算

(1) 孔隙度。首先對粗砂、中砂、細(xì)砂的孔隙度進行計算，記錄向槽內(nèi)裝砂的體積V以及砂體飽水時所注入水的體積Vn，如表1所示。通過計算得到粗砂、中砂、細(xì)砂孔隙度n分別為0.300 13，0.237 01，0.414 11。

表1 不同試驗介質(zhì)NaCl初始濃度

(2) 滲透系數(shù)求解。在水頭差為4 cm條件下，對3種實驗介質(zhì)滲透系數(shù)進行計算。根據(jù)達(dá)西定律，通過計算得到結(jié)果如表2所示。

表2 3種不同介質(zhì)的實驗參數(shù)表

2.2 速度求解

為了探明邊壁流效應(yīng)對地下水滲流速度的影響，需將NaCl濃度轉(zhuǎn)化成水流速度。經(jīng)分析與推算，得到對流彌散方程[4，12-13]

(1)

式中：c為某一觀測孔某一時刻NaCl濃度值；x為觀測孔橫坐標(biāo)；t為某時刻時間；m為單位橫截面積上瞬時注入示蹤劑的質(zhì)量；ω表示橫截面積；n為試驗介質(zhì)的孔隙度；DL為彌散系數(shù)；u為滲流速度。

對于任意2個觀測孔(如圖1中1-1、2-1觀測孔)在其濃度達(dá)到最大值時其對流彌散方程的導(dǎo)數(shù)為0，即c′=0,對c求導(dǎo)得：

(2)

整理得到：

代入2個觀測點的x值和達(dá)到峰值的時間t值,得到關(guān)于u、DL的二元二次方程組，即可解得這2個觀測孔之間的滲流速度，例如，代入中砂H=4 cm時數(shù)據(jù)，x1=22,x2=37，t1=130,t2=220,得到：

解得：u= 0.002 778，DL=0.000 937 257。

2.3 濃度曲線

由于實驗室條件限定，NaCl濃度無法實時監(jiān)測，在實驗中示蹤劑NaCl的濃度是通過測量NaCl的電導(dǎo)值而間接測得的。為了提高實驗的測量精度以及數(shù)據(jù)的準(zhǔn)確性，本實驗采用電導(dǎo)值在線監(jiān)測儀，通過布置的觀測孔對NaCl的電導(dǎo)值進行測量，進而將電導(dǎo)值轉(zhuǎn)換成濃度值[14-15]。為了得到電導(dǎo)率與濃度轉(zhuǎn)化公式，在本實驗NaCl濃度范圍內(nèi)取7組不同濃度進行實驗，并測量它們的電導(dǎo)率值。將NaCl電導(dǎo)率作為橫軸，NaCl濃度作為縱軸，得到NaCl濃度與電導(dǎo)率的相關(guān)直線，求得該直線相關(guān)系數(shù)R2=0.996，非常接近1，說明通過該直線求得的NaCl電導(dǎo)率與濃度轉(zhuǎn)化公式正確，且可以使用[16]。該公式為：c=0.000 04S±0.003,其中，c為NaCl濃度;S為NaCl電導(dǎo)率;0.003為相對誤差。

(1) 粗砂。在水頭差4 cm條件下，將記錄的電導(dǎo)值轉(zhuǎn)化為濃度并繪制濃度曲線，通過曲線發(fā)現(xiàn)滲流槽邊壁兩側(cè)NaCl濃度峰值出現(xiàn)時間早于中部NaCl濃度峰值出現(xiàn)時間。對第2列和第4列觀測孔濃度達(dá)到峰值的時間比較發(fā)現(xiàn)：第2列中間孔相對兩側(cè)孔峰值出現(xiàn)的時間上滯后5 min(占總運移時間的6.31%)，第4列中間孔與兩側(cè)孔的滯后8 min(11.57%)，即溶質(zhì)從第2列運移到第4列的過程中，兩側(cè)溶質(zhì)要優(yōu)先中間到達(dá)第4列。

圖2為t=15 min時的濃度等值線圖，從圖中可以看出，滲流槽邊壁NaCl濃度較中間要小。清楚地看到邊壁流效應(yīng)是存在的，而且對滲流過程影響很大。

圖2 t為15 min的濃度等值線圖

(2) 中砂。在水頭差4 cm條件下，由于水流實際流速中等，使用與粗砂相同的方法計算NaCl濃度值，并繪制濃度曲線和sufer圖。實驗結(jié)果與粗砂相似，即滲流槽邊壁兩側(cè)NaCl濃度峰值出現(xiàn)時間早于中部NaCl濃度峰值出現(xiàn)時間。

對第2列和第4列觀測孔濃度達(dá)到峰值的時間比較發(fā)現(xiàn)：第2列中間孔相對于兩側(cè)孔的滯后時間為40 min(占總運移時間的6.00%)，第4列中間孔與兩側(cè)孔的滯后時間為90 min(13.40%)。圖3為t=280 min時的濃度等值線圖。從圖中可以看出,滲流槽中部示蹤劑運移緩慢，發(fā)生堆積現(xiàn)象，而邊壁兩側(cè)水流對NaCl運移則很快，更加清晰地反映出由于邊壁效應(yīng)的影響，滲流槽邊壁滲流速度與中部速度有很大差異。

圖3 t為280 min的濃度等值線圖

(3) 細(xì)砂。在水頭差4 cm條件下，水流實際流速較小，通過與粗砂、中砂實驗相同的方法，記錄NaCl電導(dǎo)率并計算NaCl濃度值。實驗結(jié)果與中砂、粗砂相似，即滲流槽邊壁兩側(cè)NaCl濃度峰值出現(xiàn)時間早于中部NaCl濃度峰值出現(xiàn)時間。

對第2列和第4列觀測孔濃度達(dá)到峰值的時間比較發(fā)現(xiàn)：第2列中間孔相對于兩側(cè)孔的滯后時間為155 min(占總運移時間的5.17%)，第4列中間孔與兩側(cè)孔的滯后時間為362 min(12.08%)。繪制濃度等值線圖(surfer圖)，由圖反映的現(xiàn)象與中砂基本一致。圖4為t=2 800 min時濃度等值線圖，圖中直觀地驗證了邊壁流效應(yīng)的存在性。

圖4 t為2 800 min的濃度等值線圖

2.4 速度描述

按照式(1)、(2)計算速度值，對于每一行觀測孔來說，有3或4個觀測孔，為保證計算的準(zhǔn)確性，任意2個觀測孔都要計算其速度值，再取平均值，作為此行觀測孔的滲流速度。不同種介質(zhì)中每行平均滲流速度如表3所示。

表3 3種砂中滲流速度每行平均速度表 cm/s

這樣就可求得滲流槽中部水流速度相對于邊壁兩側(cè)水流速度的滯后率。例如，對于粗砂而言，第1行速度為0.022 966，第5行速度為0.030 450，第3行速度為0.019 577。計算如下：

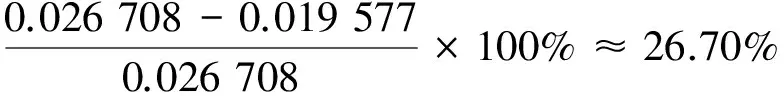
中砂、細(xì)砂中的滯后率計算方法與粗砂相同，滯后率計算結(jié)果為：粗砂26.70%，中砂14.72%，細(xì)砂43.72%。

比較滲流速度的滯后率，當(dāng)水頭差4 cm，實驗介質(zhì)不同時，滲流槽中部與邊壁滲流速度滯后率為：細(xì)砂>粗砂>中砂。

3 結(jié) 語

通過對水力梯度為4 cm的不同實驗介質(zhì)滲流實驗的研究，在濃度監(jiān)測方面，發(fā)現(xiàn)滲流槽中部NaCl濃度總是小于邊壁兩側(cè)濃度。由此在對滲流速度計算分析后，表明在水力梯度為4 cm的地下水滲流實驗中，邊壁兩側(cè)水流速度大于中部。同時，針對每組砂進行水力梯度分別為2、8、12 cm的若干組實驗，也得到了相似的結(jié)果。

本次滲流實驗驗證了地下水滲流場中邊壁流效應(yīng)的存在，由于邊壁流效應(yīng)的存在，對滲流場邊壁附近的滲透系數(shù)起到了增大的作用，對滲透流速起到了增益作用。因此，在水文地質(zhì)實驗中(如：地下水流速、流向測定實驗，彌散實驗，溶質(zhì)或污染質(zhì)運移實驗等)，觀測孔的布設(shè)位置以及采樣點的分布都要充分考慮邊壁效應(yīng)不可忽略的影響。

本文僅針對實驗介質(zhì)，定性地分析了不同實驗介質(zhì)邊壁流效應(yīng)之間的關(guān)系。對于兩者之間定量關(guān)系，以及邊界粗糙程度和水理特性對其影響程度則還需要進一步的實驗。

[1] Boutt David F,Grasselli Giovanni, Fredrich Joanne T,etal.Trapping Zones : The effect of fracture roughness on the directional anisotropy of fluid flow and colloid transport in a singlefracture[J]. Geophys Res Lett, 2006, 33 (21) :L21402.

[2] 王 巖. 黃河口潮間帶沉積物水及溶質(zhì)優(yōu)先遷移的試驗研究[D].青島:中國海洋大學(xué)，2010.

[3] Allaire Suzanne E, Roulier Stéphanie, Cessna Allan J.Quantifying preferential flow in soils: A review of different techniques[J]. Journal of Hydrology, 2009,378(2):179-204.

[4] 薛禹群,朱學(xué)愚,吳吉春,等.地下水動力學(xué)[M].2版. 北京:地質(zhì)出版社，1997:3-66.

[5] Hincapié Ingrid, Germann Peter F.Impact of initial and boundary conditions on preferential flow[J]. Journal of Contaminant Hydrology, 2009, 104(4):67-73.

[6] 劉 凱,文 章,梁 杏,等.一維低滲透介質(zhì)非達(dá)西滲流實驗[J].水動力學(xué)研究與進展(A輯),2013,28(1):81-86.

Liu K, Wen Z，Liang X,etal. One dimensional low permeable medium non-darcy seepage experiment[J]. Chinese Journal of Hydrodynamics, 2013,28(1):81-86.

[7] 王錦國,周志芳.裂隙介質(zhì)水流、溶質(zhì)運移試驗裝置[P].中華人民共和國知識產(chǎn)權(quán)局專利.公告號:CN2699314Y,2005.

[8] 喬云峰.黃土中水鹽運動實驗研究[D].西安：西安理工大學(xué),2001.

[9] 付宏淵，嚴(yán)志偉，李 海. 土柱溶質(zhì)運移試驗的理論驗證及影響因素敏感性分析[J]. 長沙理工大學(xué)學(xué)報,2011,8(4):1-5.

Fu H Y, Yan Z W, Li H. Soil column test solute transport theory and influence factors sensitivity analysis[J]. Journal of Changsha University of Science & Technology, 2011,8(4):1-5.

[10] 賀玉龍，陶玉敬，楊立中.不同節(jié)理粗糙度系數(shù)單裂隙滲流特性試驗研究[J].巖石力學(xué)與工程學(xué)報,2010,29(Sup. 1):3235-3240.

He Y L, Chen Y J, Yang L Z. Different joint roughness coefficient single fracture seepage experimental study[J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(S1):3235-3240.

[11] 李瀟瀚. 基于試驗及模型的凍融過程中水鹽運移規(guī)律研究[D].長春:吉林大學(xué),2013.

[12] 王秉忱,楊天行.地下水污染地下水水質(zhì)模擬方法[M]. 北京:北京師范學(xué)院出版社,1985:12-43.

[13] 黃 琨. 孔隙介質(zhì)滲流基本方程的探索[D].武漢:中國地質(zhì)大學(xué),2012.

[14] 魏新平, 王文焰,王全九,等.溶質(zhì)運移理論的研究現(xiàn)狀和發(fā)展趨勢[J].灌溉排水，1998,17(4):58-63.

Wei X P, Wang W Y, Wang Q J，etal. Study tendency of soil solute transport as affected by irrigation[J]. Journal of Irrigation and Drainage，1998,17(4):58-63.

[15] 蔡金龍,周志芳.粗糙裂隙滲流研究綜述[J].勘察科學(xué)技術(shù),2009(4):18-23.

Cai J L, Zhou Z F. Review of seepage research in rough fracture[J]. Site Investigation Science and Technology,2009(4):18-23.

[16] 速寶玉,詹美禮,趙 堅. 仿天然巖體裂隙滲流的實驗研究[J].巖土工程學(xué)報,1995,17 (5) :19-24.

Su B Y, Zhan M L, Zhao J. Study on fracture seepage in the imitative nature rock[J]. Chinese Journal of Geotechnical Engineering,1995,(17):19-24.