基于LQR方法的扭轉振動裝置控制器設計

王佳偉， 楊亞非， 錢玉恒

(哈爾濱工業大學 飛行器控制實驗教學中心，黑龍江 哈爾濱 150001)

0 引 言

扭轉振動簡稱扭振，是一種常見的機械振動物理現象，當彈性體繞其縱軸發生扭轉變形時，就會產生扭轉振動。扭振大多見于電力系統的汽輪發電機組[1-4]、汽車發動機的曲軸系[5-8]、軋鋼機的傳動機組[9-11]，以及石化行業的煙機等應用場合。

Model205a型扭轉振動裝置是由世界知名的教學設備生產企業美國ECP公司生產制造的，已經在世界上500所大學中推廣應用，其功能和性能都明顯優于國內單位使用或設計的扭振實驗臺[12-14]。該裝置可以模擬單自由度、雙自由度和三自由度系統的扭轉振動特性，分析激勵頻率對系統固有頻率的影響，即分析扭振裝置的頻率響應。該裝置的另外主要功能在于，它是一個數字控制的閉環控制系統，機械部分是一個真實的控制對象，控制器則通過計算機來進行設計，整體相當于一個半實物的仿真平臺，可以對其進行各種控制器的設計和仿真驗證。本文將其機械部分配置成四階的雙自由度的被控對象，通過受力分析推導其等價的數學模型，然后將為其設計一種LQR控制器，最后將經過實驗仿真來驗證控制器的作用效果。

1 裝置簡介

實驗裝置如圖1所示。

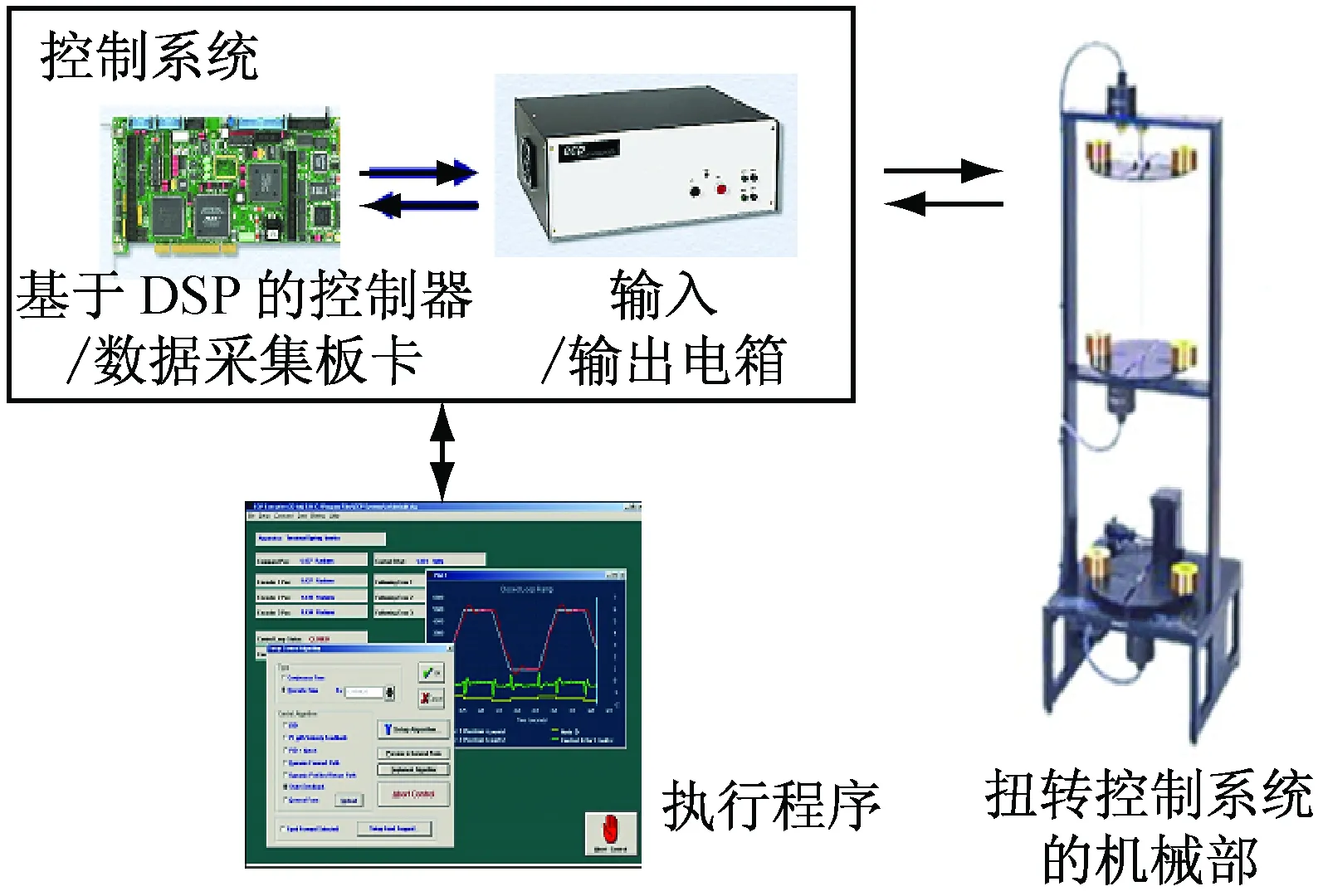
圖1 扭轉振動裝置組成

(1) 扭轉振動裝置的機械部。如圖2所示，扭轉振動裝置由扭轉機械部分、執行器和傳感器構成。扭轉機械部分是由底座、框架、扭轉軸、圓盤、慣量砝碼等組件構成；執行器采用了無刷直流伺服電機；傳感器選用了高分辨率的編碼器。機械部分的彈性軸垂直懸掛在抗摩擦球形軸承上，用來連接3個圓盤。伺服電機通過剛性皮帶(僅存在微小拉伸形變)來驅動底層圓盤和彈性軸，滑輪系統的減速比為3∶1，每個圓盤都配有一個編碼器來測量圓盤的位置。

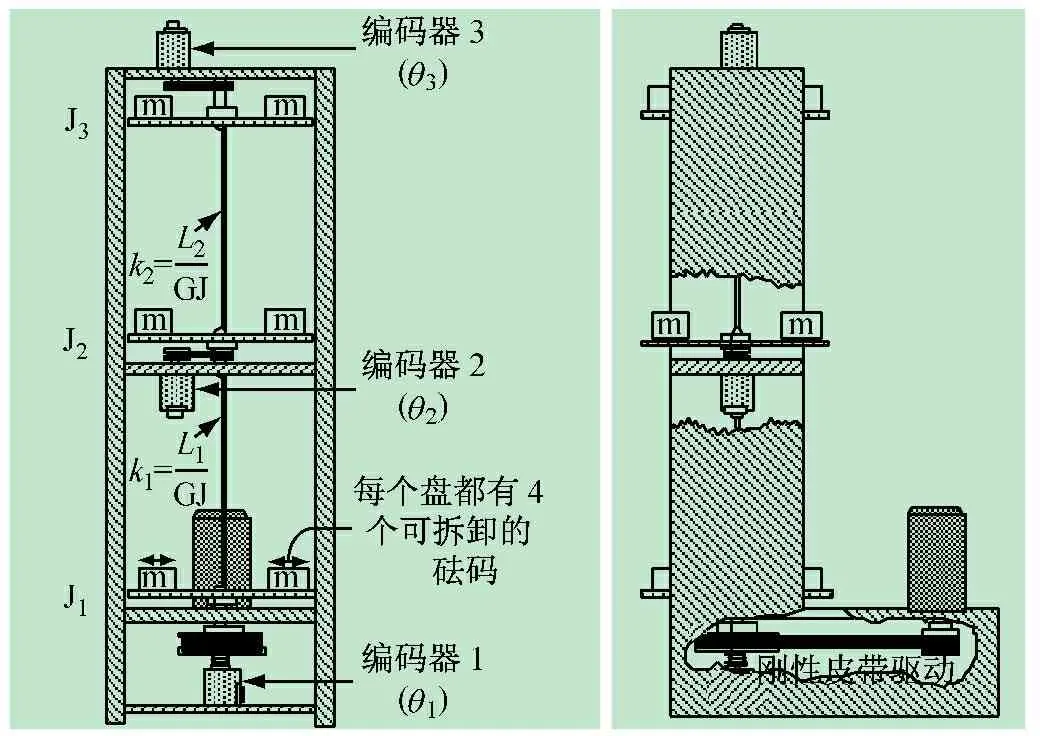
圖2 扭轉振動裝置的機械部分

(2) M56000系列的DSP控制器板卡和輸入輸出電箱組成的控制系統。如圖3所示，DSP控制器能夠以高采樣率來執行控制律，解釋軌跡命令，并支持數據采集、軌跡生成、系統狀態及安全檢測等功能。板卡中還包括可以實現編碼器脈沖解碼邏輯門陣列和2個進行實時模擬信號測量的輔助數模轉換器(DAC)。控制器的板卡與實際工業控制中使用的板卡相同。電箱主要功能是為機械部提供驅動電壓，同時接收編碼器的反饋信號，返回到控制器的板卡上，進而為執行程序提供測試數據。

圖3 控制系統部分

(3) 系統執行軟件。系統執行軟件即應用軟件和用戶界面，它支持控制器指定、軌跡定義、數據采集、繪圖系統執行指令等功能。執行軟件支持使用直觀的“類C”語言來編寫控制器算法程序，并且運行控制器。內置的自動編譯器為執行程序代碼的提供有效傳送和運行。此外，該執行軟件還提供了與其他應用軟件的接口，可以與Matlab軟件進行連接調試。執行軟件的運行窗口如圖4所示。

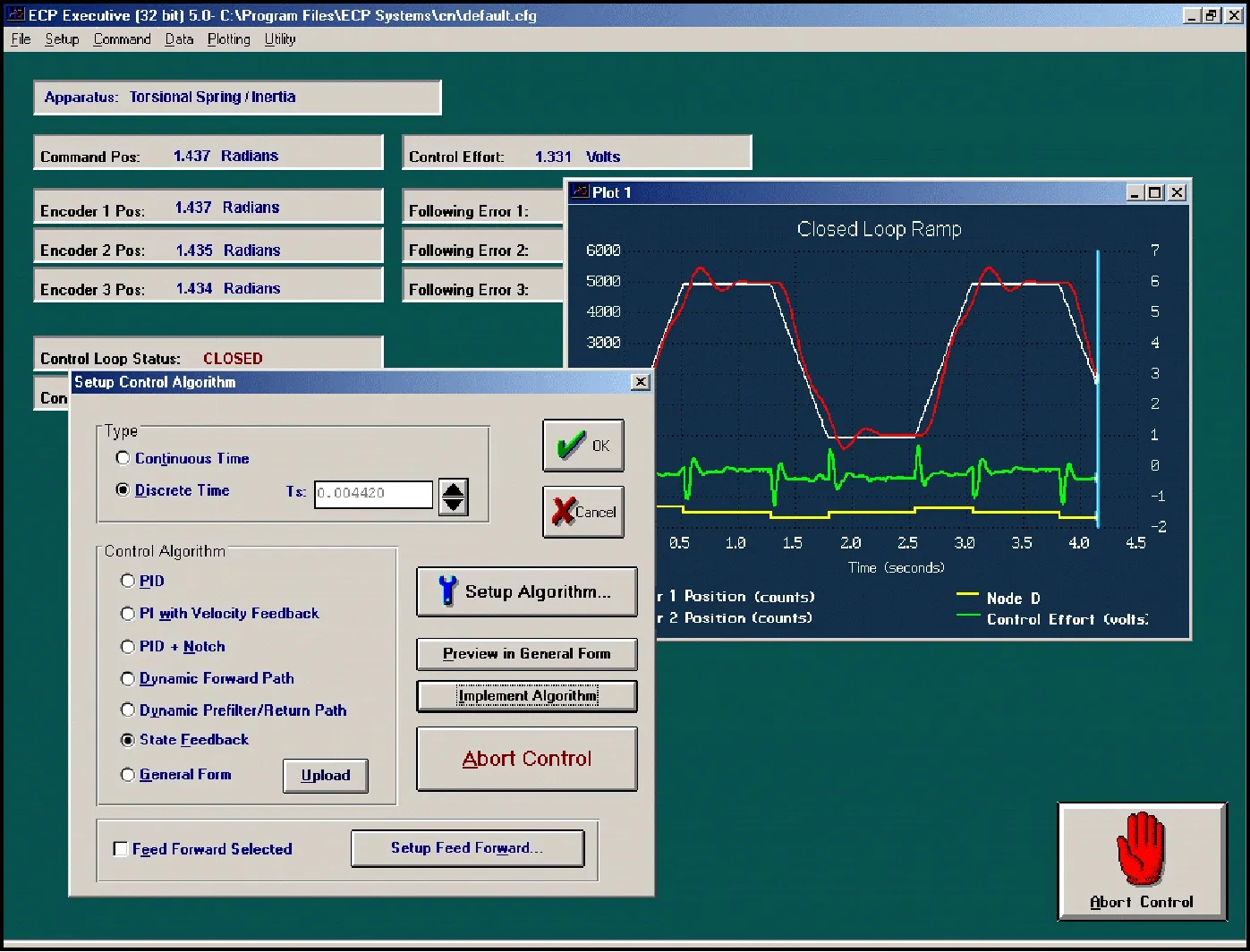
圖4 執行軟件的運行窗口

用戶可以編寫執行程序中的控制算法，然后將其加載到基于DSP的實時控制板卡上，DSP在每個指定的采樣周期執行此算法，讀取參考輸入和反饋傳感器(光電編碼器)的值，經過計算將數字控制效果信號輸出到DAC，DAC將數字流轉換為一個模擬電壓，然后通過一個伺服放大器轉換為電流，再通過電機變為轉矩，電機根據設備動力學特性將電機的輸入轉變為所期望的輸出。設備完成指定的動作后，傳感器的測試數據通過電箱回傳到執行軟件中，用于繪圖和存儲。

2 雙自由度對象的模型推導

實驗裝置可配置為雙自由度的系統，如圖5所示(忽略摩擦)。輸入為轉矩T(t)，輸出為第1個圓盤的角度θ1(t)和第2個圓盤的角度θ2(t)，2個圓盤的慣量分別為J1和J2，彈簧的彈性系數為k1。

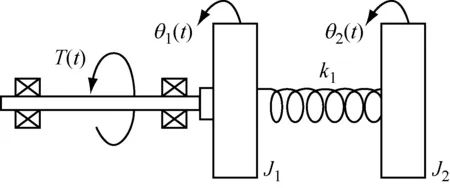
對2個圓盤進行受力分析及根據牛頓第二定律得到運動方程為：

(1)

對上式兩邊取拉普拉斯變換，并假設初始條件為零，得到傳遞函數為：

(2)

用狀態空間法表示為

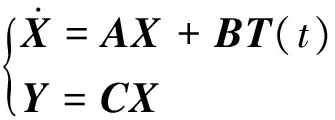
(3)

其中：

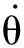
當Y=Xi(i=1,2,3,4),且其余量為零時，ci=1(i=1,2,3,4)。

通過數學模型可知，該模型為四階二型的系統，結構可以看成是剛體加一階振蕩模態組成，可以模擬單輸入單輸出、單輸入多輸出的系統。對于該模型的進行控制算法的研究，具有重要的應用意義。

3 LQR控制器的設計及仿真驗證

LQR(Linear Quadratic Regulator)最優設計指的是設計出的狀態反饋控制器K要使二次型目標函數J達到最小值，其中K由權矩陣Q與R唯一決定，因此對于參數Q和R的選擇十分重要。通過LQR方法，可以得到狀態線性反饋的最優控制規律，易于構成閉環最優控制。對于線性系統的控制器設計問題，如果其性能指標是狀態變量和控制變量的二次型函數的積分，則這種動態系統的最優化問題稱為線性系統二次型性能指標的最優控制問題，簡稱為線性二次型最優控制問題或線性二次問題。其最優解可以寫成統一的解析表達式以實現求解過程的規范化，并可簡單地采用狀態線性反饋控制律構成閉環最優控制系統，同時能夠兼顧多項性能指標，因此受到控制界學者的廣泛關注，并且在一些實驗裝置中獲得了應用[15-16]。

針對雙自由度的扭轉控制裝置，設計LQR控制器來對其進行控制，并通過在裝置上的實驗來驗證控制律的有效性。

3.1 LQR控制器設計

利用式(2)雙自由度對象傳遞函數可得到LQR控制的閉環系統頻域結構框圖，見圖6(a)。系統的輸出為第2個圓盤的角度θ2(t)，反饋信號選擇為θ1(t)和θ2(t)，對應反饋通道的為2個一階微分環節，傳遞函數為k1+k2s和k3+k4s，閉環回路傳遞函數為：

(4)

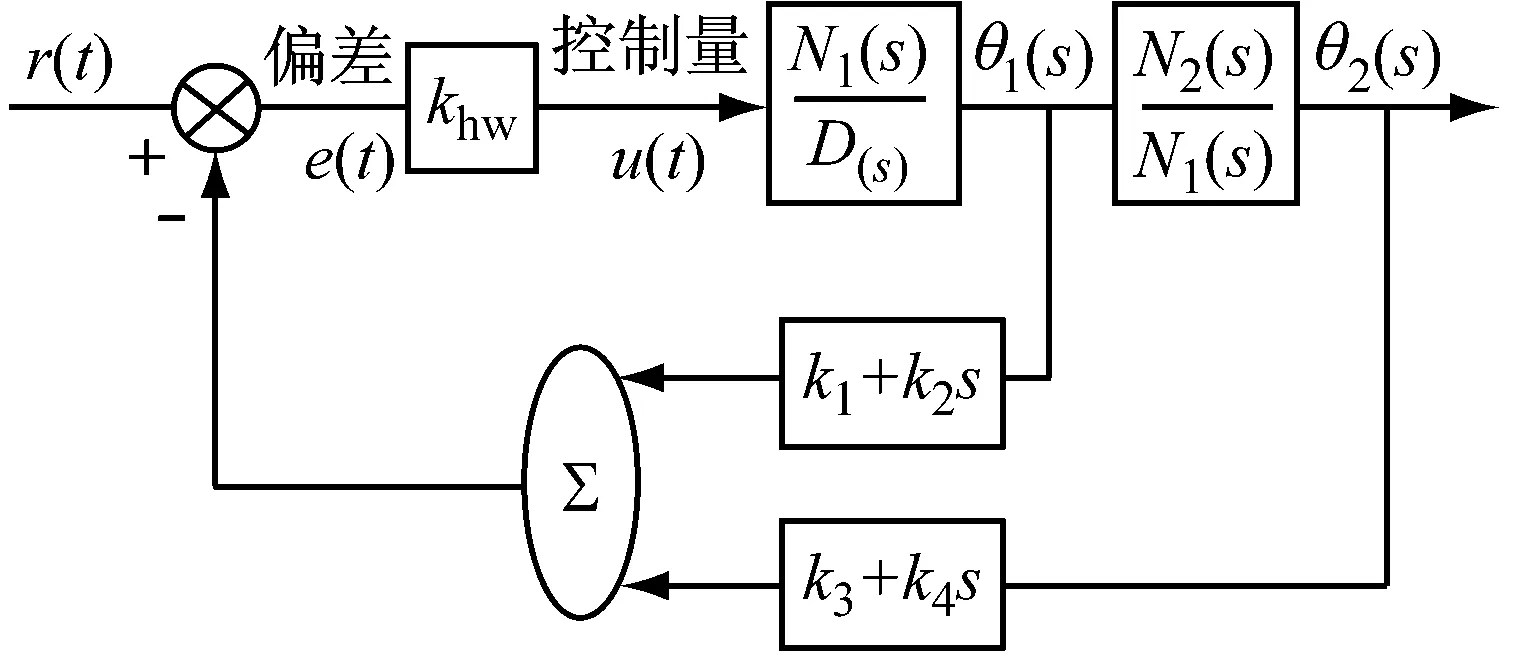
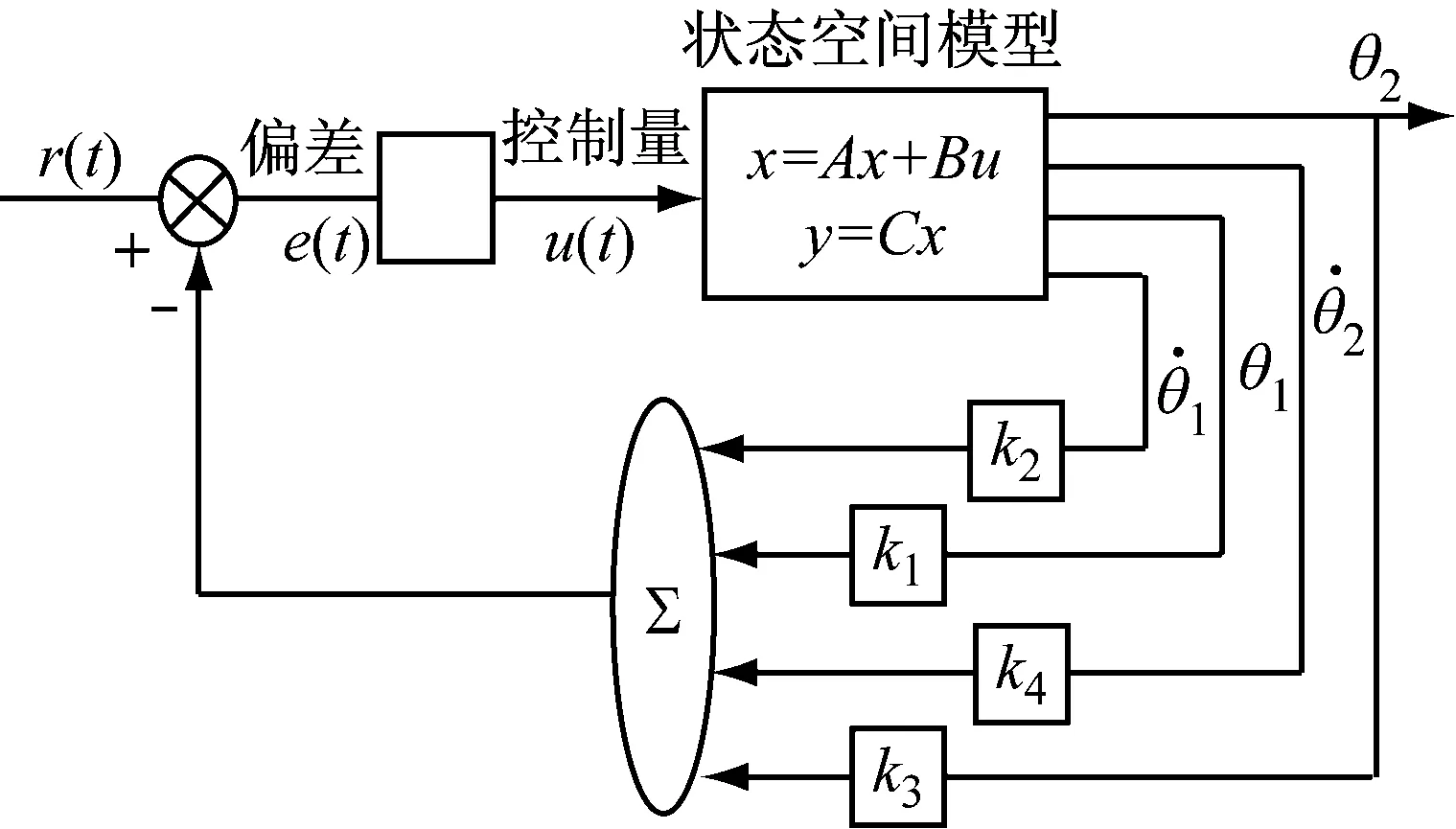
圖6(b)給出了雙自由度對象的全狀態反饋控制的閉環時域結構圖，對象使用式(3)給出的狀態空間模型描述，khw表示裝置的硬件增益，狀態選擇為圓盤1和2的角度和速度，輸出選擇為θ2(t)，系統為單入單出系統，則輸出矩陣選擇：

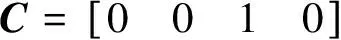
(5)

利用全狀態反饋控制設計一個LQR控制器，設計反饋率：

u=-Kx

(6)

其中：K=[K1K2K3K4]，線性二次型性能指標函數選擇為

(7)

設計目標是對于給定已知的Q和R，找到能最大限度減小指標函數的控制器K，

K=R-1BTP

(8)

其中，P滿足如下代數黎卡提方程：

ATP+PA-PBR-1BTP+Q=0

(9)

通過求解黎卡提方程就可以得到P和K，進而實現LQR控制。至此，針對雙自由度對象完成了LQR控制器的設計。

3.2 LQR控制器參數計算

在圖6(b)中，對象狀態空間模型的參數矩陣A，B由式(3)給出，其中,J1,J2表示圓盤的轉動慣量;k1表示彈簧系數，均為已知參數，則:

(10)

(11)

根據式(5)，參數Q選取為

(12)

這種參數選擇可以使出現在輸出θ2(t)誤差減小，并且可以降低控制量的損耗。然后設定6種情況下的控制量權值R：R=100，10，1.0，0.1，0.01和0.001。

為求解黎卡提方程，使用Matlab軟件中的函數

[K,P,E]=LQR(A,B,Q,R)

(13)

將參數A,B,Q,R代入上式，可得出每種情況下的K值以及閉環極點E，即[A-BK]的特征值。繪制出6種不同情況對應的閉環極點的圖形。

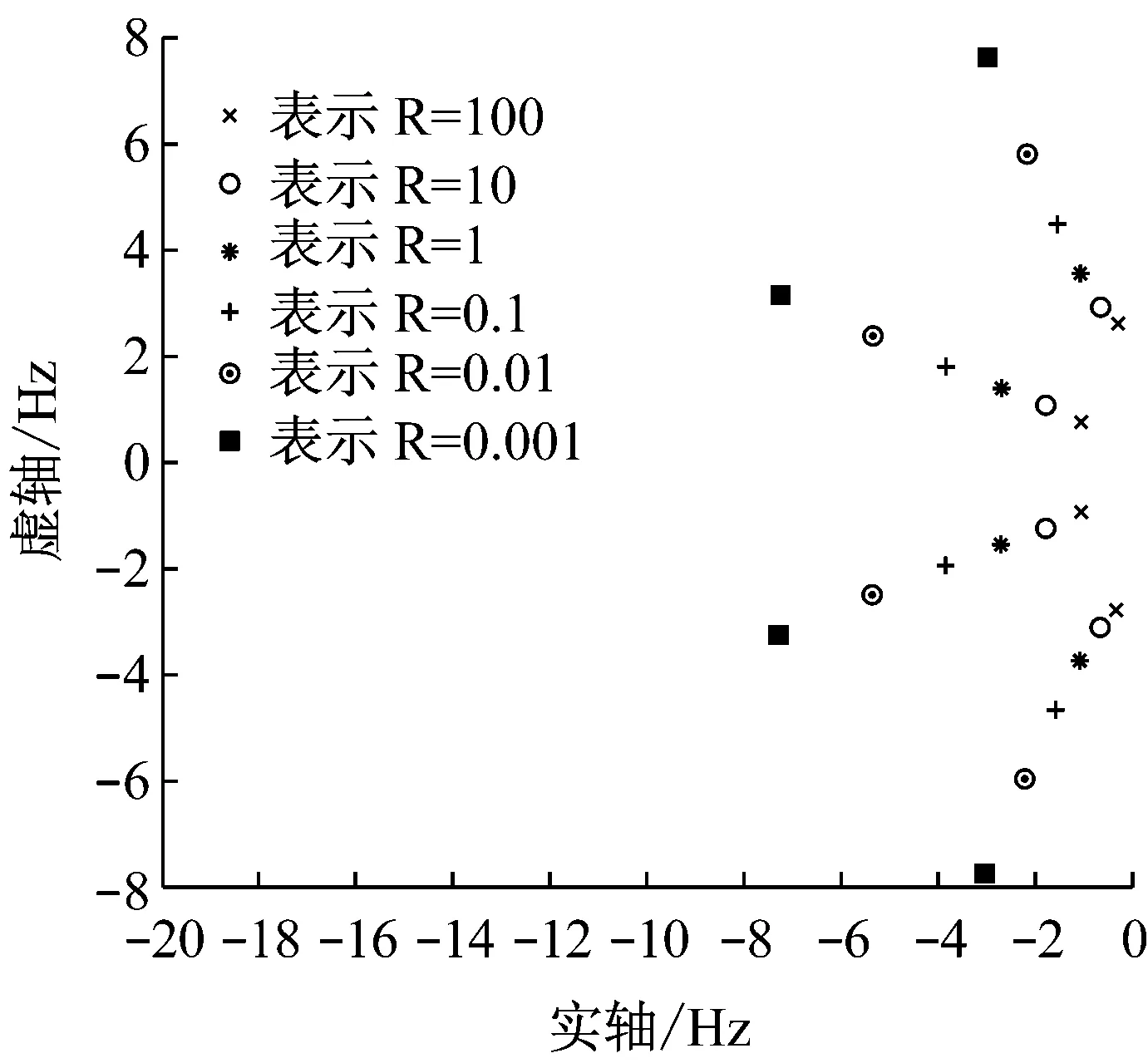
從所得數據中選擇一個最低極點頻率位于2.75～3.25 Hz間的閉環極點。使用該極點對應的K值，要求分量中K1和K3的值不要大于1，K2和K4的值不要大于0.12。得到的符合上述要求的合適的控制器是R=10時的情況，計算的控制器K為

K=[0.717 0 0.029 4 0.283 0 0.084 7]

3.3 仿真驗證

通過系統辨識的實驗，可以確定khw的值。將計算得到的控制器K參數輸入到軟件中，得到一個閉環的控制系統。

仿真步驟：設置輸入幅值為1 000，持續時間為2 s，重復次數為1的階躍信號；選擇控制器類型為State Feedback，分別輸入控制器K1、K2、K3、K4的參數，并加載到控制器中，設置數據采集，繪制編碼器1、2和給定位置的數據，得到對象的階躍響應曲線如圖8所示。由響應圖形可知，系統響應速度較快，超調量也比較小，證明所設計的LQR控制器具有良好的控制性能。

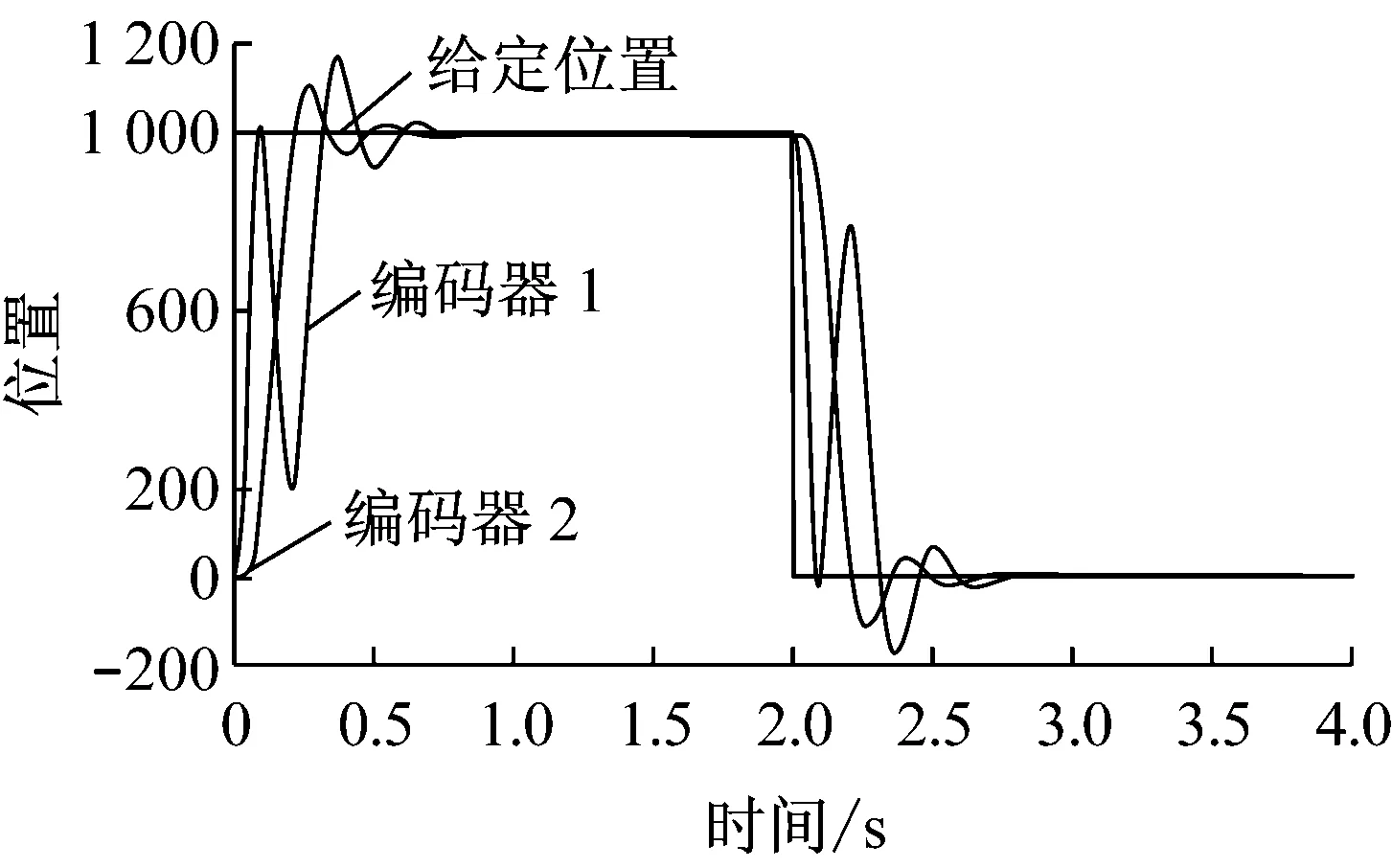
4 結 語

本文首先對美國ECP公司的扭轉振動裝置的系統組成、性能和所能實現的功能進行概要介紹。然后對于該裝置的一種等效的雙自由度系統模型，設計了LQR控制器，并驗證了控制器的效果。本實驗加深了對現代控制理論中的控制器設計方法的理解，為學生進一步學習更復雜的控制方法打下基礎。

[1] 謝誕梅，劉占輝，楊長柱，等.汽輪發電機組軸系扭轉振動對機械參數的敏感性分析 [J]. 動力工程，2005，25(4): 462-465.

XIE Dan-mei，LIU Zhan-hui，YANG Chang-zhu，etal. Sensitivity Analysis of the Torsional Vibration Behavior of a Turboset’s Rotor System to Changes of Its Mechanical Parameters [J]. Journal of Power Engineering，2005，25(4): 462-465.

[2] 劉 寶，楊雪靜，李 巖. 汽輪發電機組軸系扭振動態響應計算分析[J]. 機電工程技術，2011，40(12): 70-74.

LIU Bao，YANG Xue-jing，LI Yan. Calculation and Analysis of Dynamic Response of Steam Turboset Shafting [J]. Mechanical & Electrical Engineering Technology，2011，40(12): 70-74.

[3] 胡俊宏，高 峰，孫振魯. 汽輪發電機組軸系扭振模擬試驗臺研制[J]. 機械設計與制造，2012(10): 96-98.

HU Jun-hong，GAO Feng，SUN Zhen-lu. The Development of an Experiment Rig for Studying Torsional Vibration[J]. Machinery Design & Manufacture，2012(10): 96-98.

[4] 蘇永麗，康積濤，吳小剛. 汽輪發電機軸系扭振模態分析 [J]. 電氣開關，2013(5): 66-69.

SU Yong-li，KANG Ji-tao，WU Xiao-gang. Shaft Torsional Vibration Mode Prediction of Turbine Generator [J]. Electric Switchgear，2013(5): 66-69.

[5] 于學華. 發動機曲軸系統扭轉振動分析 [J]. 汽車技術，2008(3): 15-18.

YU Xue-hua. Analysis of Torsional Vibration in Crank shaft System [J]. Automobile Technology，2008(3): 15-18.

[6] 張 芳，王必璠，李顯戴. 車用發動機扭轉振動的分析與控制[J]. 汽車科技，2011(2): 47-51.

ZHANG Fang，WANG Bi-fan，LI Xian-dai. Torsional Vibration Analysis and Control for Engine on Vehicle [J]. Auto Mobile Science & Technology，2011(2): 47-51.

[7] 車定新. 發動機曲軸扭振計算與實驗分析研究[D]. 廣州： 華南理工大學， 2012.

[8] 陳 翔，崔志琴. 發動機曲軸軸系扭振技術研究的方法分析[J]. 機械工程與自動化，2012(6): 216-217.

CHEN Xiang，CUI Zhi-qin. Current Situation and Prospect of Engine Crankshaft Torsional Vibration technology Research [J]. Mechanical Engineering & Automation，2012(6): 216-217.

[9] 周金宇，陳占福. 粗軋機主傳動扭振分析[J]. 鋼鐵，2007，42(5): 51-54.

ZHOU Jin-yu，CHEN Zhan-fu. Torsional Vibration Analysis of Rougher Main Driving System of Rolling Mills [J]. Iron & Steel，2007，42(5): 51-54.

[10] 王 勤. 軋機主傳動系統的扭振分析與建模[J]. 冶金設備，2009(4): 6-9.

WANG Qin. Analysis and Modeling about Torsion Vibration for Main Drive System of Mill [J]. Metallurgical Equipment，2009(4): 6-9.

[11] 劉浩然，張業寬，李曉梅. 軋機非線性傳動系統沖擊扭振的研究與抑制[J]. 振動與沖擊，2010，29(7): 179-183.

LIU Hao-ran，ZHANG Ye-kuan，LI Xiao-mei，etal. Investigation and Suppression of Impact Torsional Vibration of a Rolling Mill’s Nonlinear Drive System [J]. Journal of Vibration and Shock，2010，29(7): 179-183.

[12] 郁 飛，王天榮，許 勃. 激光扭振儀調整、應用與誤差分析[J]. 實驗室研究與探索，2001，20(4): 57-58.

YU Fei，WANG Tian-rong，XU Bo. Adjustment, Application and Error Analyzing of the Torsional Vibration Meter [J]. Research and Exploration in Laboratory，2001，20(4): 57-58.

[13] 王炳輝，馮志敏，胡志鋼. 智能多通道的軸系扭振試驗臺[J]. 實驗室研究與探索，2004，23(2): 41-43.

WANG Bing-hui，FENG Zhi-min，HU Zhi-gang. An Intelligent Multichannel Shafting Torsional Vibration Tester[J]. Research and Exploration in Laboratory，2004，23(2): 41-43.

[14] 劉振峰，常 非. 柔性軸扭振系統實驗臺及其實驗[J]. 實驗室研究與探索，2009，28(8): 45-47.

LIU Zhen-feng，CHANG Fei. Research on Flexible Torsional System Design Methods [J]. Research and Exploration in Laboratory，2009，28(8): 45-47.

[15] 李勁松，顏國正，馮劍舟,等. 基于線性二次型最優控制策略的倒立擺實驗系統搭建[J]. 實驗室研究與探索，2010，29(3): 38-40.

LI Jin-song，YAN Guo-zheng，FENG Jian-zhou ，etal. Construction of the Inverted-Pendulum Experimental System Based on LQR [J]. Research and Exploration in Laboratory，2010，29(3): 38-40.

[16] 袁 浩，劉繼光，李保林. LQR 控制策略在旋轉機架模型中的應用[J]. 實驗室研究與探索，2010，29(3):54-56.

YUAN Hao， LIU Ji-guang， LI Bao-lin. Application of LQR Control Strategy in a Rotary Gantry System [J]. Research and Exploration in Laboratory，2010，29(3): 54-56.