基于仿真的FFS設(shè)備能力優(yōu)化配置*
范飛龍,李 翔,2
(1.廣東工業(yè)大學(xué)廣東省計(jì)算機(jī)集成制造系統(tǒng)重點(diǎn)實(shí)驗(yàn)室,廣東廣州 510006;2湖南省湘南學(xué)院物理與電子信息工程系,湖南郴州 423000)
基于仿真的FFS設(shè)備能力優(yōu)化配置*
范飛龍1,李 翔1,2
(1.廣東工業(yè)大學(xué)廣東省計(jì)算機(jī)集成制造系統(tǒng)重點(diǎn)實(shí)驗(yàn)室,廣東廣州 510006;2湖南省湘南學(xué)院物理與電子信息工程系,湖南郴州 423000)
首先,以制造系統(tǒng)的最小總投資成本為目標(biāo)函數(shù)、系統(tǒng)的平均產(chǎn)出率為約束條件構(gòu)建設(shè)備能力優(yōu)化配置問(wèn)題的數(shù)學(xué)模型。其次,鑒于該數(shù)學(xué)模型中約束條件的數(shù)學(xué)表達(dá)式難以用決策變量(設(shè)備數(shù)量)的封閉形式加以描述的難題,運(yùn)用eM-plant軟件搭建仿真平臺(tái)進(jìn)而計(jì)算出系統(tǒng)的平均產(chǎn)出率。然后,運(yùn)用分支定界法精確求解CCP問(wèn)題。最后,通過(guò)對(duì)實(shí)例的求解分析驗(yàn)證求解方法的實(shí)用性和有效性。
設(shè)備能力優(yōu)化配置(CCP);仿真;分支定界法
0 引言
目前而言,個(gè)性化的客戶訂單和及時(shí)化的交貨期嚴(yán)重困擾并制約著定制型裝備制造企業(yè)的生存發(fā)展。為了在競(jìng)爭(zhēng)激烈的市場(chǎng)環(huán)境下獲取盡可能多的客戶訂單,訂單交貨期已上升到與產(chǎn)品報(bào)價(jià)同等重要的地位[1]。為了能夠及時(shí)響應(yīng)個(gè)性化的訂單,企業(yè)通常購(gòu)買(mǎi)大量具備復(fù)合型、智能型等現(xiàn)代特征的加工設(shè)備。然而現(xiàn)實(shí)情況是,企業(yè)領(lǐng)導(dǎo)層制定購(gòu)買(mǎi)設(shè)備的決策時(shí),經(jīng)常只是憑借經(jīng)驗(yàn)而缺乏足夠的理論依據(jù)。如此一來(lái),通常會(huì)發(fā)生如下兩種現(xiàn)象:其一,設(shè)備產(chǎn)能過(guò)剩,即是現(xiàn)有的設(shè)備加工能力大于客戶需求,使得加工設(shè)備的閑置率提高、利用率降低,從而造成資金的浪費(fèi);其二,設(shè)備產(chǎn)能不足,即是現(xiàn)有的設(shè)備加工能力難以滿足客戶需求,客戶的訂單便無(wú)法及時(shí)交付,甚至影響到企業(yè)的信譽(yù)度。
文獻(xiàn)[2]將制造系統(tǒng)最優(yōu)化問(wèn)題總結(jié)為三類,即在滿足系統(tǒng)性能約束指標(biāo)下實(shí)現(xiàn)加工設(shè)備總投資額的最小化、在滿足優(yōu)先投資預(yù)算下使系統(tǒng)的某項(xiàng)指標(biāo)最優(yōu)化、將制造系統(tǒng)拆分成若干制造單元并以此來(lái)改善制造系統(tǒng)總體性能。文獻(xiàn)[3]研究訂貨型車間的任務(wù)投放問(wèn)題,對(duì)有限緩存無(wú)阻塞的情形進(jìn)行仿真,并對(duì)每道工序有一臺(tái)或多臺(tái)加工設(shè)備的兩級(jí)Flow Shop問(wèn)題進(jìn)行了探討。文獻(xiàn)[4]研究確定性環(huán)境下連續(xù)需求的能力優(yōu)化配置問(wèn)題,以實(shí)現(xiàn)設(shè)備配置成本的最小化為目標(biāo),以滿足生產(chǎn)需求為約束條件,提出了一種排序決策方法,用分枝定界方法和啟發(fā)式方法對(duì)能力配置問(wèn)題進(jìn)行求解。文獻(xiàn)[5]研究工業(yè)企業(yè)的設(shè)備能力優(yōu)化配置問(wèn)題,以收集、分析以及整理生產(chǎn)實(shí)際數(shù)據(jù)為基礎(chǔ),建立仿真模型,通過(guò)分析仿真結(jié)果尋找生產(chǎn)瓶頸。文獻(xiàn)[6]基于車輛能力規(guī)劃系統(tǒng),將能力優(yōu)化配置問(wèn)題轉(zhuǎn)換成一個(gè)受時(shí)間窗約束的車輛路徑規(guī)劃問(wèn)題并進(jìn)行仿真建模,并使用禁忌搜索算法對(duì)模型進(jìn)行求解。
仿真法是在一系列近乎真實(shí)的假設(shè)和前提下,求解制造系統(tǒng)的性能指標(biāo)。針對(duì)約束函數(shù)無(wú)法用決策變量的封閉形式加以表達(dá)的難題,可以使用狀態(tài)空間分解法或者擴(kuò)展近似法等方法加以解決。本文擬采用分支定界算法求解CCP問(wèn)題,考慮到近似算法可能對(duì)最終結(jié)果產(chǎn)生影響,求解約束性能指標(biāo)時(shí)使用仿真法。
1 數(shù)學(xué)描述
1.1 條件假設(shè)及目標(biāo)函數(shù)
本文從企業(yè)的實(shí)際情況抽象出一個(gè)單種類產(chǎn)品多級(jí)FFS典型制造系統(tǒng)模型,具體如圖1所示。該車間有多道加工工序,且每級(jí)設(shè)備前設(shè)置一個(gè)公共緩沖區(qū)(有限容量)。

圖1 定制型裝備柔性流水車間排隊(duì)網(wǎng)通用模型
在數(shù)學(xué)模型建立前,先作如下假設(shè):
①同類型設(shè)備的單價(jià)相同;
②工件以“泊松流”的方式到達(dá)制造系統(tǒng);
③產(chǎn)品的加工工藝已知;
④設(shè)備的加工時(shí)間服從負(fù)指數(shù)分布,且彼此之間相互獨(dú)立;
⑤工件之間彼此相互獨(dú)立;
⑥一臺(tái)設(shè)備僅能同時(shí)加工一個(gè)工件;
⑦各節(jié)點(diǎn)緩存(buffer)容量有限。
1.2 數(shù)學(xué)模型
CCP問(wèn)題的主要研究?jī)?nèi)容是在企業(yè)現(xiàn)有的資源條件下,以系統(tǒng)的平均產(chǎn)出率作為約束條件,對(duì)加工設(shè)備優(yōu)化配置以使設(shè)備總成本最小化。該優(yōu)化問(wèn)題的數(shù)學(xué)模型表述如下:

對(duì)模型(1)的各個(gè)參數(shù)作如下定義:
xi:表示制造系統(tǒng)第i級(jí)設(shè)備的數(shù)量;ci:表示制造系統(tǒng)第i級(jí)設(shè)備的單價(jià);:表示制造系統(tǒng)總設(shè)備成本;:表示制造系統(tǒng)的平均產(chǎn)出率;Θ*:表示制造系統(tǒng)的預(yù)設(shè)產(chǎn)能;?:表示隨機(jī)元。
不難得出CCP問(wèn)題的特點(diǎn):(1)約束函數(shù)表達(dá)式難以用設(shè)備數(shù)量的封閉形式表達(dá);(2)該問(wèn)題是隨機(jī)整數(shù)規(guī)劃問(wèn)題。特點(diǎn)1加大了求解模型的難度,為了能夠有效地求解系統(tǒng)的平均產(chǎn)出率,本文使用eM-plant軟件搭建仿真平臺(tái)來(lái)計(jì)算模型的約束指標(biāo)。根據(jù)特點(diǎn)(2),本文擬采用分支定界法。
2 設(shè)備能力優(yōu)化配置仿真建模
2.1 仿真模型建立
采用eM-Plant仿真軟件(Tecnomatix Plant Simulation8.2)搭建仿真實(shí)驗(yàn)平臺(tái),硬件配置如下:雙核CPU 2.0GHz,2G內(nèi)存,如圖2所示。
仿真系統(tǒng)由四個(gè)制造單元組成,工件均在訂單源產(chǎn)生。工件首先根據(jù)第一級(jí)加工設(shè)備前的緩存堵塞狀況判斷工件進(jìn)入緩存(B1),或者根據(jù)加工設(shè)備的狀態(tài)判斷是否進(jìn)入加工設(shè)備加工,如果第一級(jí)緩存(B1)已滿,且第一級(jí)各加工設(shè)備上均有工件,則由訂單源產(chǎn)生的工件進(jìn)入Buffer0(無(wú)限容量)。表示訂單源,服從泊松分布;表示緩存,其大小可根據(jù)實(shí)際需要進(jìn)行靈活調(diào)整;表示加工設(shè)備,每級(jí)設(shè)備的數(shù)量可根據(jù)優(yōu)化配置的結(jié)果不斷進(jìn)行調(diào)整;用來(lái)獲取穩(wěn)定狀態(tài)下的平均產(chǎn)出率。

圖2 Tecnomatix Plant Simulation8.2仿真系統(tǒng)
2.2 分支定界法
前人經(jīng)常使用分支定界算法求解線性整數(shù)規(guī)劃(Linear Integer Programming,ILP)問(wèn)題,目前求解ILP問(wèn)題的軟件大多以分支定界算法為其核心思想,如LINDO Xpress-MP、、CPLEX等等[7]。一般ILP問(wèn)題p0的數(shù)學(xué)模型表述如下:

其中,c∈Rn,A∈Rm×n,b∈Rm,x為決策變量。
一般的分支定界法求解步驟如圖3所示。

圖3 分支定界法求解步驟
為了更形象地描述本文所使用的分支定界算法,將分支示意圖描述如圖4所示。
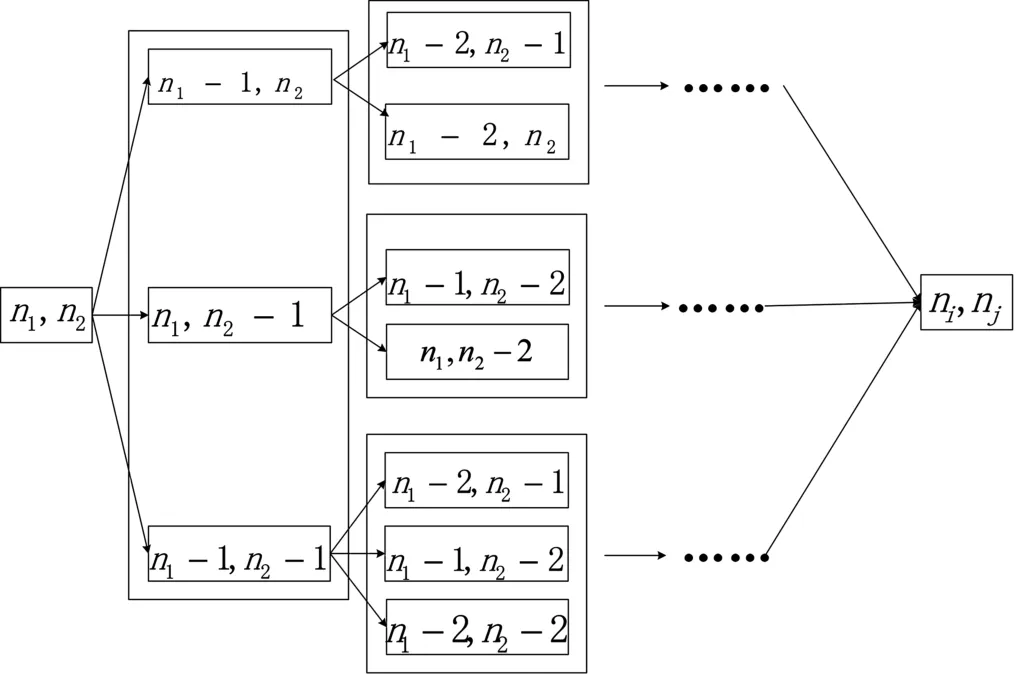
圖4 分支定界求解示意圖
即二級(jí)系統(tǒng)每級(jí)的設(shè)備數(shù)量分別為n1和n2,該設(shè)備組合向量(n1,n2)是可行解。在對(duì)其進(jìn)行優(yōu)化配置時(shí),首先分成3支,即(n1-1,n2)、(n1,n2-1)和(n1-1,n2-1),判斷三者是否均為可行解,如果均是可行解,則選擇是制造系統(tǒng)總成本最小(n1-1,n2-1)的一支作為較優(yōu)解繼續(xù)進(jìn)行分支,同時(shí)將(n1-1,n2)、(n1,n2-1)所對(duì)應(yīng)的目標(biāo)函數(shù)值作為上界;如果三者均為不可行解,則(n1,n2)即為最優(yōu)解,如果(n1-1,n2) 和 (n1,n2-1) 是可行解,(n1-1,n2-1)不是可行解,則將(n1-1,n2-1)所對(duì)應(yīng)的目標(biāo)函數(shù)值作為下界,同時(shí)從(n1-1,n2)和(n1,n2-1)選擇目標(biāo)函數(shù)值最小的一支繼續(xù)分解,另一支所對(duì)應(yīng)的目標(biāo)函數(shù)值作為上界。以此類推,直至找到最優(yōu)解(ni,nj),此時(shí)(ni,nj)的所有分支均是不可行解。
3 算例分析
3.1 算例數(shù)據(jù)
針對(duì)CCP問(wèn)題的具體特征,本文構(gòu)建的算例主要包括工件到達(dá)率(λ)、設(shè)備類型、設(shè)備數(shù)量(ni)、設(shè)備單價(jià)(ci)等信息。具體如表1所示。
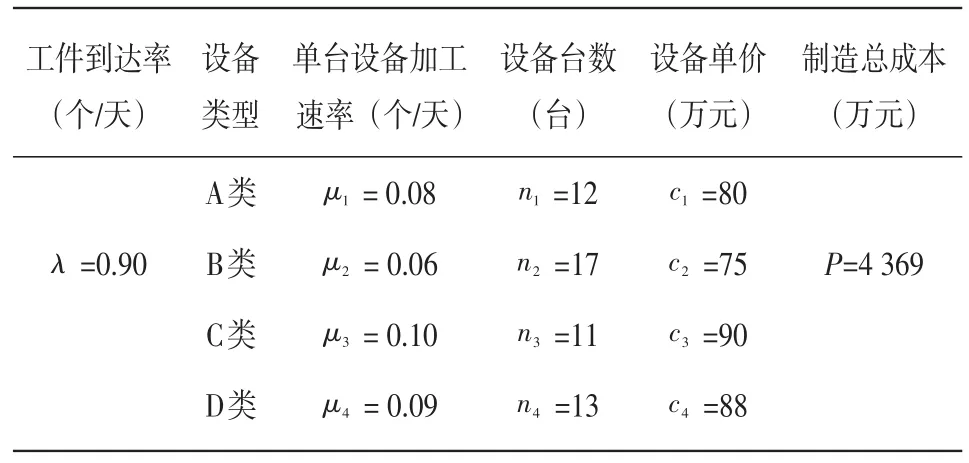
表1 初始參數(shù)設(shè)定
另外,在求解CCP問(wèn)題時(shí),應(yīng)該首先確定系統(tǒng)各級(jí)的buffer容量,即各級(jí)設(shè)備前公共緩沖區(qū)的容量。具體如表2所示。

表2 buffer容量設(shè)定
另外,由表1得知系統(tǒng)平均產(chǎn)出率為0.9。一般而言,真實(shí)的設(shè)備產(chǎn)出率與無(wú)限緩存下系統(tǒng)的平均產(chǎn)出率之間的關(guān)系比例值為0.9,即Θ*=0.9× 0.9=0.81。
CCP問(wèn)題的算例需遵守如下規(guī)則:
(1)各級(jí)設(shè)備的加工能力之和原則

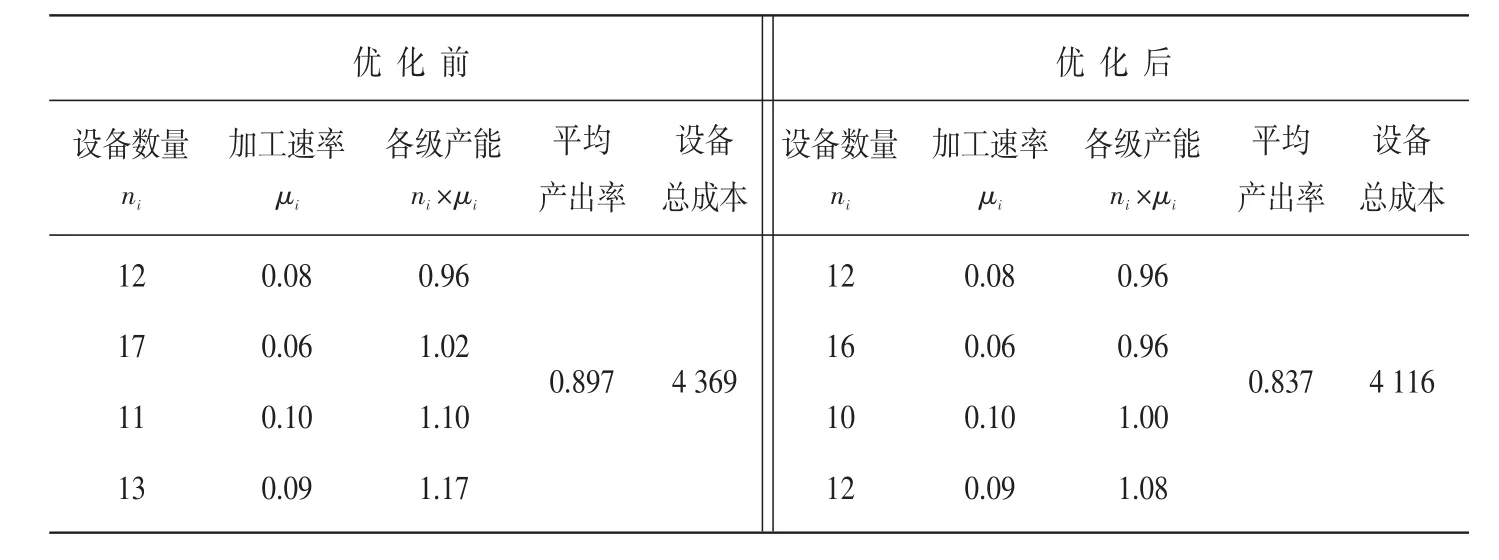
表3 CCP問(wèn)題優(yōu)化前后對(duì)比

式子(1)表示各級(jí)設(shè)備的加工能力之和(μi×ni)應(yīng)大致相等,式子(2)表示各級(jí)設(shè)備的加工能力之和(μi×ni)應(yīng)呈“倒喇叭形”且略大于工件到達(dá)率(λ)。由表1知, μ4×n4=1.17、μ3×n3=1.10、 μ2≥n2=1.02、 μ1×n1=0.96、 λ= 0.90。不難看出,從加工能力原則看,算例是合理的。

圖5 優(yōu)化前、后設(shè)備數(shù)量變化圖
(2)各級(jí)緩沖區(qū)的容量原則
前面工序被阻塞的概率比后面大,對(duì)緩沖區(qū)容量進(jìn)行設(shè)置時(shí),前面緩沖區(qū)容量需大于(或等于)后面的緩沖區(qū)容量,即B4+n4≤B3+n3≤B2+n2≤B1+n1。 由 表 1知 ,B4+n4=18 、 B3+n3=18 、 B2+n2=33 、B1+n1=46。不難看出,從緩沖區(qū)容量原則看,算例也是合理的。
3.2 結(jié)果對(duì)比與分析
由表3知,優(yōu)化前、后設(shè)備組合向量分別為:Xf=(12,17,11,13)T、Xa=(12,16,10,12)T。為了形象地描述優(yōu)化的效果,本文運(yùn)用直方圖表示優(yōu)化前、后各級(jí)設(shè)備數(shù)量的變化,具體如圖5所示。
第一、二、三、四級(jí)設(shè)備分別減少了0、1、1、1臺(tái),共降低成本253萬(wàn)元。系統(tǒng)的平均產(chǎn)出率也得到一定程度的優(yōu)化,優(yōu)化前平均產(chǎn)出率為0.897,比系統(tǒng)預(yù)設(shè)產(chǎn)能超出了9.7%;優(yōu)化后平均產(chǎn)出率為0.837,比系統(tǒng)預(yù)設(shè)產(chǎn)能超出了3.2%。
由表3知,優(yōu)化后的各級(jí)產(chǎn)能分別為:μ4×n4=1.08、 μ3×n3=1.00、 μ2≥n2=0.96、μ1×n1=0.96;各級(jí)緩沖區(qū)容量: B4+n4=34、B3+n3=32、B2+n2=17、B1+n1=17。所以,優(yōu)化后的結(jié)果是合理的。
4 結(jié)束語(yǔ)
本文首先根據(jù)問(wèn)題特征建立數(shù)學(xué)模型,然后使用仿真法求解數(shù)學(xué)模型的約束性能指標(biāo),并在此基礎(chǔ)上使用分支定界算法精確求解CCP問(wèn)題,具有一定的工程價(jià)值。美中不足的是本文所使用的分支定界算法的核心——分支原則沒(méi)有產(chǎn)生高效的分支策略,在后續(xù)的研究中,筆者著重于CCP問(wèn)題的具體特征提出一種高效的分支策略。
[1]A.haskose,B G Kingsman,D worthington.Modelling flow and jobbing shops as a queueing network for work?load control[J].International Journal of Production Economics,2002,78(3):271-285.
[2]Bitran,G.R.,Morabito,R..An Overview of Trade-off Curves in Manufacturing System Design[J].Produc?tion and Operations Management, 1999, 8(1):56-75.
[3]陳田,陳慶新,毛寧,等.具有兩道工序的柔性同序加工車間任務(wù)投放策略[J].工業(yè)工程,2010,13(5):69-74.
[4]Neebe,A.W.,Rao,M.R.Sequencing Capacity Ex?pansion Projects in Continuous Time[J].Management Science,1986,32(11):1467-1479.
[5]Eneyo,E.S.,Pannirselvam,G.P.The use of simula?tion in facility layout design:a practical consulting expe?rience[C].1998.
[6]Loo,H.L.,et al.Vehicle capacity planning system:a case study on vehicle routing problem with time windows[J].Systems, Man and Cybernetics, Part A: Sys?tems and Humans, IEEE Transactions on.2003,33(2):169-178.
[7]于戰(zhàn)科,倪明放,汪澤焱,等.整數(shù)線性規(guī)劃的改進(jìn)分支定界算法[J].計(jì)算機(jī)應(yīng)用,2011,31(2):36-38.
Simulation-Based Capacity Configuration Optimization for Flexible Flow Shop
FAN Fei-long1,LI Xiang1,2
(1.Guangdong Provincial Key Laboratory of Computer Integrated Manufacturing System,Guangdong University of Technology,Guangzhou510006,China;2.Hunan Xiang Nan University Department of Physics&Electronic Information Engineering,Chenzhou423000,China)
First of all,construct the Mathematical model of capacity allocation optimization problem(capacity configuration problem,CCP)with the minimum total investment cost as objective function and the average output rate of the system as the constraint condition. Secondly,the mathematical expressions of constraint condition in this mathematical model is difficult to use closed form of the decision variables(equipment)to describe,the simulation platform is built up and then calculate the average output rate of the system by using Em-plant software.Then,using the branch and bound method to exactly solute of CCP problem.Finally,verify the practicality and effectiveness for solving method by solving the case analysis.
capacity configuration problem(CCP);simulation;branch-and-bound algorithm
TP391 F406
:A
:1009-9492(2014)10-0016-04
10.3969/j.issn.1009-9492.2014.10.005
范飛龍,男,1987年生,河南人,碩士研究生。研究領(lǐng)域:制造系統(tǒng)設(shè)計(jì)優(yōu)化。
(編輯:阮 毅)
*湖南省湘南學(xué)院院級(jí)重點(diǎn)教改項(xiàng)目
2014-04-01

