基于切比雪夫不等式的輸變電工程造價合理區間的計算方法

張戈力，溫衛寧，李培棟，任 妍，盧 玉，商 桑

(國網北京經濟技術研究院，北京市102209)

0 引 言

根據我國電網的發展規劃，電網企業將加快建設堅強智能電網，全力推進重點工程建設，以提高電網智能化水平。為了適應新的工程建設，保障項目建設順利開展，研究與之有關的造價水平的合理性分析方法，保障造價管理精益化水平不斷提高，對于電力企業的項目決策和社會經濟資源的合理利用都具有重要的理論和實踐意義。

在基建項目中，造價管理水平的高低直接決定著投資效益。現行的造價管理方法雖已較為完善，但在項目的規劃論證及技術經濟分析領域仍有一定的提高空間，缺少以數學理論及大量工程實際數據為基礎的定量分析依據。

電網基建工程的造價水平受到物價上漲、政策調整等方面影響會有一定上漲［1］，工程造價會出現一定變化，合理的工程造價水平是影響電力建設健康發展較為關鍵的因素，因此，控制電網工程造價水平的問題顯得較為突出［2］。

目前，電網工程造價水平分析方面的成果主要有:文獻［3］根據電網工程限額設計指標，對220 ～750 kV 電網工程做了分析;文獻［4］采用輸變電工程通用造價分析方法，對110 ～750 kV 電網工程進行分析等。這些方法以技術條件為計算基礎，較為貼近實際工程，在項目論證、經濟評價、造價管理等方面被廣泛地應用。

文獻［5］指出受到經濟條件、設備材料價格、建設外部環境影響，電網工程的造價是不斷變化的，應作較為深入的分析，為有效控制工程造價提供參考。處于不同地區的電網工程造價水平波動應在一定合理范圍內。掌握造價的合理范圍，可以直觀表現電網工程造價特性。合理區間可以作為工程前期論證的決策參考，指導工程造價工作，為多角度定量分析造價提供了新的方法。目前，尚未有一種深入分析造價合理區間的計算方法。

為此，本文提出造價合理區間的概念并給出其計算方法，基于可靠數據，該方法可以實現對全電壓等級造價合理水平的分析，具有較強的可用性。

1 輸變電工程造價的合理區間

1.1 造價合理區間的定義

分析輸變電工程中各電壓等級變電、線路工程的樣本數據時，為了得到一個具有代表性的造價合理水平區間作為造價控制的參考指標，根據相關專家經驗，定義使得大部分(頻數占總數至少80%)造價樣本數據落入的集中分布區間φ 為輸變電工程造價的合理區間，代表該地區這一電壓等級待建工程造價合理水平。

該造價合理區間指標可作為初步判別工程投資的依據，也可為制定投資計劃提供參考依據等，實現工程造價控制的可控、在控的要求。

1.2 造價合理區間的計算思路

論文提出的造價合理區間的計算分為3個步驟，包括樣本數據的特征值計算，采用箱線圖剔除樣本異常值［6］，根據切比雪夫定理［7］、單變量最優化法［8-9］計算造價合理區間。

統計輸變電工程中各電壓等級的變電、線路的工程總投資，根據總容量或總長度數據分別計算單位容量造價和單位長度造價，作為造價合理區間計算的原始樣本數據。

將變電、線路工程的數據樣本按照“電壓等級”、“所在地區”兩個條件進行劃分，其中線路工程分為“單回”和“雙回”兩種情況分析，如圖1 所示。

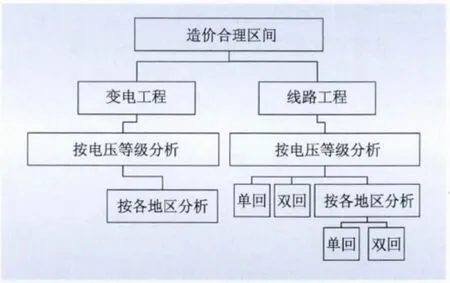
圖1 造價數據分析的分類方法Fig.1 Classification of cost data analysis

2 工程造價合理區間的計算方法

2.1 計算步驟

(1)計算該樣本數據的中位數、第一四分位數、第三四分位數，分析得到樣本數據的最大值、最小值，計算樣本數據的樣本均值、樣本方差［10］。

(2)采用箱線圖剔除異常值，對造價數據進行一次異常值分析，排除異常值以后，樣本數據將減少，樣本數據將更趨于合理，為下一步計算區間提供基礎數據。

(3)根據切比雪夫不等式原理，有至少80%的統計數據落在區間φ 中，即

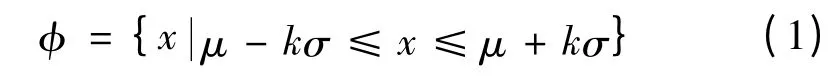
式中:μ 為樣本的平均值;σ 為樣本標準差;k 為區間系數。

此時k =2.24，將k 值作為造價合理區間的系數初值，利用一維參數尋優中的進退法迭代計算k 值的最優值，最終確定造價合理區間。

2.2 箱線圖

異常值是指樣本中的個別值，其數值明顯偏離其所屬的其余觀測值［11］。因為數據中的異常值常會對數據的計算帶來較大的拉動作用，如果不進行異常值篩選，分析結果有較大可能會偏離正常水平，所以應在分析計算之前篩除異常值。

箱線圖是由1 組數據的最大值、最小值、中位數和2個四分位數這5個特征值繪制而成的、反應原始數據分布的圖形。箱線圖提供了識別異常值的標準:異常值被定義為小于下四分位數QL減去1.5 倍四分位距離QIQR、大于上四分位數QU加上1.5 倍四分位距離QIQR，即Q ＜QBL或者Q ＞QBU，其中

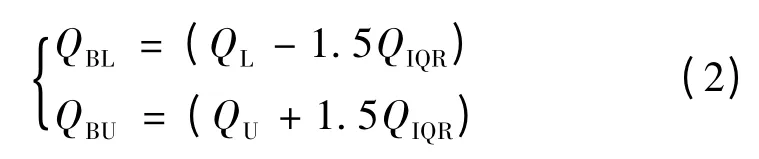
箱線圖判斷異常值的標準以四分位數和四分位距離為基礎，因為四分位數是一個固定位置的數據值，不容易受到數據異常變化的影響，異常值不能對這個標準施加較大影響。

在篩除了對樣本均值、樣本方差拉動作用較大的異常值后，再計算樣本均值及樣本方差得到的分析結果更能反映樣本數據的數理特點。

2.3 根據切比雪夫不等式確定k 值初值

對于任意分布形態的數據，根據切比雪夫不等式，至少有C 組數據落在k個標準差之內。切比雪夫不等式不要求明確樣本數據的分布情況，能夠確定數據所占百分比例C 的下限，樣本數據落入均值周圍k倍標準差［10］，即區間的百分比例至少為

由式(3)得到樣本值落入區間的百分比例，結果如表1 所示。

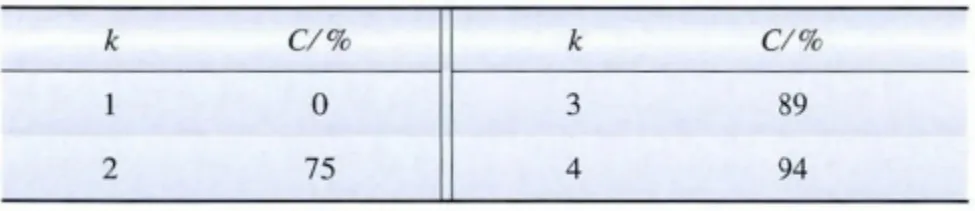
表1 樣本值落入區間的預測比例值Tab.1 Prediction ratio of sample values located in interval

由表1 可知:當C =80%時，即至少有80%的數據樣本落入區間時，系數k =2.24。如計算得到的區間包括了80%以上樣本數據，則可以通過調整系數k的值，使得造價區間趨于包括80%左右的樣本數據，即本文所提出的造價區間。

2.4 基于進退法參數尋優的合理區間計算

參數尋優方法較多，包括黃金分割法、割線法、拋物線插值法［12-14］，本文以一維參數尋優方法中的進退法為基礎，計算合理區間中的參數k。

進退法的計算思想是先從初值λ0出發，利用目標函數F(λ)的信息，來回仔細地搜索，以期求得無條件極值問題、即minF(λ)的最優解。進退法計算步驟如圖2 所示。

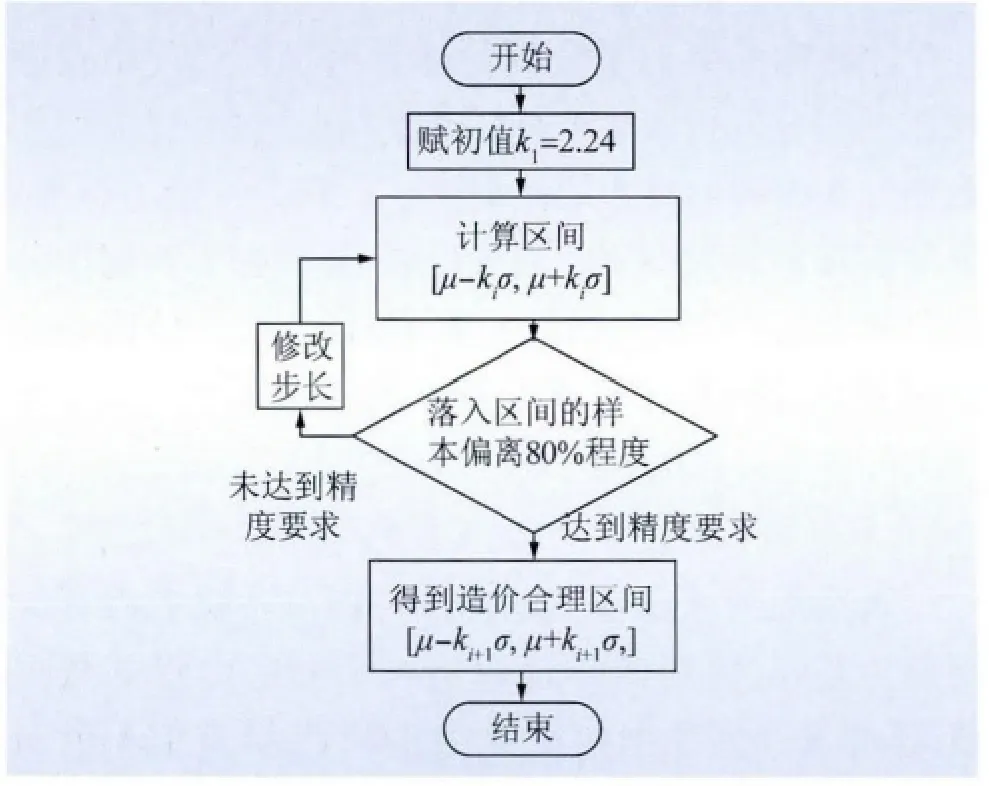
圖2 造價合理區間的系數k 值的調整計算過程Fig.2 Calculation process of k adjustment in reasonable interval

計算造價合理區間，即是計算當λ0= k 時，使得

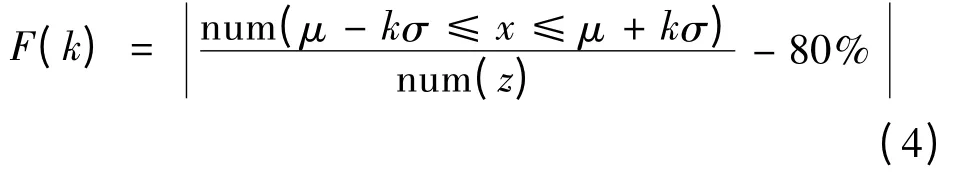
有最小值。

3 合理區間的算例分析

3.1 樣本數據

以A、B 兩個地區的35 kV 變電工程為例，做造價合理區間的算例分析，兩個地區分別有10個工程造價樣本，分別為x1i，x2i，單位為元/(kVA)，如表2所示。其中A 為中國內陸省份，B 為中國沿海省份，B 地區較A 地區經濟更為發達。

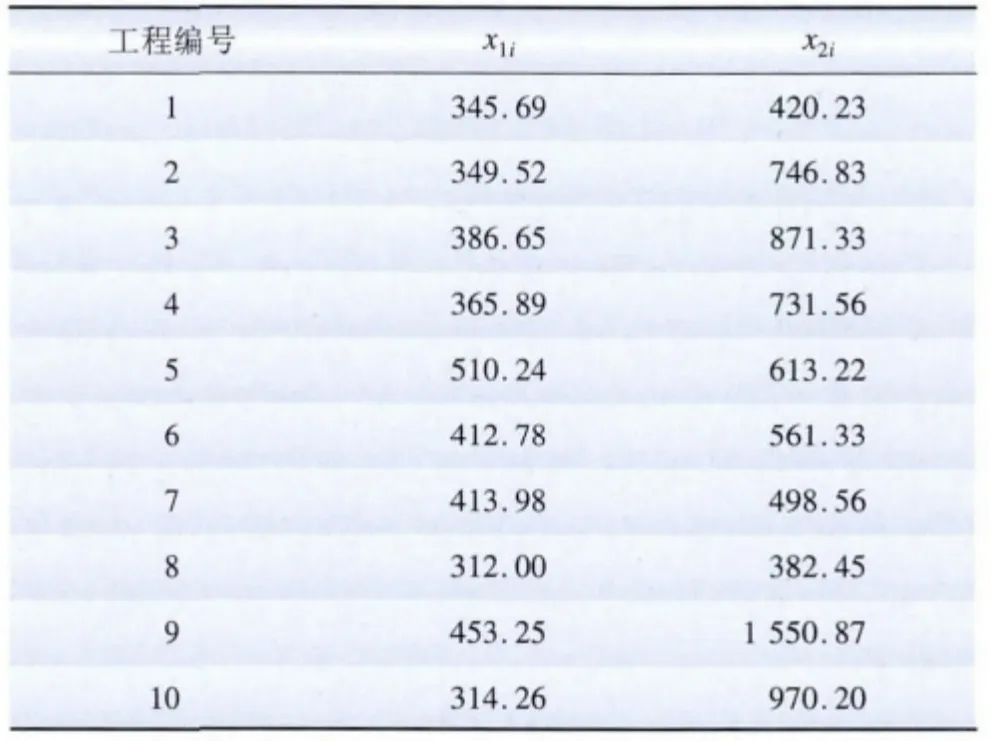
表2 某35 kV 變電工程單位造價樣本Tab.2 Unit cost sample of a 35 kV substation元/(kVA)

3.3 算例計算

計算樣本的中位數、第一四分位數、第三四分位數，分析得到樣本數據的最大值、最小值，計算樣本數據的樣本均值、樣本方差，結果如表3 所示。

計算箱線圖的上、下限，得到的結果如表4 所示。由表4 可知:x29=1 550.87 超出了上限值，不在箱線圖正常數據的范圍之內。該項工程因為建在特殊地域，項目的建設場地征用費等其他費用占總體造價的比重較高，因此拉高了總造價。如果加入合理區間的計算當中，將對計算結果起到較大的拉動作用。

對比分析剔除異常值前、后的樣本均值和樣本方差，結果如表5 所示。

表4 箱線圖上下限Tab.4 Upper and lower limit of boxplot元/(kVA)

表5 異常值的影響Tab.5 Influence of outliers

分析可知，該樣本對于樣本方差的影響達到了41.86%，對樣本方差有較大的拉動，使得計算結果偏離了合理水平。經過分析，x29屬于異常數據，應予剔除。

根據切比雪夫不等式確定初值區間，代入計算得到的樣本方差和樣本均值，得到A 地區及B 地區的初值區間φ1、φ2為

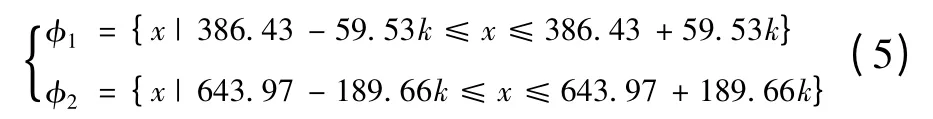
則有:

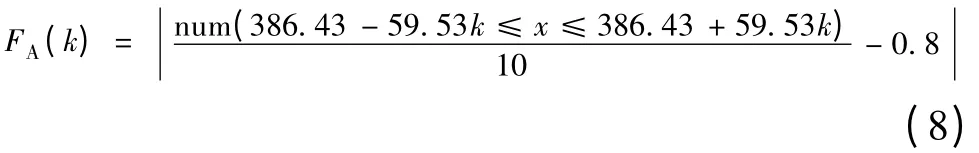
求可使FA(k)取最小值的k 值。

設初始步長h0= －0.1，ε=0.005，k0=2.24。利用進退法計算k 值，A 地區的計算結果如表6 所示。

由表6 可知，當迭代計算到16次時，步長|h| ＜ε，計算終止，得到kx1=1.215 0，計算得到造價合理區間為:φ1={x|314.10≤x≤458.76}。

同理可計算得到B 地區的計算結果如表7 所示。由表7 可知，當迭代計算到9次時，步長|h| ＜ε，計算終止，得到kx2=1.383 7，計算得到造價合理區間為:φ2={x|381.52≤x≤906.41}。

3.4 結果驗證及分析

算例計算得到的合理區間φ1、φ2分別包含了樣本A、B 中的8個樣本，占總樣本數的80%，符合論文對于合理區間的定義。

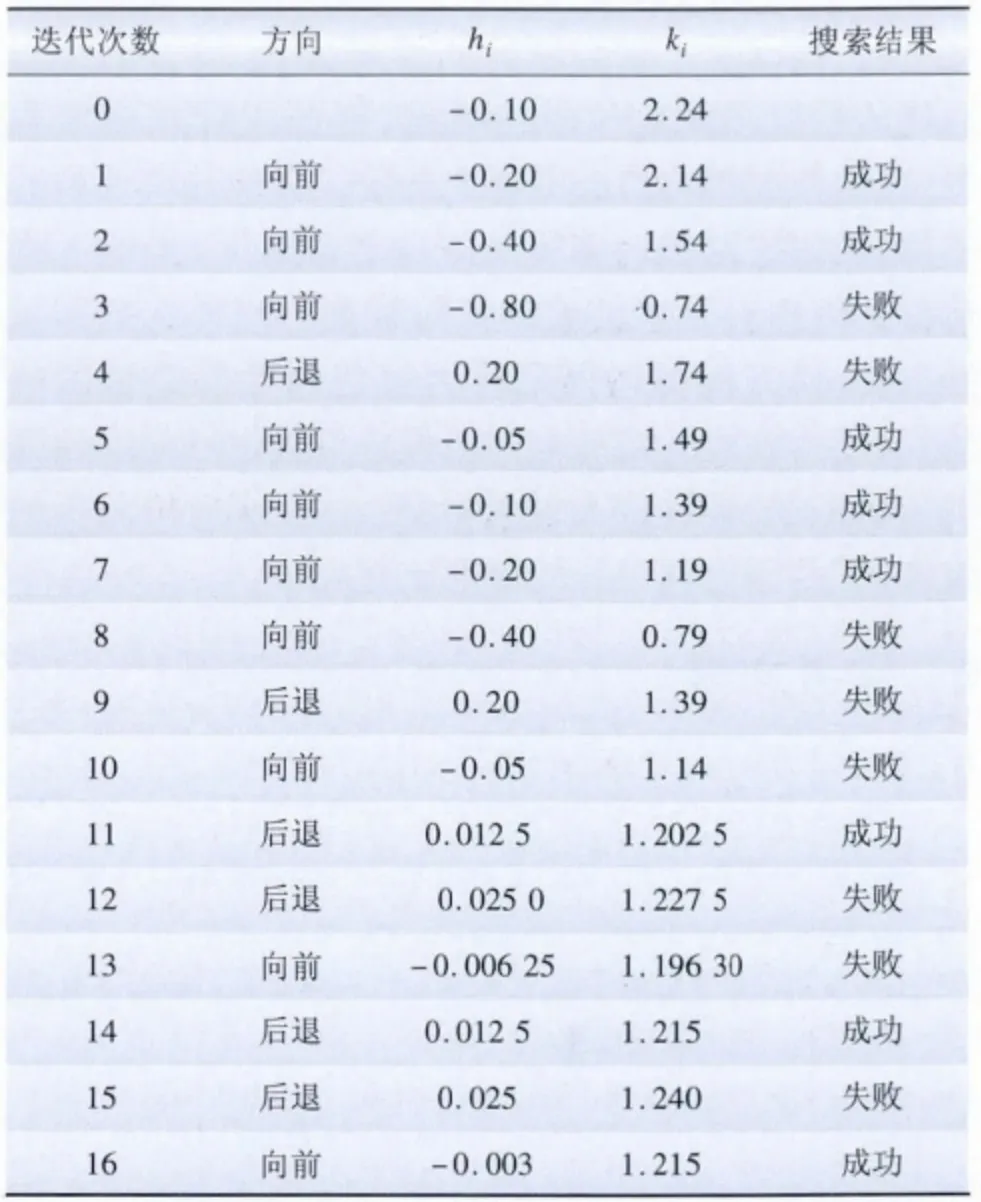
表6 A 地區參數尋優計算Tab.6 Parameter optimization calculation of Area A

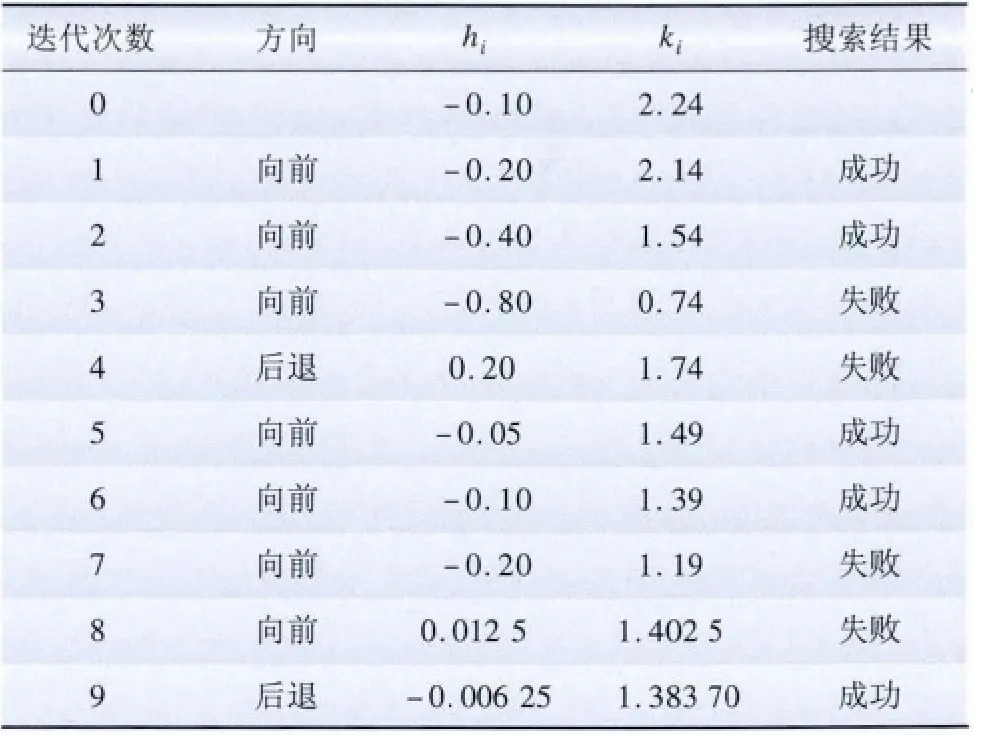
表7 B 地區參數尋優計算Tab.7 Parameter optimization calculation of Area B

由于B 地區處于沿海發達地區，線路、變電工程造價中建設場地費用占總造價的比重較大［15］，相應的造價水平也相對較高，φ2的單位容量造價水平較φ1更高一些，合理區間計算的結果也反映了這一情況。

4 結 論

在實際的工程決策、工程評審中，造價區間可以作為參考指標，用2個地區的造價合理區間的算例分析說明了論文方法的應用。本文定義了工程造價合理區間，提出了一種合理區間計算方法，該方法首先運用的箱線圖優化了原始數據，提高了計算可信程度，然后依據切比雪夫不等式確定了尋優迭代計算的初值，利用進退法計算得到造價合理區間，降低工程造價工作中對專家經驗的依賴程度。當樣本數據足夠大時，該方法可以得到較為有代表性的造價區間值，可以為該地區控制電網工程造價提供可靠度較高的分析依據，具有較大的實際意義;擴展造價分析的維度，有利于電網工程的標準化建設。

［1］李新華．對電力工程造價控制的探討［J］．電力建設，1997，18(9)，63-65．

［2］劉華敏，楊麗霞，肖紅． 電力工程造價的管理和控制［J］． 電力建設，2001，22 (3):64-66．

［3］電力規劃設計總院．電網工程限額設計控制指標(2012年水平)［R］．北京:電力規劃設計總院，2013．

［4］劉振亞．輸變電工程通用造價［M］．北京:中國電力出版社，2010:1-11．

［5］賈平俊．統計學［M］．北京:清華大學出版社，2004:95-96．

［6］史雪飛，趙彪，陳立，等.2010年輸變電工程造價分析［J］．能源技術經濟，2012，24(4):44-47．

［7］莊作傾．Box Plot-描述統計的一個簡便工具［J］． 統計與預測，2003(2):56-57．

［8］朱豐，柏又青，馮有前，等．一種針對收斂性問題的改進進退法及其仿真驗證［J］． 空軍工程大學學報:自然科學版，2010，11(2):86-90．

［9］史清錄，孔祥瑩，康健．進退法在多維非線性有約束優化問題中的應用［J］． 太原重型機械學院學報，2001，22(8):200-203．

［10］李心渝．應用經濟統計學［M］．北京:北京大學出版社，1999:67-85，88-89．

［11］GB/T 4883—2008 數據的統計處理和解釋 正態樣本異常值的判斷和處理［S］．北京:中國計劃出版社，1985．

［12］吳新元．改進割線法及其大范圍收斂性［J］．南京大學學報:自然科學版，1994，30(4):583-588．

［13］宋巨龍．利用平面上的黃金分割點法求全局最優解［J］． 數學實踐與認識，2004，34(11):113-117．

［14］程遠楚．水輪機瞬變過程計算的改進拋物線插值法［J］． 水電站設計，1997，13(1):57-61．

［15］鄭燕，宋毅．線路工程建設場地征用與清理情況現狀分析［J］． 電力技術，2010，19(7):50-52．