可數余定向極大集的若干性質

占詩源，姜廣浩

（淮北師范大學數學科學學院，安徽淮北235000）

1977年，Hutton[1]給出了極小族的概念（以下稱為Hutton意義下的極小族），并得到完備格L中的所有元都存在極小族.1984年，王國俊[2]指出這種極小族的存在性不能推出完全分配律；1985年，他繼而在文獻[3]中引入了一個稍強極小集和對偶極大集的概念，并證明了它的存在性及它和完全分配律的等價性；1986年，他在文獻[4]中構造出了更加廣泛的φ-極小集概念及其對偶φ-極大集概念.這些結果對進一步研究余定向極大集起到了重要作用.關于完備格上的極小族、極大族和完全分配格的相關理論可參見文獻[5-7].本文基于對偶可數連續格對可數余定向極大集進行研究，進而討論對偶可數連續格的一些內部刻畫，獲得了對偶可數連續格構成完全分配格的一個充分條件，并探究了完全分配格的若干個內部刻畫.

1 預備知識

定義1 設L是一個完備格，D?L，如果對于D中的任意一個可數集E?D，有d∈D，使得對于任意e∈E，d≤e，則稱D是一個可數余定向集，即D關于可數集E是余定向的.記De（L）為L中所有可數余定向子集所構成的集合.

定義2 設L是一個完備格，a、b∈L.如果對于L中任意一個可數余定向集D，inf D≤a，存在m∈D，使得m≤b，則稱a對偶可數way-below b，記作a?eb.

定義3 設L是一個完備格，若對于任意a∈L，a=inf{b∈L│a?eb}，則稱L是一個對偶可數連續格.?a∈L，記?a={x∈L│a?ex}，上集↑a={x∈L│a≤x}.若?a∈L，a=inf?a，則?e稱為對偶可數逼近的.

定義4設a∈L，F∈De（L），F稱為a的可數余定向極大集，如果滿足

（1）inf F=a；

（2）當D∈De（L）且inf D≤a時，?b∈F，存在d∈D，使得d≤b.

如果a有可數余定向極大集，則a一定有最大可數余定向極大集，記為γ（a）.

由定義3和定義4有如下命題.

命題1 設L是一個對偶可數連續格，則?a∈L，?a是a的最大可數余定向極大集.

注1 可數余定向極大集不一定是可數余定向集.如：任意一個可數極大族都是可數余定向極大集，而不一定均是可數余定向集.

定義5[8]完備格（L，≤，∨，∧）（簡記為L）稱作完全分配格，是指L滿足如下2個條件：

定義8[9]設L是一個完備格，a∈L.如果a=x∧y，得到a=x或a=y，則稱a為既約元.如果x∧y≤a，得到x≤a或y≤a，則稱a為素元.如果a=x∨y，得到a=x或a=y，則稱a為并既約元.如果a≤x∨y，得到a≤x或a≤y，則稱a為余素元.用IRRL、PRIMEL、M、N分別表示L的所有既約元、素元、并既約元、余素元所組成的集合.

2 主要結論

定理1 設L是一個完備格，則下面的條件是等價的：

（1）L是一個對偶可數連續格；

（2）L是一個可數余定向分配格；

（3）?a∈L，a有可數余定向極大集；

（4）在Hutton意義下，?a∈L，a有可數余定向極大集，并且L滿足第二可數余定向無限分配律.

證明 由定義3和定義7可知（1）?（2）.由定義3和定義 4可知（1）?（3）.而（3）?（4）是顯然的，下面只需要證明（4）?（3）.

在Hutton意義下，?a∈L，a有可數余定向極大集 γ（a），那么有 inf γ（a）=a.另外設 P={pi│i∈I}∈De（L），并且inf P≤a.令Q={a∨pi│i∈I}∈De（L），而所以?x∈γ（a），存在y∈Q，使得y≤x.此時就存在z∈P，使得y=a∨z，則有z≤x.那么γ（a）就是a的一個可數余定向極大集.即條件（3）成立.

定理2 設L是一個對偶可數連續格，映射f：L→De（L），a→γ（a），則有

（1）?a∈L，γ（a）是一個上集；

（2）?a∈L，γ（a）是一個可數余定向集；

（3）?a、b∈L并且a≤b，有f（b）?f（a）；

（4）?a∈L，{ai│i∈I}∈De（L），有

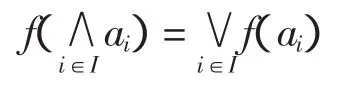
證明 （1）設 m∈γ（a），則存在 n∈↑γ（a），使得n≤m并且inf（↑γ（a））=a.?D∈De（L），inf D≤a，由γ（a）的定義可知，存在q∈D，使得 q≤n，則有q≤n≤m，所以↑γ（a）是a的一個可數余定向極大集.因為γ（a）是a的最大可數余定向極大集，故γ（a）?↑γ（a）.即有 m∈↑γ（a），所以 γ（a）是一個上集.

（2）由定義4易得.

（3）?a，b∈L，并且a≤b，設T=f（a）∪f（b），那么有

inf T=inf f（a）∧inf f（b）=a∧b=a

?D∈De（L），inf D≤a，?x∈T，如果x∈f（a），那么存在y∈D，使得y≤x；如果x∈f（b），inf D≤a≤b，那么存在z∈D，使得z≤x.綜上可知，T是a的一個可數余定向極大集，則有T?f（a）.即有f（a）∪f（b），所以有f（b）?f（a）.

命題2 設L是一個對偶可數連續格，則?a∈L，a=inf（↑a∩IRRL）.

證明 由定義8直接可得.

定理3 設L是一個可數連續格，且是一個對偶可數連續格，A?L且a∈L.如果A是a的可數余定向極大集，則↑A∩IRRL也是a的可數余定向極大集.

證明 （1）證明a=inf（↑A∩IRRL）.由于a=inf A=inf↑A≤inf（↑A∩IRRL），因此只需要證明inf（↑A∩IRRL）≤a.由命題2可知?x∈↑A，有x=inf（↑x∩IRRL）.又↑x?↑A，因此inf（↑A∩IRRL）≤x.故有

inf（↑A∩IRRL）≤inf↑A=a

綜上有 a=inf（↑A∩IRRL）.

（2）設U是一個可數余定向集，并且inf U≤a.由于?x∈↑A∩IRRL，存在y≤A，使得y≤x，因此由A是a的可數余定向極大集，可知存在z∈U，使得z≤y≤x.

綜合（1）和（2）可知↑A∩IRRL是 a的可數余定向極大集.

定理4 設L是一個可數連續格，且是一個對偶可數連續格，則?a∈L，?a∩IRRL是a的一個可數余定向極大集.

證明 由于?a∈L，?a是a的一個可數余定向極大集，并且還是一個上集，因此由定理3可得?a∈L，?a∩IRRL是a的可數余定向極大集.

注2 一般情況下，定理4中的IRRL不能用PRIMEI替代.如：若L是一個由五邊形構成的完備格，那么L就是一個可數連續格且是一個對偶可數連續格，假設 b＜a且 a、b?{0，1}，則?b∩PRIMEI={a，1}，這顯然不是b的可數余定向極大集.

定理5 設L是一個對偶可數連續格，映射f：L→De（L），a→γ（a），則

?a、b∈L，f（a∧b）=f（a）∪f（b）?L為一個鏈

證明 “?”如果L為一個鏈，那么?a、b∈L，{a，b}是可數余定向集，所以由定理2可知，f（a∧b）=f（a）∪f（b）.

“?”設?a、b∈L，均有f（a∧b）=f（a）∪f（b）.下面證明a≤b或者b≤a.對于?a、b∈L，假設a與b是不可比的，那么f（a）與f（b）一定是互不包含的.即存在m、n，使得m∈f（a）但m?f（a）且n∈f（b）但n?f（a）.因為f（a∧b）是一個可數余定向集，所以m∧n∈f（a∧b）=f（a）∪f（b），那么有m∧n∈f（a），或者m∧n∈f（b），矛盾.所以a與b是可比的.故L為一個鏈.

推論 設L是一個對偶可數連續格，映射f:L→De（L），a→γ（a），如果?a、b∈L，f（a∧b）=f（a）∪f（b）總成立，那么L是完全分配格.

定理6 設L是一個完備格，則下面的條件是等價的：

（1）L是一個完全分配格；

（2）?a∈L，?a∩IRRL是a的一個可數余定向極大集，并且L是可分配的；

（3）?a∈L，?a∩PRIMEL是a的一個可數余定向極大集；

（4）?a∈L，?a∩PRIMEL是a的可數極大族；

（5）?a∈L，?a∩IRRL是a的可數極大族.

證明 由定理 4可得（1）?（2）.（2）?（3）是顯然的.由文獻[3]的定理 2.4可類似證得（4）?（1）和（5）?（1），從而可得（4）?（5）.所以現只需證明（3）?（4）.

若（3）成立，則有 a=inf（?a∩PRIMEL）.令 S?L且inf S≤a.若T是由S的所有有限子集組成的集合，且F={inf B│B∈T}，那么S?F且inf S=inf F≤a，則F是一個可數余定向集.由（3）可得，?x∈?a∩PRIMEL，存在 y∈F，使得 y≤x.因此存在 y1，y2，…，yn-1，yn∈S，使得所以由 x∈PRIMEL 可知，存在yi，使得yi≤x.綜上知?a∩PRIMEL是a的可數極大族.

[1] HUTTON B.Uniformities on fuzzy topological spaces[J].J Math Anal Appl，1977，94（58）：559-571.

[2] 王國俊.論Fuzzy格之構造[J].科學通報，1984，29（17）：1083-1084.

[3] 王國俊.完全分配格上的點式拓撲（1）[J].陜西師范大學學報：自然科學版，1985，13（1）：1-17.

[4] 王國俊.φ-極小集及其應用[J].科學通報，1986，31（14）：1049-1053.

[5] 劉旺金，伊良忠.完全分配格中極小族、極大族的刻畫[J].數學學報，1990，33（3）：365-373.

[6] GIERZG.Continuous lattices and domains[M].Cambridge：Cambridge University Press，2003.

[7] 姚衛，李海洋.完全分配格[J].紡織高校基礎科學學報，2013，26（1）：1-9.

[8] 劉龍章，楊志輝，段龍松.關于定向極小集若干結果[J].科技通報，2007，23（5）：626-628.

[9] 史福貴.定向極小集及其應用[J].數學雜志，1993，13（4）：519-524.