SSG模型在壓縮拐角激波/湍流邊界層干擾模擬中的應用

張常賢，閆文輝，徐晶磊

(1.中航空天發動機研究院基礎研究中心，北京100028；2.中國航空研究院，北京100012；3.北京航空航天大學能源與動力工程學院，北京100191)

SSG模型在壓縮拐角激波/湍流邊界層干擾模擬中的應用

張常賢1，閆文輝2，徐晶磊3

(1.中航空天發動機研究院基礎研究中心，北京100028；2.中國航空研究院，北京100012；3.北京航空航天大學能源與動力工程學院，北京100191)

采用非線性方案模化雷諾應力再分配項的二階矩雷諾應力輸運模型——SSG模型和兩方程線性渦粘模型SST模型，對24°高雷諾數二維壓縮拐角激波/湍流邊界層相互干擾流動進行數值模擬。通過在壁面壓力分布、壁面摩擦阻力系數分布、截面速度分布及分離區大小等方面與實驗數據比較，綜合評估了上述兩種模型模擬該問題的能力。結果表明：兩種湍流模型在上述各方面都取得了與實驗較為一致的結果，但相比較而言，除SST模型在流動再附后對壁面摩擦阻力系數分布的模擬更接近實驗值外，SSG模型結果在上述其他方面均更接近實驗值。本文工作為壓縮拐角激波/湍流邊界層干擾這類流動數值模擬的湍流模型選擇提供了參考。

SSG模型；SST模型；壓縮拐角；激波；湍流邊界層；壓力應變關系

1 引言

在諸多形式的湍流模型中，雷諾應力輸運模型不同于渦粘湍流模型，其直接對湍流脈動應力建立微分形式的輸運方程并模化求解，能更真實地反映湍流機理。其中，壓力應變項Πij的存在是雷諾應力模型最顯著的特點。該項影響湍動能再分配但不會產生脈動能量，因此又稱為雷諾應力再分配項。由于該項在確定復雜湍流結構方面起著關鍵作用，故對其合理模化是保證二階矩雷諾應力模型準確預測的基礎[1]。Rotta[2]、Launder等[3]先后對Πij進行了模化研究，開發了采用線性方案的LRR-IP模式[4]。該模式后來成為雷諾應力輸運方程基準模式。后續研究中，Lumley[5]證明了采用非線性形式的必要性，推導了基于各向同性張量性質的雷諾應力輸運方程，其再分配項包含了二次項的形式，在高雷諾數和低各向異性條件下可降為LRR-IP模式。1992年，Spe?ziale等在非線性形式的基礎上發展了SSG模型[1]。此模型基于張量不變量的函數性質，同時充分考慮均勻湍流的連續性特點，以一階泰勒級數展開的形式，結合量級分析對再分配項的常系數做替換得到。Abid[6]、Jakirlic[7]、于意奇[8]和仇璐珂[9]等采用SSG湍流模型，數值模擬了凸包流動、翼型繞流、葉柵內流和內通道冷卻流等，所得結果與實驗吻合較好。

壓縮拐角激波/湍流邊界層干擾現象普遍存在于氣體的高速流動中。如當飛行器處于超聲速飛行狀態時，在飛行器進氣道口，壓氣機葉片與輪轂交界，以及飛行器外表面的機翼、機身舵面上，都存在著這種流動現象。在壓縮拐角流動中，來流面對的拐角擠壓結構誘導激波產生，接著激波與湍流邊界層相互作用破壞了流動平衡狀態而在拐角處產生分離等復雜流動現象。該問題涉及到湍流的逆壓流動、非平衡狀態、分離流動、旋轉等一系列復雜情況，是理想的驗證算例，常被用來檢驗可壓縮湍流模型的綜合預測能力。目前，國外很多相關的研究者已針對此類問題做了比較細致的研究。Settles[10～13]等在普林斯頓大學高雷諾數超聲速風洞，研究了多角度高雷諾數壓縮拐角干擾流動在激波湍流邊界層相互干擾作用下，所呈現的從附著、產生分離到產生顯著分離等多種流動形態。Elfstrom[14]、Fernholz[15]和Zheltovodov[16]等也都進行了大量相關實驗，為研究壓縮拐角流動提供了豐富的數據依據。針對這類問題的數值模擬研究已經開展，并在飛行器設計過程中起到越來越重要的作用。如何選用湍流模型能給出較為精確的數值預測，將對后續的飛行器設計研究具有重要意義。

本文采用SSG模型進行壓縮拐角激波/湍流邊界層干擾流動數值模擬。為了考察其與傳統湍流模型的區別，還選用渦粘模式的兩方程模型——SST模型[17]一同進行數值模擬，對比分析兩種湍流模型在壓縮拐角激波/湍流邊界層干擾流動中，在壁面壓力分布、壁面摩擦阻力系數分布、截面速度分布及分離區大小等方面體現出的各自特性。

2 控制方程及數值方法

2.1 控制方程

基本控制方程為可壓縮Favre平均N-S方程，其守恒形式為：

2.2 SSG模型

壓力應變項一般可表達成快速項與慢速項之和的形式，但經一系列數學變換[1]，其二次方形式在平板均勻湍流的情況下可寫成式(9)的形式。

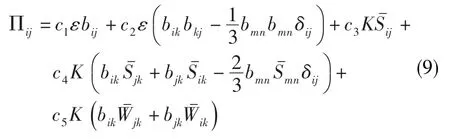
考慮到均勻湍流流動中各種情形下的漸近連續性及湍流脈動各向異性的特點，Speziale等在保留壓力應變項原有形式的同時，將Aij和Mijkl寫成以bij為變量的泰勒級數展開的形式并保留第一階導數。具體方法是將c3用替代，c1用替代。則式(9)修改之后的形式為：

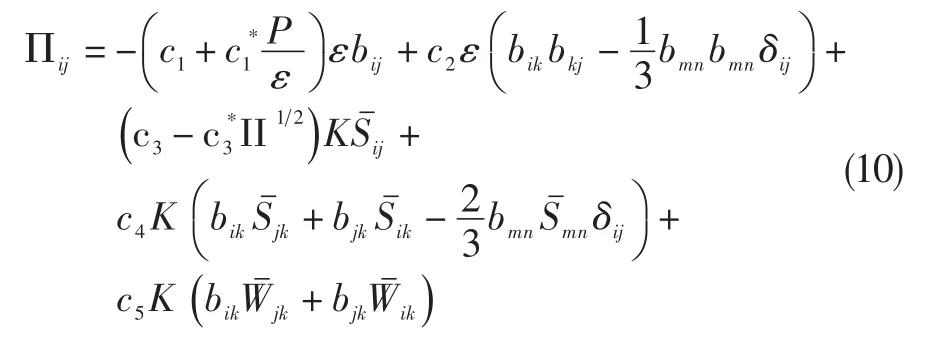
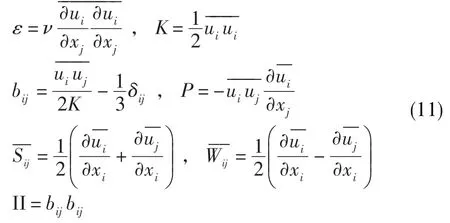
2.3 計算方法

本文所使用的計算程序為自編程序，采用有限體積法對可壓縮Favre平均N-S方程和湍流模型輸運方程進行離散求解，湍流模型分別選用SSG模型和SST模型。為提高激波位置捕捉精度，無粘通量離散采用矢通量分裂Roe[18]格式。為獲得高階的Roe格式，單元界面的流動參數由三階MUSCL插值公式構造[19，20]。為抑制激波附近解的過沖或膨脹現象，采用minmod限制器。粘性通量采用中心差分格式。時間離散采用Jameson五步Runge-Kutta顯式時間推進格式。

3 計算結果及分析

3.1 模型建立

采用Settles等在普林斯頓大學超聲速風洞進行的二維24°壓縮拐角實驗為算例進行數值模擬[10～13]。該實驗在其一系列壓縮拐角實驗中拐角角度最大，流動現象最為豐富。

實驗條件：來流馬赫數Ma∞=2.84，總溫T0=262 K，壁溫Tw=276 K，總壓p0=6.89×105Pa，特征邊界層厚度δ=23 mm，基于單位長度的來流雷諾數Re=6.3× 107。分別針對網格數為130×80、180×110、170×160和230×180進行了網格無關解驗證，其中后面三種網格所得數值模擬結果基本一致，而第一種網格的結果有些差距。因此下面計算結果均基于180×110網格。此時最底層網格法向尺寸為2.0×10-7m，可保證y+＜1。本算例中，超聲速氣流流到拐角處由于斜坡壓縮作用產生系列壓縮波并匯集為激波。激波后邊界層變厚，速度降低，逆壓梯度增加。另外，由于拐角角度過大，流動在激波后產生分離。在超聲速流動區，流場信息無法向上游傳遞。在邊界層內亞聲速流動區，激波后的大逆壓梯度向上游反饋信息，增加激波前壓強并引起邊界層厚度增加，最終迫使激波前移至新的位置形成平衡。流體在繞過分離區后再附，并繼續向前流動，形成新的壓縮波區。流動示意圖如圖1所示。

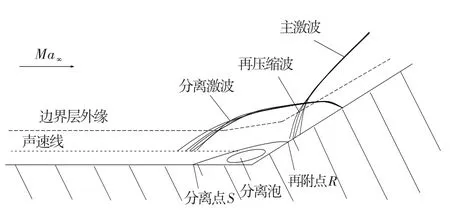
圖1 壓縮拐角激波/湍流邊界層干擾流動模型Fig.1 The scheme of shock wave/turbulence boundary layer interaction

3.2 結果及分析

壓縮拐角激波/湍流邊界層干擾問題，主要關注分離和再附位置、分離區長度、激波位置、壁面摩擦力及截面速度分布。下面結合文獻[9]中實驗數據，對SSG模型與SST模型計算結果進行評測。

3.2.1 分離區

兩種模型都模擬出了流動分離現象，具體流動分離及再附點位置見表1。可見，兩種模型都成功預測出了流動分離，都對壓縮拐角問題具有一定的模擬能力，但對分離與再附點的預測差別較大。SSG模型較為準確地預測了分離點的位置，而SST模型預測的偏差較大，分離點提前了近一倍；對再附點位置的預測，與實驗值相比，SSG模型的有所提前，而SST模型預測結果嚴重滯后。

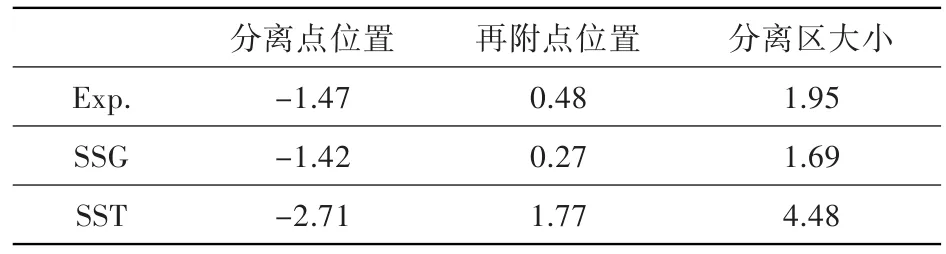
表1 分離位置區及分離區長度Table 1 Separation locations and length

圖2描繪了兩種模型所預測的分離區附近的流線圖。從分離區范圍看，SSG模型所預測的更接近實驗測量，而SST模型預測結果大于實驗測量值。總體而言，雖然兩者預測的結果都與實驗值有一定差距，但SSG模型的預測結果明顯優于SST模型。

3.2.2 壁面壓力分布

圖3示出了計算所得壁面壓力分布與實驗值的對比情況，其中零點對應位置為拐角點處。可見，SSG模型模擬結果較為準確，無論是激波開始位置還是拐角處的壓力分布曲線，都與實驗測量結果吻合較好，不足之處在于對拐角斜面末端的預測略低于實驗值。相比之下，SST模型的表現不夠理想，計算所得激波位置過于靠前，而拐角之后的壓力分布整體偏低。其原因是：算例中SST模型對湍流粘性的預計不足，造成流動過早分離，激波位置靠前和過遲再附，并伴隨壓力恢復不足。

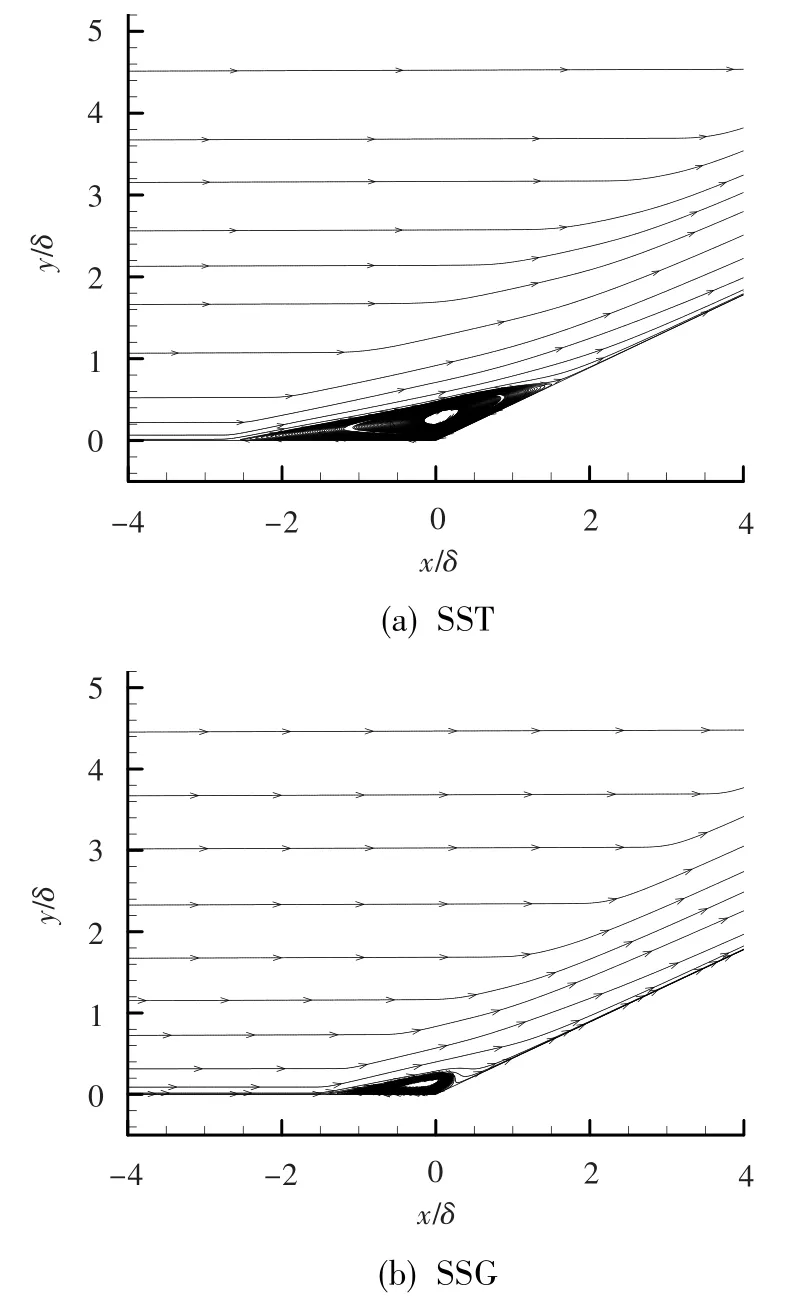
圖2 流場分離區流線圖Fig.2 Stream-trace patterns at the separation zone

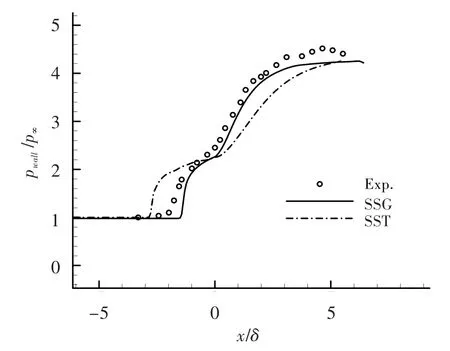
圖3 壁面壓力Fig.3 Surface pressure distribution

3.2.3 流向截面速度分布

圖4示出了沿流向截面的速度分布。可見，x/δ0=-3.012位于分離之前，兩個模型都得到了較好結果；但隨著流動的發展，SST由于對湍流粘性預測不足，出現過早分離。從位置2開始，SST所預測截面速度型與實驗出現偏差。直到位置5速度型在外緣部分開始與實驗值相比之前吻合良好。SSG的預測結果明顯優于SST的預測結果，但在拐角前相比實驗仍有一定差距。原因為雷諾應力預測偏大，這也正是其速度型明顯要比實驗值更飽滿的原因，特別是在邊界層中部尤為明顯。由于拐角后面的速度型對應的都是實驗再附后的位置，此時SSG的分離也已經結束，因此又得到了較好結果。相比之下，SST在拐角后和在拐角前的問題一樣，對湍流粘性的預測不足。對于拐角后的第一個測量點，實驗中流動已經再附，而SST還處于流動分離狀態，這直接影響了其預測準確性。從后續測量點的比較中可以看到，SST所預測的速度型在靠近壁面處相比實驗測量虧損較大。

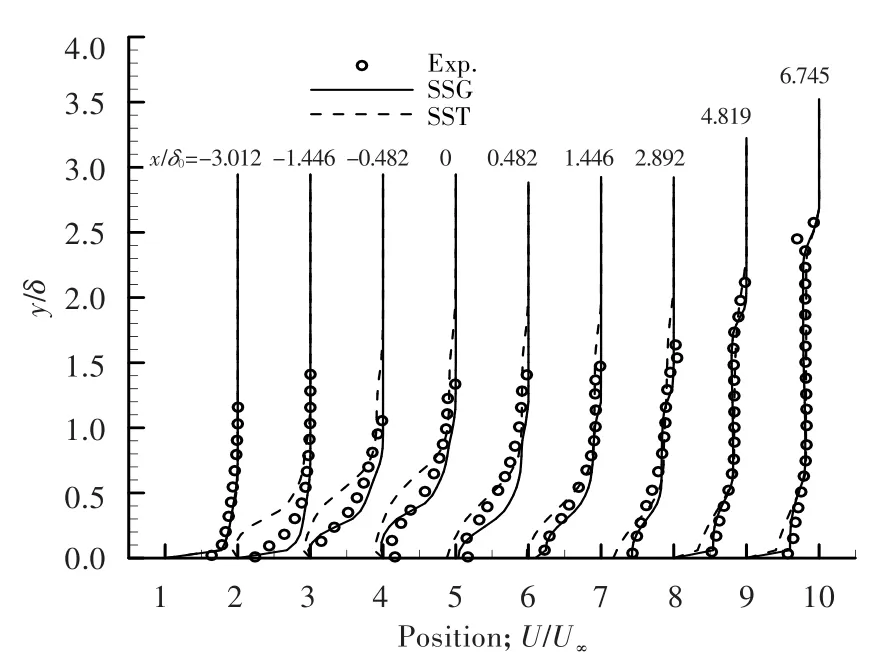
圖4 沿流向截面的速度分布Fig.4 Streamwise velocity profiles at different stations

3.2.4 壁面摩擦阻力系數分布

壁面摩擦阻力是體現湍流模型預測能力的一個重要參數。兩種湍流模型在對壁面摩擦阻力系數分布預測中的表現如圖5所示。可見，對于拐角前摩擦阻力系數開始減小的位置，SSG模型預測結果比實驗值稍為滯后，而SST模型比實驗值提前且差距稍大。在分離區內，SSG模型率先達到最小值并開始回升，其具體位置也與實驗值一致；而SST模型卻繼續降低到一個更小的數值，其直接影響就是對再附點位置的預測產生較大誤差。再附后的流動中，SSG模型迅速增加并超過實驗值，且隨著流動的發展這種差距越來越大。SST模型的再附位置更靠后，且一直保持小于實驗值發展，但更為接近實驗值。綜合看，在摩擦阻力系數的預測中，兩種模型各有優缺點，流動再附前SSG表現較好，再附后則相反。

4 結論

SST模型與SSG模型，都能成功模擬出高雷諾數二維壓縮拐角激波/湍流邊界層相互干擾流動中的流動分離與再附等現象。但相比較而言，除SST模型在流動再附后對壁面摩擦阻力系數分布的模擬更接近實驗值外，SSG模型結果在其他方面均更接近實驗值，更適應于此類型流動。具體為：

(1)SSG模型和SST模型都成功預測了流動分離。SSG模型很好地預測出分離位置，但對于再附位置則有輕微提前；SST模型由于對湍流粘性預測不足致使分離位置提前，分離區過大，再附點嚴重滯后，預測結果不理想。

(2)SSG模型預測的激波位置與實驗結果基本吻合，SST模型預測的激波位置由于流動分離則明顯提前。

(3)SSG模型較好地預測出各截面處速度型，特別是在拐角后預測結果與實驗值吻合得更好。而SST模型的預測速度型在拐角前相比實驗結果較為虧損，到流動再附后才有所好轉，虧損區域只集中在靠近壁面的區域，在邊界層外緣符合較好。出現該現象的原因是由于SST模型對湍流粘性預測不足。

(4)兩個模型對壁面摩擦阻力系數的預測都沒有得到很準確的結果。SSG模型對流動再附后的摩擦阻力系數預測結果與實驗值相差很大；SST模型在流動再附后一段位置較SSG模型預測結果更接近實驗值，但在其他區域表現較差。

[1]Speziale C G，Sarkar S，Gatski T B.Modeling the Pres?sure-Strain Correlation of Turbulence:An Invariant Dy? namical Systems Approach[J].Journal of Fluid Mechanics，1991，227：245—272.

[2]Rotta J C.Statistische Theorie Nichthomogener Turbulenz [J].Z.Phys，1951，129(6)：547—572.

[3]Launder B E，Reece G，Rodi W.Progress in the Develop?ment of a Reynolds Stress Turbulence Closure[J].Journal of Fluid Mechanics，1975，68：537—566.

[4]張兆順，崔桂香，許春曉.湍流理論與模擬[M].北京：清華大學出版社，2005.

[5]Lumley J L.Turbulence Modeling[J].Journal of Applied Mechanics，1983，50(4b)：1097—1104.

[6]Abid R，Morrison J H，Gatski T B，et al.Prediction of Aerodynamic Flows with a New Explicit Algebraic Stress Model[J].AIAA Journal，1996，34(12)：2632—2635.

[7]Jakirlic S，Eisfeld B，Jester-Zürker R，et al.Near-Wall, Reynolds-Stress Model Calculations of Transonic Flow Configurations Relevant to Aircraft Aerodynamics[J].Inter?national Journal of Heat and Fluid Flow，2007，28(4)：602—615.

[8]于意奇，顧漢洋，楊燕華，等.稠密柵元不同子通道內湍流流動的RANS和URANS模擬[J].原子能科學技術，2011，45(10)：1191—1197.

[9]仇璐珂，王新軍，韓宇萌，等.蛇型冷卻通道中的蒸汽流動與換熱特性研究[J].空氣動力學學報，2011，29(2)：235—239.

[10]Settles G S，Vas I E，Bogdonoff S M.Details of a Shock-Separated Turbulent Boundary Layer at a Compres?sion Corner[J].AIAA Journal，1976，14(12)：1709—1715.

[11]Settles G S，Fitzpatrick T J，Bogdonoff S M.Detailed Study of Attached and Separated Compression Corner Flowfields in High Reynolds Number Supersonic Flow[J].AIAA Jour?nal，1979，17(6)：579—585.

[12]Settles G S.An Experimental Study of Compressible Tur?bulent Boundary Layer Separation at High Reynolds Num?ber[D].Princeton：Princeton University，1975.

[13]Settles G S，Dodson L J.Hypersonic Shock/Boundary-Lay?er Interaction Database[R].NASA CR-177577，1991.

[14]Elfstrom G M.Heat Transfer from Hypersonic Turbulent Flow at a Wedge Compression Corner[J].Journal of Fluid Mechanics，1972，53(1)：113—127.

[15]Fernholz H H，Finley P J，Dussauge J P，et al.A Survey of Measurements and Measuring Techniques in Rapidly Dis?tortedCompressibleTurbulentBoundaryLayers[R]. AGARDograph 315，1989.

[16]Zheltovodov A A，Trofimov V M，Schuelein E，et al.An Ex?perimental Documentation of Supersonic Turbulent Flows in the Vicinity of Sloping Forward-and Backward-Facing Ramps[R].USSR：Institute of Theoretical and Applied Me--chanics，USSR Academy of Sciences，1990.

[17]Wilcox D C.Reassessment of the Scale Determining Equa?tion for Advanced Turbulence Models[J].AIAA Journal，1988，26(11)：1299—1310.

[18]Roe P L.Approximate Riemann Solvers,Parameter Vec?tors,and Difference Schemes[J].Journal of Computational Physics，1981，43(2)：357—372.

[19]Van Leer B.Towards the Ultimate Conservative Difference Scheme V:A Second Order Sequel to Godunov’s Method [J].Journal of Computational Physics，1979，32：101—136.

[20]Anderson W K，Thomas J L.Comparison of Finite Volume Flux Vector Splitting for the Euler Equation[J].AIAA Jour?nal，1986，24(9)：1453—1460.

Application of SSG Model to Shock-Wave/Turbulent Boundary-Layer Interaction Flow at a Compression Corner

ZHANG Chang-xian1，YAN Wen-hui2，XU Jing-lei3
(1.China Aerospace Engine Establishment，Beijing 100028，China；2.Chinese Aeronautical Establishment，Beijing 100012，China；3.School of Energy and Power Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100091，China)

Numerical investigations on shock-wave/turbulent boundary-layer interaction flow at compres?sion corner were carried out using both SSG model and SST model.The results were compared with experi?ment data,including the pressure distribution,friction coefficients on the wall and velocity profiles at differ?ent positions,in order to evaluate which model was better.The results indicate that the SSG model gives a better performance for compression corner compared with SST model,but the simulation results of friction coefficient on the wall by SST model is closer to the experiment data.This investigation is referential to choose the turbulence model simulating shock-wave/turbulent boundary layer interaction flow.

SSG model；SST model；compression corner；shockwave；turbulent boundary layers；pressure-strain correlation

V211.3

：A

：1672-2620(2014)03-0001-05

2013-10-16；

：2014-06-02

張常賢(1981-)，男，江蘇豐縣人，工程師，博士，主要從事湍流模型數值研究。