基于最優閾值小波包分析的轉子振動信號降噪研究

趙凱，李本威，徐圣田

(1.海軍航空工程學院飛行器工程系，山東煙臺264001；2.92635部隊，山東青島266300)

基于最優閾值小波包分析的轉子振動信號降噪研究

趙凱1，李本威1，徐圣田2

(1.海軍航空工程學院飛行器工程系，山東煙臺264001；2.92635部隊，山東青島266300)

針對采集轉子振動信號時信號中往往夾雜著噪聲干擾的問題，提出了一種自尋優閾值的小波包降噪方法。該方法可對不同振動信號自尋優地設置閾值，且閾值的選取與所研究的信號有關而與信號長度無關；并根據采樣定理計算不同轉子轉速對應的小波包分解的最低層數。對多種信號進行的降噪研究表明，該方法可有效降低轉子振動信號中的噪聲干擾。

航空發動機；轉子振動；最優閾值；小波包分析；信號降噪；閾值函數；采樣定理

1 引言

轉子是航空發動機的重要部件，在不同工況下運轉會產生不同的振動信號，通過研究振動信號可以得知轉子的運轉狀態。目前，關于轉子的研究主要是針對不同的振動信號展開各種數據挖掘研究，然后對轉子的運行狀態進行評估并預測未來發生的故障，或在故障時對其進行故障診斷等。如文獻[1]融合小波能譜熵和支持向量機的特點，提出了基于小波能譜熵的SVM故障診斷方法，實現了對未知轉子振動故障的識別；文獻[2]針對轉子的多種故障模式，提出了基于排列組合熵的SVM故障診斷方法，有效提高了轉子故障診斷的準確性。但在振動信號的采集過程中，往往會夾雜著其他信號的干擾，即噪聲。如何對振動信號去除噪聲，使振動信號能真實反映轉子的運行狀態，不僅是數據預處理工作的重要內容，也是對振動信號進行上述研究的前提和基礎。

由于發動機內部結構及工作環境非常復雜，所以其振動信號也呈現出非線性和非平穩的特性。小波分析是一種時間-頻率尺度分析方法，具有多分辨率分析的特點[3]，特別適用于分析發動機轉子振動信號這類非線性信號。而小波包作為小波概念的推廣，能提供一種更加精細的分析方法，因此小波包變換也被廣泛應用于非平穩信號處理中[4]。如文獻[5]在小波多分析閾值法的基礎上，對閾值進行了修正；文獻[6]基于混沌信號具有分形結構的特點，提出一種分數維與小波變換相結合的帶觀測噪聲混沌信號的噪聲去除新方法。小波包分析與小波分析在降噪原理上相同，所以兩者計算閾值的方法一樣。下文在沒有明確指出區別時，兩者不做區分。

本文采用最優閾值小波包降噪的方法對含噪振動信號進行研究，針對小波包分析在轉子振動信號降噪方面的兩個重要問題，即小波包分解層數和閾值的確定，進行研究并提出解決方法。

2 小波降噪

2.1 小波降噪原理

小波降噪方法認為，含噪信號的真實值與噪聲的小波系數在小波空間內有著不同的分布，對含噪信號進行小波分解后，噪聲主要集中在高頻的小波系數中，通過設置閾值可將含噪部分去除，最后對信號重構，即達到對信號降噪的目的[7]。假設有含噪的一維信號f，可表示為：

式中：s(t)為信號的真實值；n(t)是方差為δ2的高斯白噪聲，且服從高斯分布N(0,δ2)。

小波降噪的目的就是使含噪信號與信號真實值的均方根誤差δ(δ=E‖f-s‖2)最小[8]。

小波包降噪方法的步驟[9]如下：①對一維信號f進行小波包分解，首先選擇一個小波并確定其分解層數N，然后對信號進行分解；②確定最優小波包基，對于一個給定的熵標準，計算最優樹；③設定小波包分解系數的閾值；④信號的小波包重構。

上述各步中，最主要的是閾值選取。閾值選取過大或過小都會直接關系到信號降噪處理效果，所以目前大多數研究圍繞在構造合適的閾值函數上。其次是計算小波包分解層數的方法。本文根據采樣定理，計算出不同的轉速，振動信號對應的最小的小波包分解層數不同。

2.2 小波包分解層數研究

由文獻[10]可知，小波分解層數由分解后得到的最低倍頻決定。通常，轉子故障信號的頻率特征需滿足兩個條件：最低倍頻在0.5倍以下，最高倍頻在10倍以上。即：如果轉速為2 000 r/min，可知基頻為33.3 Hz，那么最低倍頻應在16.7 Hz以下，最高倍頻在333.0 Hz以上。采樣時間間隔需滿足

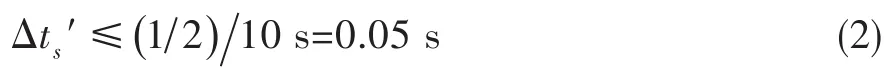
小波包分解層數m需滿足公式[10]：

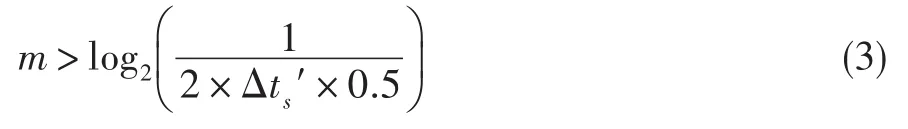
由式(3)可計算出，當Δts′=0.05 s時，m＞4.322，即分解層數要不小于5。當分解層數為5時，最低頻帶范圍為(0～15.6 Hz)。

小波包分解層數越多，劃分就越細致，得到的信息也越多，但由此帶來的計算量將呈幾何級增長。因此，實際應用中，小波包分解層數不可能無限增大，這樣就有由轉子穩定轉速確定小波包分解的最小分解層數。

2.3 閾值的選取方法

目前常用的小波降噪閾值選取方法有以下四種：固定閾值(即Sqtwolog算法)、無偏似然估計閾值(即Rigrsure算法)、啟發式閾值(即Heursure算法)和極大極小閾值(即Minimaxi算法)。

(1)固定閾值的計算公式為[11]：

式中：σ為噪聲標準差，N為信號長度。Donoho提出了估計噪聲標準差的方法[12]，即

固定閾值方法的缺點是固定閾值與信號長度相關[13](見式(4))，當信號長度趨于無窮時，高頻的小波系數就會被置為零，出現過扼殺現象，此時小波濾波器退化為低通濾波器，重構振動信號后造成信號失真。

(2)無偏似然估計原則是一種基于Stein無偏似然估計原理的自適應閾值選擇。對于一個給定閾值t，得到其似然估計，再將該估計最小化，就得到所選閾值。這種方法是一種軟件閾值估計器。

(3)啟發式閾值是一種綜合無偏似然估計準則和固定閾值的閾值選取方法，所選擇的是最優預測變量閾值。當信噪比很小、按無偏似然估計原則處理的信號去噪效果不理想時，按固定閾值的方法來確定閾值。其與軟閾值函數結合時去噪效果不錯，但與其他閾值函數結合時降噪效果可能很差[14]。

(4)極大極小閾值方法是一種固定閾值選擇形式，由Donoho基于統計學上的極大極小值原理提出。它產生一個最小均方差的極值，而不是沒誤差。

上述的閾值估計方法都不是最優，工程中應用較多的固定閾值在噪聲較多時去噪效果明顯，無偏似然估計對高頻信息保留較多，啟發式閾值與極大極小閾值在信號的高頻信息較少包含噪聲時比較有效[15]。因此需要找到針對該含噪信號的最佳閾值。

2.4 最優閾值的計算方法

目前，針對信號的小波閾值去噪算法大多集中在對閾值函數的改進上，對閾值選取的研究較少。本文在文獻[16]的基礎上，提出了基于最優閾值的小波包去噪方法。

最優閾值自尋優過程為：將閾值作為一個變量，它不隨輸入信號長度的不同而變化，但對于任意信號，閾值從0到某一終值不斷改變。輸入信號通過這樣一個自尋優過程，找出使最小的值，即最優閾值[16]。

在最優閾值自尋優過程中，當小波空間上的閾值從0增大到某一數值后，衡量去噪效果的信噪比等數值不會再隨閾值的增大而改變，則此閾值稱為高頻死去值，如圖1所示。文獻[16]對高頻死去值的存在予以了證明。

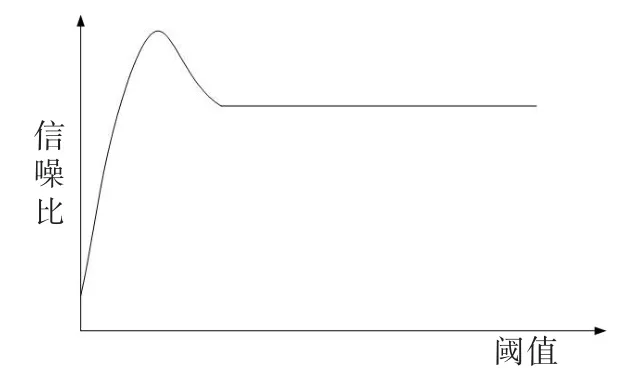
圖1 高頻死去值現象Fig.1 Dead value of high frequency phenomenon

由上可得：在某一分解層中，高頻死去值與所采用的閾值函數無關，只與信號自身相關。當閾值函數的信噪比在某一閾值之后為一定值，那么將兩個不同的閾值函數(如軟閾值函數和模平方法閾值函數)，在相同條件下對同一信號進行計算，當超過某一閾值時，如其信噪比兩兩相減為零，則該閾值即為所求的高頻死去值；或者在單一閾值函數的基礎上，編程計算在某一閾值之后，其信噪比不再變化，以確定高頻死去值的大小。高頻死去值就是最終得到的閾值。

2.5 算例

對于加入隨機產生的高斯白噪聲，當前的延拓模式是補零的信號，分別以Rigrsure、Heursure、Sqt?wolog、Minimaxi及最優閾值法為閾值算法對其進行閾值計算，結果見表1。

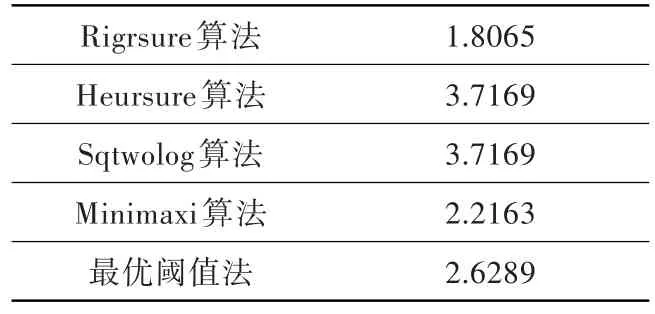
表1 各閾值算法求得的閾值Table 1 The threshold obtained by the threshold algorithms

當信號只有少量高頻系數位于噪聲范圍內時，使用Stein無偏似然估計的Rigrsure自適應閾值和極大極小值原理的Minimaxi閾值選擇方法較保守，僅將部分系數置為零，不容易丟失真實信號成分。因此在信號的高頻信息有很少一部分在噪聲范圍內時，這兩種閾值選擇規則可將弱小的信號提取出來。另外兩種閾值選擇方法可更有效地去除噪聲，但也容易將有用信號的高頻部分當作噪聲過濾掉。最優閾值算法則處于這兩者之間。文獻[16]從信噪比及均方根誤差兩方面，驗證了最優閾值算法要優于另外四種方法。

3 實驗仿真及分析

3.1 算法驗證

原始信號以Matlab程序自帶的blocks、bumps、heavy sine、doppler、quadchirp和mishmash六種信號為例，對其加入相同的高斯白噪聲，并用Rigrsure、Heursure、Sqtwolog、Minimaxi及最優閾值法為閾值算法，分別對其進行降噪處理，結果如圖2所示。可見，相比于其他四種經典方法，基于最優閾值法的小波降噪效果總體最好，對這六種不同信號的處理均有不錯表現。從本質上講，最優閾值法是對閾值取值方法的改進，是一種平衡的降噪方法。

3.2 轉子振動數據分析

數據來源于振動實驗臺采集的轉子振動信號，采用symN系列的sym8小波函數。由于轉子的轉速為2 000 r/min，所以按前文介紹的方法，對振動信號進行6層小波包分解，計算最優閾值。當加入的高斯噪聲的信噪比為20 db和50 db時，分別使用小波和小波包降噪方法對含噪信號進行降噪。圖3顯示了800個采樣點的降噪結果。可見，小波包降噪方法的效果整體上要優于小波降噪方法，且信噪比越高小波包降噪的效果越好。如圖中對第5個尖峰的恢復上，小波包的降噪效果明顯好于小波。綜上所述，基于最優閾值的小波包降噪方法，對轉子振動數據有著優良的降噪效果，具有一定的應用價值。

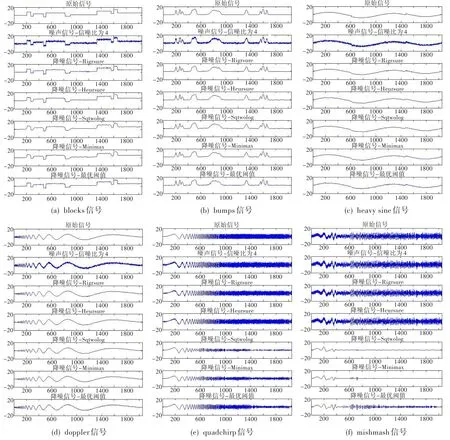
圖2 各閾值算法對六種信號的降噪效果對比Fig.2 The noise reduction effect comparison of six kinds of signal based on the threshold algorithms

4 結論

針對轉子采集振動信號時往往夾雜著噪聲干擾的問題，提出了一種自尋優閾值的小波包降噪方法。相比于傳統方法，該方法對不同振動信號設置不同閾值，即閾值與信號本身而不是信號長度有關，并根據轉子轉速求得小波包分解的最低層數。對多種不同信號降噪計算的結果表明，本文方法可有效降低噪聲影響，達到了預期效果，但仍需進一步完善：①最優小波包基的選取——這也是小波包降噪方法的難點之一；②提高最優閾值法的運行速度——因其算法復雜，運行時間較其他經典方法長。

[1]艾延廷，費成巍.轉子振動故障的小波能譜熵SVM診斷方法[J].航空動力學報，2011，26(8)：1830—1835.

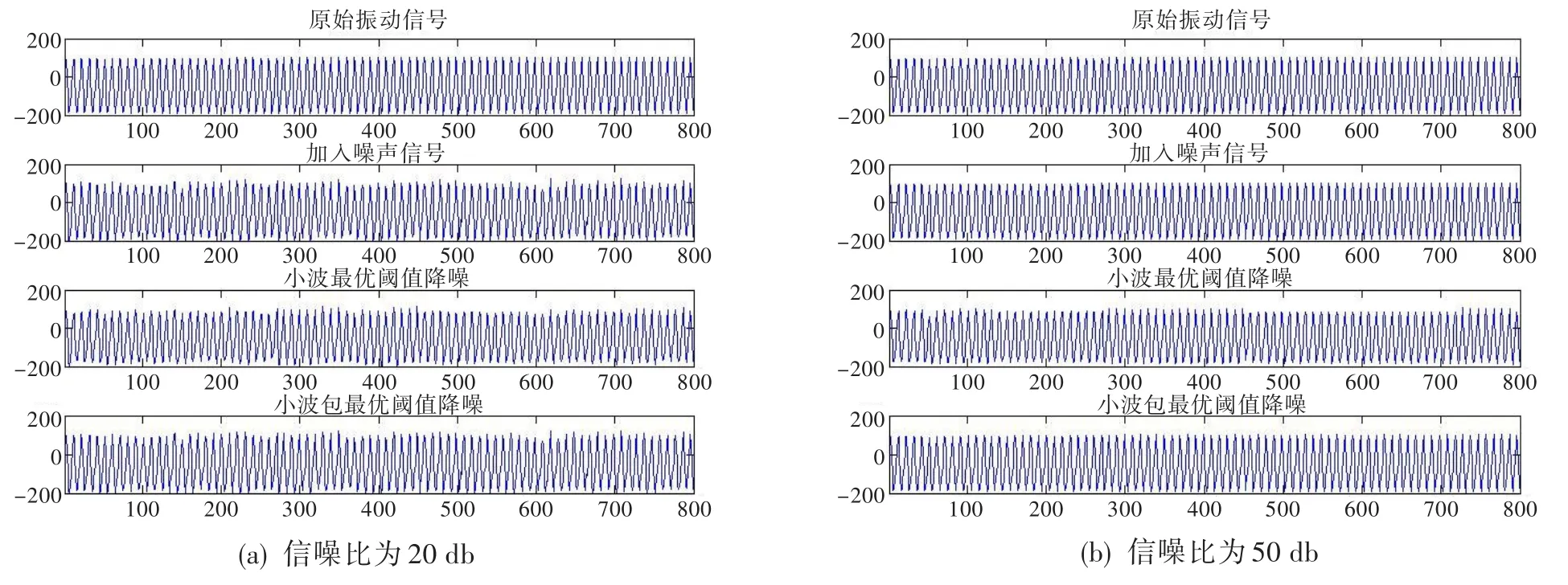
圖3 振動信號在各信噪比下的降噪效果對比Fig.3 The noise reduction effect comparison of the vibration signal under different SNRs

[2]趙凱，李本威，李冬，等.基于排列組合熵的轉子振動信號故障診斷SVM方法研究[J].燃氣渦輪試驗與研究，2013，26(3)：38—42.

[3]肖云魁，李世義，王建新，等.以粗糙集近似逼近理論提取發動機振動故障特征[J].振動、測試與診斷，2004，24 (4)：262—265.

[4]黃義仿，朱曉然，趙榮珍，等.基于小波分析和矩不變量的轉子故障量化特征提取研究[J].化工機械，2007，34 (6)：309—312.

[5]趙曉燕，李宏男.一種改進的小波分析消噪方法及其在健康監測中的應用[J].振動與沖擊，2007，26(10)：138—139.

[6]馬麗萍，石炎福，余華瑞.含噪聲混沌信號的小波去噪方法研究[J].信號處理，2002，18(1)：83—87.

[7]Donoho D L，Johnstone I M.Wavelet Shrinkage:Asymp?topia[J].Journal of the Royal Statistical Society，1995，57 (2)：301—369.

[8]Donoho D L.Unconditional Bases Are Optimal Bases for Data Compression and for Statistical Estimation[J].Ap? plied and Computational Harmonic Analysis，1993，1(1)：100—115.

[9]葛哲學，沙威.小波分析理論與MATLAB R2007實現[M].北京：電子工業出版社，2007：123—126.

[10]鄧堰，陳果.轉子故障信號的小波能量特征自動提取[J].應用科學學報，2007，25(5)：510—515.

[11]Donoho D L，Johnstone I M.Ideal Spatial Adaptation by Wavelet Shrinkage[J].Biometrika，1994，81(3)：425—455.

[12]Donoho D L.De-Noising By Soft-Thresholding[J].IEEE TransactionsonInformation Theory，1995，41(3)：613—627.

[13]楊桂芹，徐紅莉.基于最大信息熵的小波包閾值去噪語音增強算法[J].測控技術，2011，30(10)：12—17.

[14]Bruce A G.Understanding Waveshrink:Variance and Bi?as Estimation[J].Biometrika，1996，83(4)：727—745.

[15]Daubechies I.The Wavelet Transform:Time-Frequency Localization and Signal Analysis[J].IEEE 2000，36：961—1005.

[16]肖方煜，湯偉，傅娜.自尋優閾值小波去噪方法[J].信號處理，2012，28(4)：577—586.

Denoising of Rotor Vibration Signals Based on the Optimal Threshold Wavelet Packet Analysis

ZHAO Kai1，LI Ben-wei1，XU Sheng-tian2
(1.Department of Airborne Vehicle Engineering，Naval Aeronautical and Astronautical University，Yantai 264001，China；2.The 92635thUnit of PLA，Qingdao 266300，China)

Since the rotor vibration signal acquisition often mingled with the noise interference,a self-opti?mized threshold wavelet packet denoising method was proposed.Self-optimized threshold,which was linked to the signal itself rather than the length of signal,was set for different vibration signals.And the low?est layer of wavelet packet was decomposed according to the rotor speed.The research results show that, this method can reduce the noise disturbance in rotor vibration signal effectively,and has certain applica?tion value.

aero-engine；rotor vibration；the optimal threshold；wavelet packet analysis；signal denoising；threshold function；sampling theory

V235.13

：A

：1672-2620(2014)03-0022-05

2013-07-21；

：2014-05-12

國家自然科學基金青年基金(61102167)

趙凱(1983-)，男，山東煙臺人，博士研究生，研究方向為航空發動機故障診斷、測試與維護技術。