感應電機三維溫度場建模與仿真計算

王治軍，高忠峰，周茜

?

感應電機三維溫度場建模與仿真計算

王治軍1，高忠峰2，周茜2

(1. 海軍航空兵學院，河南濟源 454650；2. 91446部隊，河北涿州 072750）

本文以自行研制的5.5 kW五相異步電機為研究對象，建立了三維溫度場有限元計算模型。采用順序電磁—熱耦合方法，將電磁場分析中的節點損耗作為熱源施加到溫度場計算中，完成了對電機穩態溫度場的計算，得到了電機內部各部件的溫度分布，并以此為基礎，研究了不同溫度條件對感應電機參數和運行性能的影響。

異步電機 有限元方法 順序電磁熱耦合 溫度場 參數分析

0 引言

電機是一個涉及多物理場、強耦合的研究對象，對于某些特種電機，其應用場合特殊，工況復雜，傳統單場研究手段已不再適用，而建立涉及溫度、流體和電磁等多場耦合的電機設計和分析方法逐漸成為人們的研究熱點。

文獻[1]、[3]介紹了通過建立電機軸向剖面2維有限元模型來計算電機溫度場的方法，但沒有考慮繞組端部的溫度，軸向上溫度差異也無法體現；文獻[4-6]建立了電機定子三維有限元模型，計算了電機的穩態溫度場，但沒有作溫度對電機參數影響的討論；我國學者李偉力對電機的溫度場進行了詳細計算與分析，不過其研究對象多為大型發電機，對于應用廣泛的中小型電機未作進一步研究；文獻[8]中建立了異步電機的精確熱網絡模型，通過CFD（計算流體動力學）計算了機殼表面散熱槽內冷卻空氣的流速分布，這些研究對于電機溫度場有限元計算具有重要意義。

本文以一臺5.5 kW五相異步電機為研究對象，建立了其有限元三維模型，應用電磁和熱的順序耦合方法計算了電機穩態溫度場，得到了電機內部各部件的溫度分布，并以此為依據，比較了不同溫度條件下電機主要參數與性能指標的變化，為電機電磁和散熱的優化設計打下基礎。

1 溫度變化對異步電機參數及性能影響研究

制造電機所應用的繞組、鼠籠導條與鐵心等材料對于電能、磁能的傳導性能會隨著溫度變化而改變。從建立電機數學模型的角度來看，在不同溫度條件下，實際上是方程的參數矩陣發生了數值變化。因此，由數學模型所做的一系列推導都會發生相應變化。

下面分別從電機內部電路與磁路的參數變化來分析說明溫度升高對電機主要性能的影響。

當定子繞組溫度升高，材料電阻率增大，使繞組電阻值增大，進而增加了定子繞組的電損耗。對于鼠籠型轉子繞組，可將其等效成一個對稱多相繞組進行分析。轉子鼠籠一般使用鑄鋁或銅材，因此與定子繞組類似，其溫度升高使材料電阻率變大，最終導致轉子鼠籠上的電損耗增加。應注意到在定、轉子電損耗增加的同時，電機的效率降低，溫度則進一步升高。

由于電機正常工作時鐵心材料在近飽和狀態，過高的溫升還會引起材料飽和，改變氣隙磁場的分布波形，嚴重影響電機的工作性能。

2 有限元方法電磁場-溫度場順序耦合計算基礎

三維電場求解中以標量電位為待求量，三維電場滿足方程：

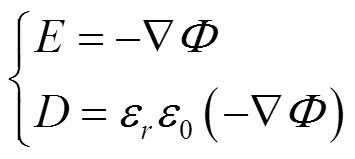
三維靜磁場的麥克斯韋方程組如式(5)所示：

對電機溫度場有限元模型有如下假設：

1）電機表面向周圍空氣的輻射換熱折算到表面的對流換熱系數；2）對流換熱系數在氣隙內部是相同的；3）定子繞組的集膚效應忽略不計；

根據以上假設，對電機計算域建立三維穩態熱傳導數學模型：

通過建立模型進行適當的網格剖分，即可實現順序電磁熱耦合有限元計算。順序耦合方式首先計算電磁場有限元模型，將計算結果中的節點損耗作為溫度場模型的初始條件，再按照上式計算求解域全部節點的溫度所成的溫度列陣。因此，為了使得節點損耗能作為中間變量在兩個方程之間有效傳遞，必須要求電磁場、溫度場有限元執行相同的網格剖分。

3 五相異步電機有限元計算模型建立

為了進一步研究溫度變化對電機性能參數的影響，本文分別建立了五相鼠籠異步電機的電磁場與溫度場有限元模型，并且進行了這兩個物理場之間的順序耦合計算，得到電機各部分溫度場分布，并以該溫度場結果為依據，考察了電機在不同溫度下的性能參數變化。電機的基本參數見表1。

3.1 異步電機電磁場有限元建模

本文所做的電磁場有限元計算為其溫度場有限元計算提供了計算依據，計算結果中的鐵耗、銅耗等作為熱載荷加載到溫度場模型中作為輸入量。

電磁場模型設置與求解計算過程不是本文重點，在此不作贅述。僅列出電機各部分的損耗計算值以作參考，見下表2。

3.2 異步電機三維溫度場有限元建模

由于電機本身結構復雜，部件繁多，如果嚴格按照實際建立模型會導致模型文件過大，占用過多計算機資源，降低計算求解速度，甚至無法執行文件。因此，將電機做了相應等效簡化。

具體做法為，不考慮集膚效應的情況下，將每相定子繞組整體簡化為單根導體，放置在定子槽中心部位。導體橫截面積與簡化之前相等。定子槽內除了各相繞組以外，還包含有導體間的絕緣浸漬漆、導體絕緣層、槽絕緣、槽楔等成分與部件。在這里將它們統一處理成一層包裹導體的等效絕緣體，填充每一個定子槽，以簡化模型，如圖1所示。為了保證等效前后其對外的熱性能保持不變，需要確定等效絕緣的導熱系數。由于電機繞組經過真空浸漆，可以認為絕緣中不存在氣隙的影響，按照熱阻串聯的概念，理論計算導熱系數使用下式(7)：

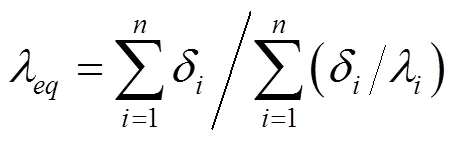
通過實驗測量來確定導熱系數能確定較為可靠的結果。事實上，由于絕緣材料形制不一，槽內導線嵌放時多次交叉接觸，等效厚度無法準確確定，這些在理論計算中難以考慮的因素會導致計算值與實際情況產生較大偏差。

另外定子繞組端部也需要做相應簡化。電機各相繞組的端部集中在一起，通過絕緣材料彼此隔開，是電機中發熱嚴重，也是散熱條件惡化的部分。現將其簡化成徑向兩層，軸向四層的結構，原則上保持等效前后的體積大致相等。圖2顯示的是定子繞組端部等效模型（無絕緣層，各相間有氣隙間隔）。

4 計算結果與分析

4.1 順序耦合溫度場計算結果

本文通過順序電磁熱耦合方法計算得到了電機的溫度場分布，通過散熱系數的設置模擬了模型加入機殼肋片與風扇等散熱措施，因此在軸向上溫度分布有明顯差異，電機各部分溫度分布如圖3-5所示。端部溫度較之槽內溫度要高，這與理論分析相符。因此在實際電機設計中，采用空氣冷卻時一般在軸向上安裝風扇，抽出或鼓入冷空氣來改善散熱條件。

電機定子溫度分布呈現入風側溫度低而出風側溫度高的規律，定子槽內散熱條件惡化，槽內溫度比定子貼近機殼一側溫度高，定子齒部溫度較高，軛部溫度較低。定子繞組的溫度分布為端部溫度較高，在軸向上從入風側到出風側溫度逐漸升高。轉子鐵心、轉子鼠籠上溫度分布規律分別類似于定子鐵心和定子繞組，只是其溫度差異沒有定子上的明顯。

這種溫度分布規律是由于電機內部發熱與散熱條件所決定的。定子繞組作為主要熱源之一，在定子槽內緊密嵌放，其熱量要經過槽內絕緣傳遞到定子鐵心，定子鐵心與機殼相接，這部分熱量最終從機殼上散發。風扇側空氣流速快，能夠帶走大部分熱量，但通過電機定子外殼的散熱風道到達另一端部時，風速減小，散熱能力下降，導致了電機溫度分布呈現軸向上的差異。

4.2 不同溫度下電磁場計算結果比較

利用以上溫度分布結果，本文進一步考察了電機在不同溫度下的性能變化。

以常溫（25℃）時的電機工作性能作為對照，比較最高溫度時電機性能變化。這里的最高溫度是指常溫環境下電機工作在額定負載時由溫度場計算得到最高溫度值。

圖6顯示的是電機負載時不同溫度下轉速曲線。圖中b曲線為常溫時轉速曲線，電機帶額定負載時轉速能達到1418 rpm，a曲線為最高溫度時轉速曲線，此時轉速僅能達到1409 rpm。溫度升高時，電機轉速略微下降，而且轉速的上升時間變長。

圖7顯示的是電機負載時不同溫度下氣隙磁密波形。a曲線為常溫時波形，b曲線為最高溫度時氣隙磁密波形。溫度升高使氣隙磁密波形產生畸變，最大氣隙磁密幅值略有降低。

以上計算均在電機溫升限度以內進行，因此，雖然電機性能隨溫度升高略有下降，但總體上還不至于使其無法正常工作。

5 結論

本文通過電磁場-熱場順序耦合的方式計算了五相鼠籠異步電機的三維溫度場分布，以該溫度分布為依據進行了不同溫度條件下電機的性能比較，結論如下：

1）不考慮附加的散熱條件下，電機溫度分布具有一定的對稱性，軸向剖面上的溫度場為中心對稱。另外，繞組及其端部發熱較嚴重，應著重改善其散熱條件；

2）通過有限元計算得到的電機溫度場分布能作為分析電機溫升限度的依據；

3）不同溫度條件下的電磁場計算結果驗證了溫度升高對電機性能的影響；

4）通過對電機溫度場的計算，為電機電磁和散熱設計打下基礎。

[1] Luigi Alberti, Nicola Bianchi, Peter Baldassari, Ren Wang. Thermal assisted finite element analysis of Eelectrical machines[C]//Proceedings of the 2008 International Conference on Electrical Machines. 2008: 1965-1969.

[2] Yang Mingfa, Zhang Peiming. Research on simplified 3D thermal model for the whole stator of asynchronous motor[J]. Proceedings of CSEE, 2010, 30: 203-208(in Chinese).

[3] Cao Junci, Li Weili, Cheng Shukang, Zhang Xiaochen. Temperature field calculation and associated factor analysis of induction motor with compound cage rotor[J]. Proceedings of the CSEE, 2008, 28(30): 96-103(in Chinese).

[4] Liu Huikai, Yang Li, Sun Fengrui. Study of surface temperature rise of induction motor with stator winding inter-turn short circuit fault in slot[J]. Transactions of China Electrotechnical Society, 2007, 22(3): 49-54(in Chinese).

[5] Wang Yanwu, Yang Li, Chen Xuan, Sun Fengrui. Study on 3D thermal field and thermal stress field of the induction motor rotor[J]. Electric machines and control, 2010, 14(6): 27-32.

[6] Wang Yanwu, Yang Li, Sun Fengrui. Simulation and analysis of 3D temperature field for stator winding short-circuit in asynchronous motor[J]. Proceedings of the CSEE, 2009, 29(24): 84-90(in Chinese).

[7] G.J.Li, J.Ojeda, E.Hoang, M.Gabsi. Thermal-electromagnetic analysis of a fault- tolerant dual -star flux-switching permanent magnet motor for critical applications[J]. IET Electric Power Applications, 2011, 5(6): 503-513.

[8] Aldo Boglietti, Andrea Cavagnino, David Staton. Determination of critical parameters in electrical machine thermal models[J]. IEEE Transactions on industry applications, 2008, 44(4): 1150-1159.

[9] Fabrizio Marignrtti, Vincenzo Delli Colli, Yuri Coia. Design of axial flux PM synchronous machines through 3-D coupled electromagnetic thermal and fluid-Dynamical finite-element analysis. IEEE Transactions on industrial electronics, 2008, 50(10): 3591-3601.

[10] Huang Yunkai, Hu Qiansheng, Zhu Jianguo. Magneto-thermal analysis of a high-speed claw pole motor considering rotational core loss[J]. Transactions of China Electrotechnical Society, 2010, 25(5): 54-60(in Chinese).

[11] Gu Chenglin, Chen Qiaofu, Xiong Yongqian. Electric Machines[M]. Wuhan: Huazhong university of science and technology press, 2005(in Chinese).

Modeling and Simulation Calculating of an Asynchronous Motor in 3D Thermal Field

Wang Zhijun1, Gao Zhongfeng2, Zhou Qian2

(1.Naval Aviation Academy，Jiyuan 454650, Henan, China; 2. No.91446 Unit of PLA, Zhuozhou 072750, Hebei, China)

TM343

A

1003-4862（2014）07-0030-05

2013-11-12

王治軍（1985-），男，助理工程師。研究方向：電機與電器。