微電機關鍵零部件尺寸偏差與性能偏差關系建模
潘躍林,張俊
?
微電機關鍵零部件尺寸偏差與性能偏差關系建模
潘躍林,張俊
(湘電集團股份有限公司特電事業部, 湖南湘潭 411101)
本文研究了微電機關鍵零部件尺寸偏差與性能偏差顯性關系建模的方法,微電機關鍵零部件尺寸偏差與性能偏差之間關系模型很難用常規的方法建模,因此本文先采用泰勒展開方法建立微電機關鍵零部件尺寸偏差與性能偏差關系的顯性數學模型,再運用Eviews進行回歸分析,并對回歸分析的結果進行分析研究,最終得到泰勒展開式的偏導系數,確定微電機關鍵零部件尺寸偏差與性能偏差關系的數學表達式。
微電機 尺寸偏差 性能偏差 泰勒展開 Eviews回歸分析
0 引言
企業要想提高市場競爭力就必須提高產品關鍵零部件質量,而提高產品關鍵零部件的質量需根據其性能要求對關鍵零部件的關鍵尺寸公差合理控制[1],為此研究產品零部件尺寸偏差與性能偏差的關系十分重要。有些產品關鍵零部尺寸偏差與性能偏差之間關系較為復雜,很難直接用常規的方法來求解,且產品關鍵零部件較多,要實現高維擬合難度較大,即使擬合出來精度也不會很高。本文采用泰勒展開式與回歸分析方法建立產品關鍵零部件尺寸偏差與性能誤差之間的關系模型,并以微電機為列驗證了該方法的可行性。
1 關鍵零部件尺寸偏差與性能偏差關系的分析
微電機質量輸出即空載電流1、空載轉速2、負載電流3、負載電速4與其關鍵零部件的尺寸即鐵芯高度1、軸的直徑2、機殼內徑3、后蓋同軸度4、機殼同軸度5、換向器直徑6有著一定的映射關系,但很難直接確定其顯性數學表達式,因此先假設微電機性能與微電機關鍵零部件的尺寸的關系如1式所示。




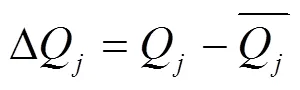


2 多元回歸分析
采用多元回歸分析的方法求解7式中的一階偏導數與二階偏導數,在Eviews軟件[3]中分別對微電機四個性能偏差與關鍵零部件尺寸偏差的樣本數據進行多次回歸分析,剔除回歸分析結果中的異常數據組,最后得到各性能偏差回歸分析的檢驗概率、決定系數、修正決定系數、德賓-沃森檢驗值如下。
2.1 空載電流偏差回歸模型
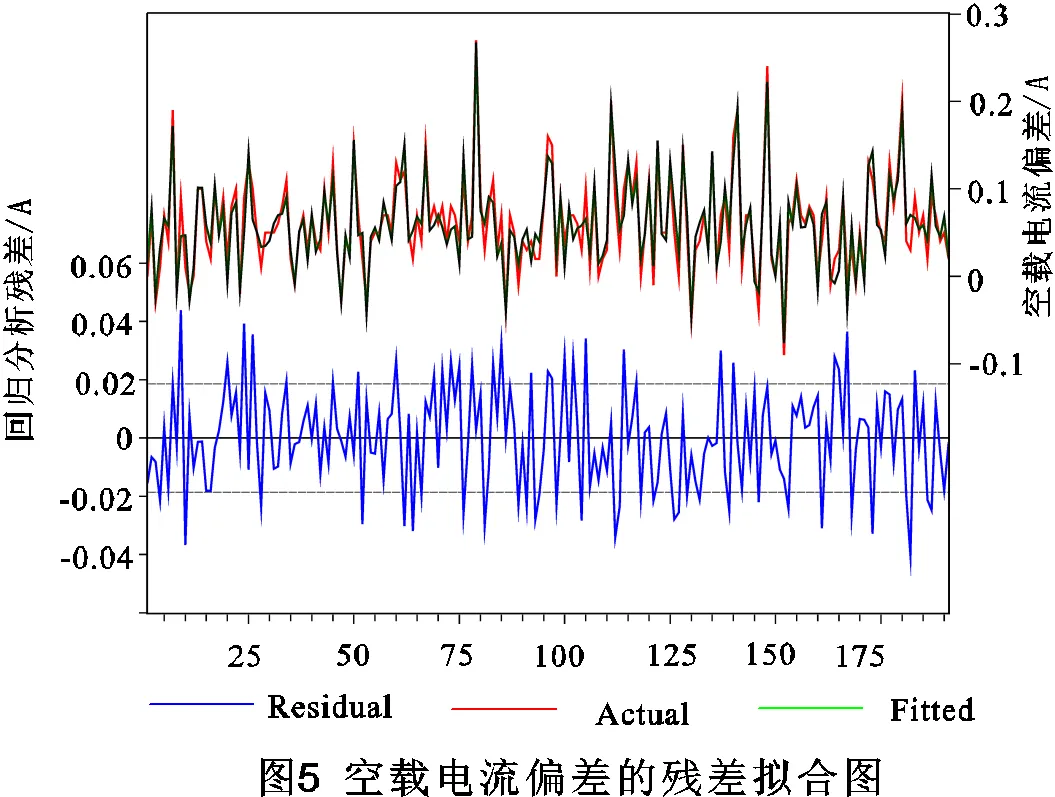
分析圖1、表1可看出空載電流偏差回歸模型的決定系數為0.852508,修正決定系數為0.825466說明自變量82.5466%的總離差平方和能被樣本回歸直線解釋,因此空載電流偏差的回歸直線對樣本擬合程度較高;德賓-沃森檢驗值為2.311002,接近2,因此回歸模型變量不存在序列自相關;27個待估計參數檢驗概率P中最大值0.0619比較小,且所有P接近0,因此均通過檢驗,說明空載電流回歸模型具有很強的顯著性,模型解釋能力強。圖5可看出空載電流偏差實際值與預測值的曲線基本吻合,且空載電流偏差的回歸模型其殘差值絕大部分在-0.02至0.02范圍內。
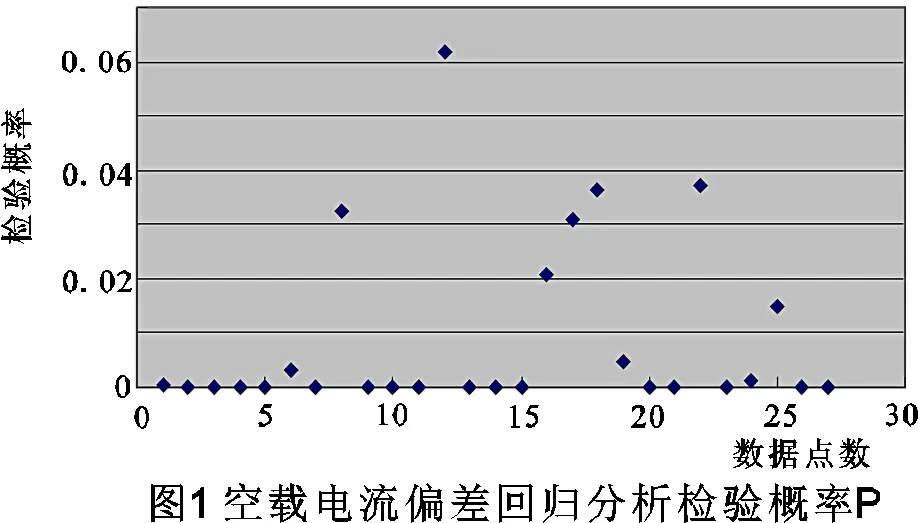

圖6可看出空載電流偏差回歸模型的殘差基本符合正態分布,殘差最大值為0.043879,最小值為-0.040196。圖7可看出空載電流偏差與回歸模型殘差平方沒有固定規律,因此有空載電流偏差的回歸模型不存在異方差性問題。
上述分析可知空載電流偏差回歸模型較為理想,由回歸分析可得微電機空載電流偏差與關鍵零件部尺寸偏差之間的數學表達式如8式所示。
2.2 空載轉速偏差回歸模型分析
圖2、表1可知空載轉速偏差回歸模型的決定系數為0.891029,修正決定系數為0.886436,說明自變量88.6436%的總離差平方和能被樣本回歸直線解釋,因此空載轉速偏差的回歸直線對樣本擬合程度相當理想;德賓-沃森檢驗值為1.865217,接近2,因此回歸模型變量不存在序列自相關;27個待估計參數的檢驗概率中最大值0.0692較小,且所有P值接近0,因此均通過檢驗,說明空載轉速回歸模型具有很強的顯著性, 模型解釋能力強。
圖8可看出空載轉速偏差實際值與預測值的曲線基本吻合,且空載轉速偏差的回歸模型其的殘差值大部分在-30至30范圍內。

圖9為空載轉速偏差殘差的直方圖,由圖可知空載轉速偏差回歸模型的殘差基本符合正態分布,殘差最大值為50.83692,最小值為-54.58296。
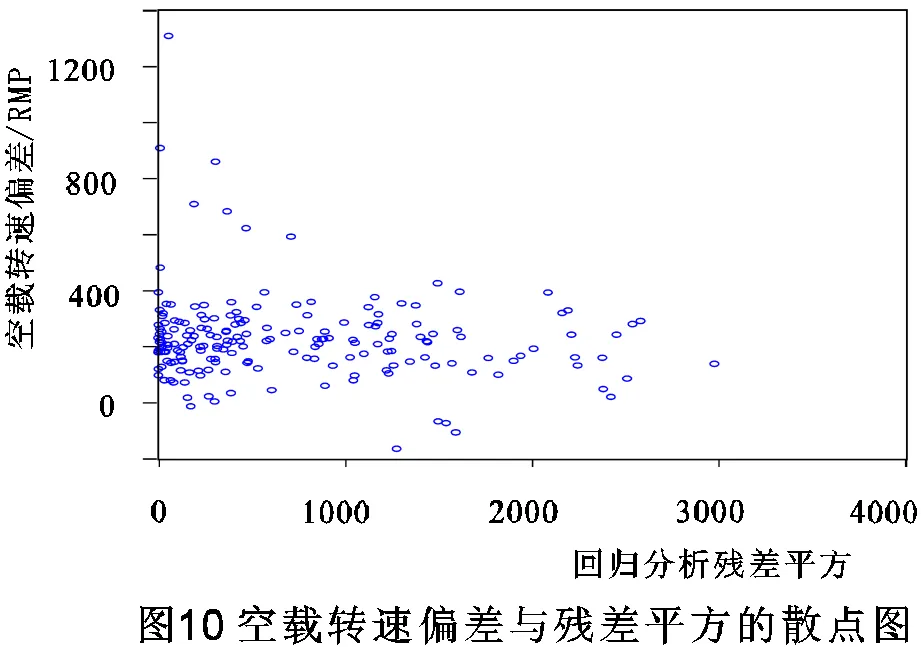
圖10可看出空載轉速偏差與回歸模型殘差平方沒有固定規律,因此有空載轉速偏差回歸模型不存在異方差性問題。
上述分析可知空載轉速偏差回歸模型較為理想,由回歸分析可得微電機空載轉速偏差與關鍵零件部尺寸偏差之間的數學表達式如9式所示。
2.3 負載電流偏差回歸模型分析
圖3、表1可知負載轉速偏差回歸模型的決定系數為0.863352,修正決定系數為0.841688,說明自變量84.1688%的總離差平方和能被樣本回歸直線解釋,因此負載電流偏差的回歸直線對樣本擬合程度比較理想。德賓-沃森檢驗值為2.094273,接近2,因此回歸模型變量不存在序列自相關;27個待估計參數的檢驗概率P中最大值0.0563較小,且所有P值接近0,因此均通過檢驗,說明負載轉速偏差回歸模型具有很強的顯著性, 模型的解釋能力強。
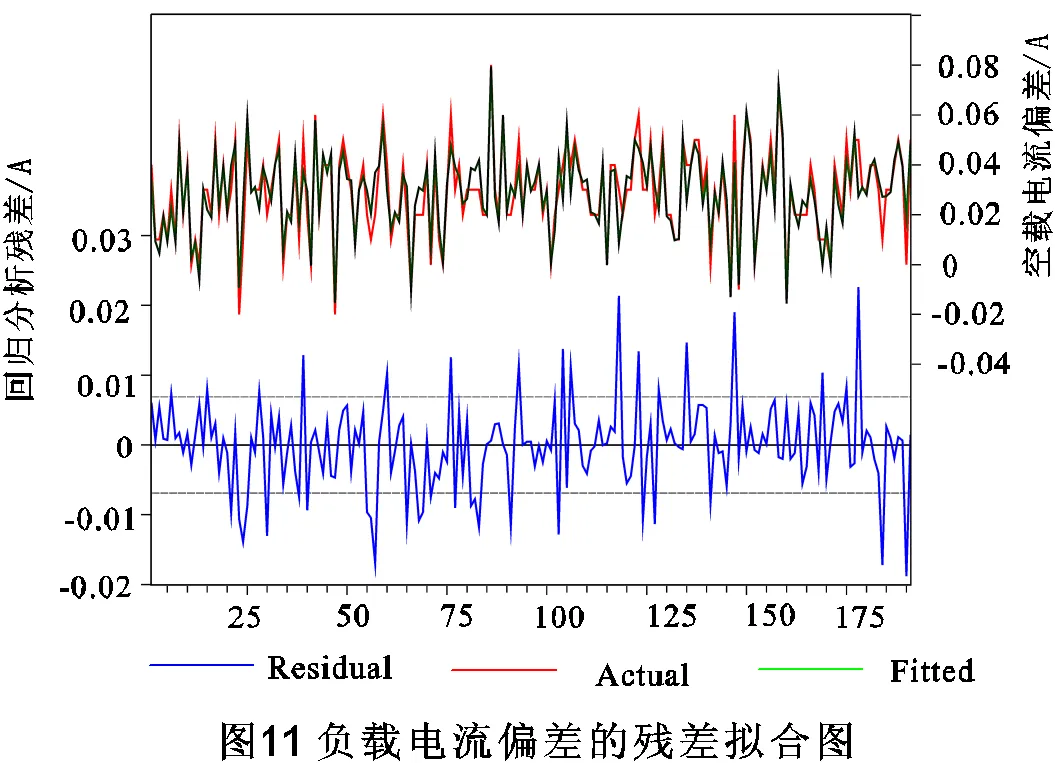
圖11可看出負載電流偏差實際值與預測值的曲線基本吻合,且負載電流偏差回歸模型的殘差值大部分在-0.007至0.007范圍內。
圖12可看出負載電流偏差回歸模型殘差基本符合正態分布,殘差最大值為0.02258,最小值為-0.018798。
圖13可看出負載電流偏差與回歸模型殘差平方沒有固定規律,因此有負載電流偏差回歸模型不存在異方差性問題。上述分析可知負載電流偏差回歸模型較為理想,由回歸分析可得微電機負載電流偏差與其關鍵零件部尺寸偏差直接的數學表達式如10式所示。
2.4 負載轉速偏差回歸模型分析
由圖4、表1可知負載轉速偏差回歸模型決定系數為0.898423,修正決定系數為0.883417,說明自變量88.3417%的總離差平方和能被樣本回歸直線解釋,因此負載轉速偏差的回歸直線對樣本的擬合程度較理想;德賓-沃森檢驗值為2.066249,接近2,因此回歸模型變量不存在序列自相關;27個待估計參數的檢驗概率P中最大值0.0591較小,且所有P值接近0,因此均通過檢驗,說明負載轉速偏差回歸模型具有很強的顯著性,模型的解釋能力強。
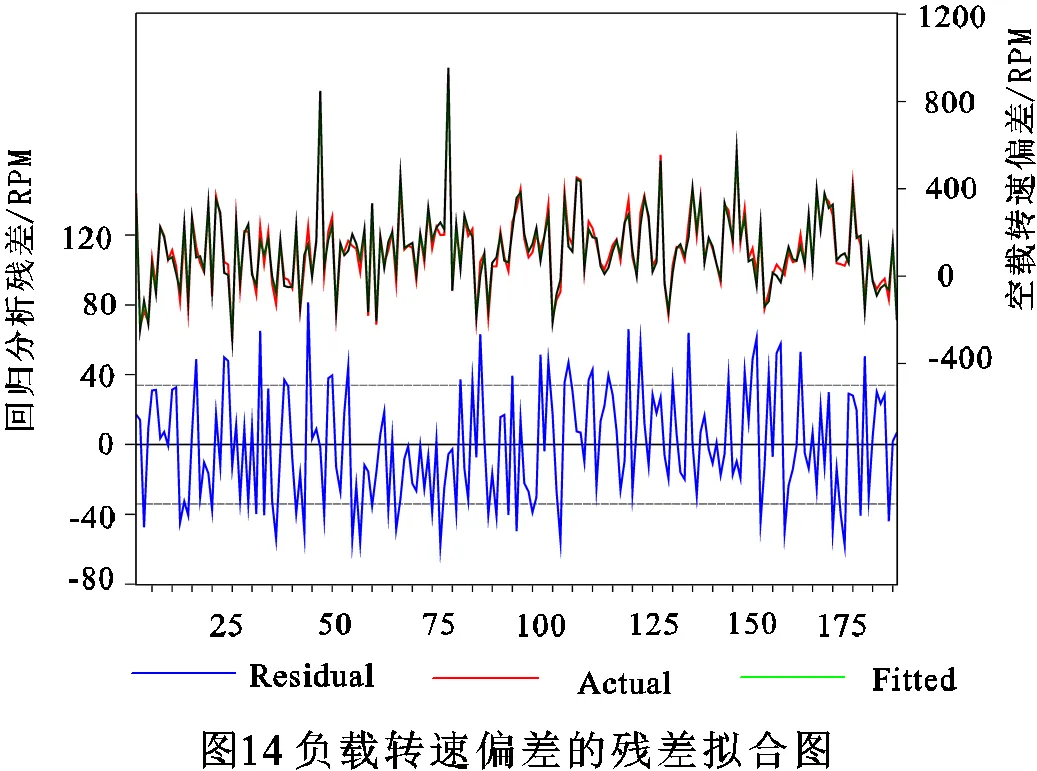
圖14可看出負載轉速偏差實際值與預測值的曲線基本吻合,且負載轉速偏差的回歸模型的殘差值大部分在-35至35范圍內。
圖15可看出負載轉速偏差與回歸模型殘差平方沒有固定規律,因此負載轉速偏差回歸模型不存在異方差性問題。
上述分析可知負載轉速偏差回歸模型較為理想,由回歸分析可得微電機負載轉速偏差與其關鍵零件部尺寸偏差之間的數學表達式如11式所示。
3 結論
本文研究了微電機關鍵零部件尺寸偏差與性能偏差關系建模的方法,微電機關鍵零部件尺寸偏差與性能偏差之間關系非常復雜,因此采用泰勒展開方法建立微電機關鍵零部件尺寸偏差與性能偏差關系的數學模型,運用回歸分析方法計算出泰勒展開式的偏導數,并對回歸模型擬合情況分析,最后確定微電機關鍵零部件尺寸偏差與性能偏差關系的數學表達式。
[1] 吳昭同,余忠華,陳文華.保質設計[M].北京:機械工業出版社,2004.
[2] BEYER H G, SENDHOFF B. Robust optimization a comprehensive survey [J].Computer Methods in Applied Mechanics and Engineering, 2007, 196(33):3190-3218.
[3] 攸頻,張曉峒. Eviews 6實用教程[M]. 北京:中國財經出版社, 2008.
Modeling of Key Parts Dimension Deviation and Performance Deviation for Micro-motor
Pan Yuelin, Zhang Jun
(Xiangtan Electric Group Co. Ltd, Xiangtan 411101, Hunan,China)
TM382
A
1003-4862(2014)07-0075-06
2014-05-17
潘躍林(1977-),男,工程師。研究方向:電機。

