波浪相位對航行體出水過程水動力特性的影響

朱坤，陳煥龍，劉樂華，楊曉光，張紀華

(1.北京機電工程研究所，北京100074;2.哈爾濱工業大學 能源科學與工程學院，黑龍江 哈爾濱150001)

0 引言

現代高技術戰爭日趨重視對敵的精確縱深打擊與對己的隱身保護，而潛射導彈在這兩方面均具有非常明顯的優勢。它兼有潛艇的隱蔽性好、機動范圍大、生存能力強的特點和導彈的射程遠、打擊精度高、破壞性強的優點。自導彈誕生初期，潛射導彈的發展就備受關注，并逐漸成為當前核威懾和實施二次核打擊的中堅力量［1］。因此，世界各軍事強國均對潛射導彈的研制投入了大量的人力和物力。潛射導彈發射過程主要包括水下運動過程、出水過程以及空中飛行過程，其中以出水過程的力學環境最為復雜，它涉及到出水過程介質突變及其伴隨的空泡幾何特性變化與潰滅問題。其中在復雜海情條件下的因空泡變形、潰滅而對彈體產生的沖擊與結構破壞問題一直倍受廣大學者與相關科研人員的關注。

關于航行體出水問題Von Kármáan 早在1929年做了開創性的理論模型研究工作［2］，這一研究工作對于現代導彈和魚雷水下發射技術的發展具有重要的理論意義［3］。航行體高速出水過程的局部空化問題是影響其飛行姿態與精確打擊目標的重要因素之一?？栈鲌鼋Y構對于水下航行體的水動力特性、水載荷以及穩定性控制等都具有重要的影響，空泡流動特性及其機理研究始終是水動力學研究的前沿課題之一。文獻［4］采用自行開發的程序對水翼空化流場的研究表明，在大攻角條件下，空泡閉合區后的逆壓梯度導致渦的形成及回射流的發展，沿壁面逆向流動的混合介質射流是引起空泡斷裂的原因，回射流發展、渦結構變化與空泡非穩態演化過程存在密切聯系，并探討了翼型空泡周期性脫落的一些機理問題。文獻［5］從理論和試驗研究角度出發，分析了導彈出水過程中頭部空泡產生的物理機制、導彈出水過程中空泡潰滅對彈體動力學特性的影響以及出水后導彈的氣動特性等氣/水動力學問題。此外，諸多學者通過對空化物理本質的深入研究，試圖建立和發展空化模型，并將其耦合于大型計算流體力學(CFD)程序或商業軟件中，以期解決更多的工程實際問題［6-8］。影響導彈出水姿態與打擊目標精度的又一重要因素是海情條件，而海情條件中的一個重要因素就是波浪或海浪。關于波浪中航行體的水動力與水載荷計算方法，可以追溯至1955年Korvin-Kroukovsky［9］切片概念的提出。到了20世紀70年代，這方面的研究常常采用多極展開法［10-11］與源分布密切擬合法［12］。近年來，隨著計算技術的發展，更多的是采用求解常微分方程與N-S 方程耦合的全三維方法［13-15］。文獻［16］則將波浪載荷對運載器出水姿態的影響視為潛射導彈運載器水下發射的一項關鍵性技術。

綜上所述，航行體出水過程的流體動力學應用基礎研究對于水下發射關鍵技術的突破具有重要意義。但是，由于物理問題的復雜性，考慮波浪并耦合空泡流動非定常、非線性影響的航行體水下發射研究工作開展相對較少。因此，研究近水面波浪與空化耦合流動機制對航行體水下發射技術研發具有非常重要的學術意義與實際工程應用價值。

1 數值方法及其驗證

1.1 Mixture 模型方程

Mixture 模型的連續性方程形式為

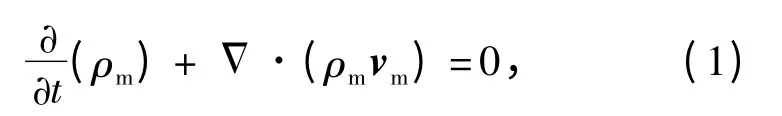
式中:vm為平均速度矢量;ρm為混合物的密度。

Mixture 模型的動量方程是通過累積求和各相獨自的動量方程而來的，其表達式如(2)式所示。

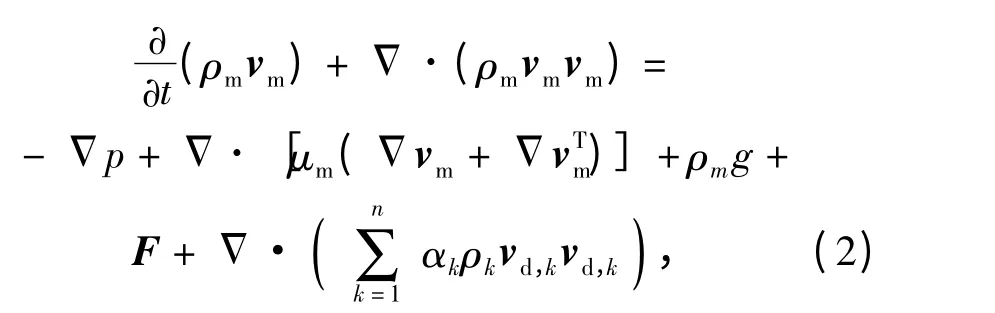
式中:n 為相數;F 為體積力矢量;μm為混合物動力粘性系數;vd，k為次相k 的滑移速度矢量;g 為重力加速度矢量;αk為第k 相的體積分數。

1.2 空化模型

空化過程在多相流動中表現出強烈的非線性特征，通常所遇到的空化現象都發生在兩相流體之間，可通過氣相輸運方程求得發生空化現象的兩相流體之間的關系，其表達式為

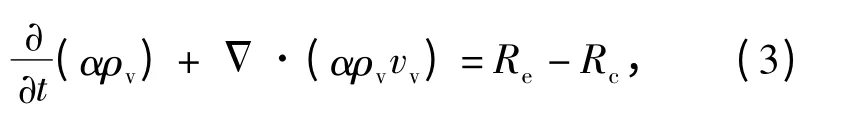
式中:α 為氣相體積分數;ρv為氣相密度;vv為氣相速度矢量;Re為空泡產生源項;Rc為潰滅源項。

為描述空泡的變化規律，文中采用Zwart 等［17］修正的空化模型對Re和Rc進行?；?，具體表達式為

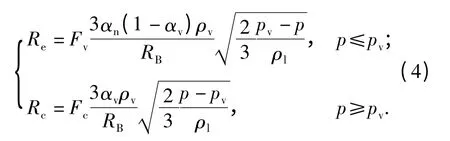
式中:p、pv分別為當地壓力和氣泡表面壓力;RB為空泡發展過程中的微小氣泡半徑;ρl為液體密度;αn為氣核體積分數;Fv為蒸發系數;Fc為凝結系數。文中取RB=10-6m，αn=5×10-4，Fv=50，Fc=0.001.

1.3 數值方法驗證

為了驗證文中所采用的計算方法與計算模型的可靠性和求解精度，通過采用多相流模型與計算方法對文獻［18］的實驗模型進行數值模擬研究，并獲取其表面壓力系數Cp分布與相應的實驗數據進行對比分析，如圖1所示(橫坐標L 為模型長度，x 為位置坐標)。研究結果表明，本文所采用的計算方法與數學模型，不僅能夠比較準確預測空泡的大小，而且對于空泡末端回射壓力峰值的計算也可以取得令人滿意的效果。因此，該數值方法與數學模型可以滿足文中的研究需求。

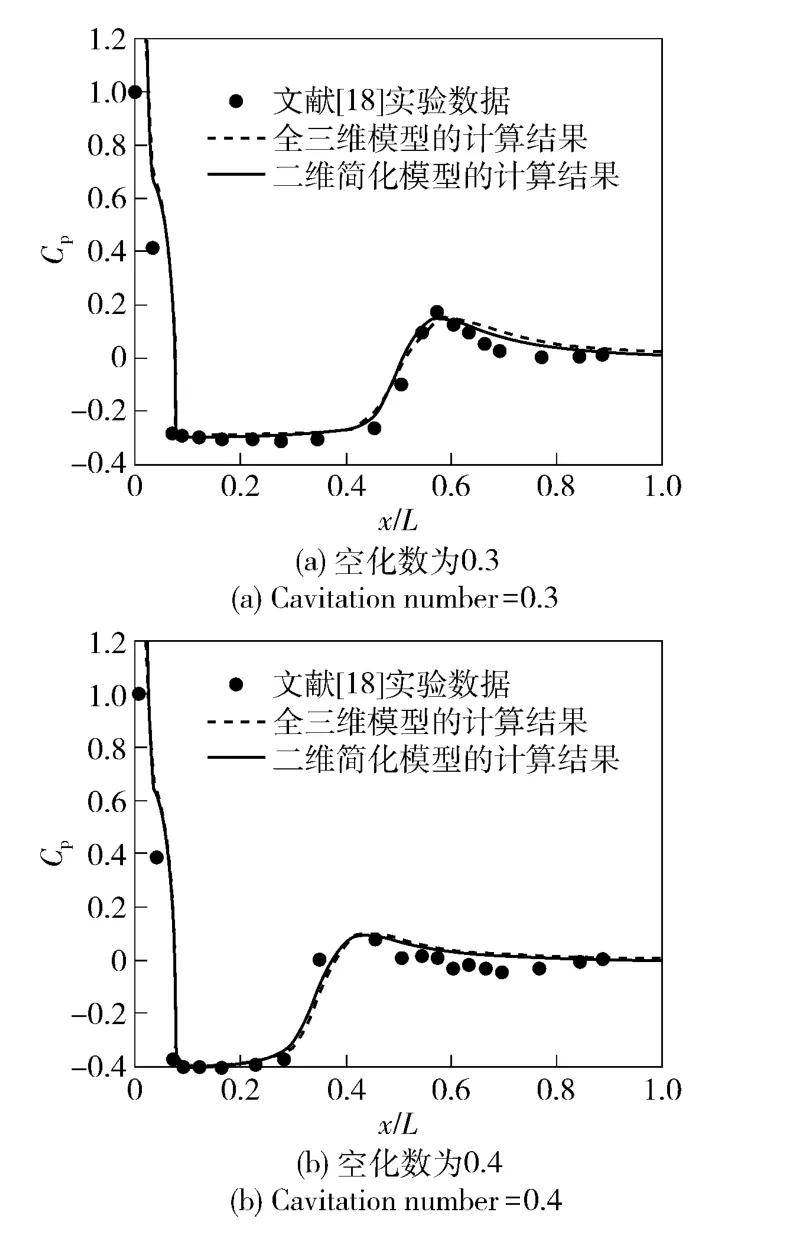
圖1 某航行體表面壓力系數分布Cp 對比分析(來流攻角為0°)Fig.1 Comparqtive analysis of surface pressure coefficient Cp(angle of attack:0°)

2 研究結果分析與討論

根據初期的研究思路，擬定了表1的4 個不同波浪相位的研究方案。波浪的傳播規律采用5 級浪的二階Stokes 非線性波，其主要波浪參數見表1，波浪相位的定義如圖2所示。

圖1中，相位角θ =0°表示航行體頭部接觸波面時位于波谷位置，相位角θ =180 °表示航行體頭部接觸波面時位于波峰位置，相位角θ 等于90°與270°表示航行體頭部接觸波面時位于波峰與波谷之間位置。圖3給出了本文數值計算時采用的計算域，其尺寸為90 m×30 m×80 m，其選取原則:首先要保證航行體頭部距離靜水面為30 m，同時水面上需要留出足夠的空間以保證航行體能夠完全出水;其次要保證在波浪傳播方向上至少具有2 倍波長的距離，否則對于波浪的模擬將會存在較大的誤差。圖4給出了后續數據分析所需的航行體分段示意圖。

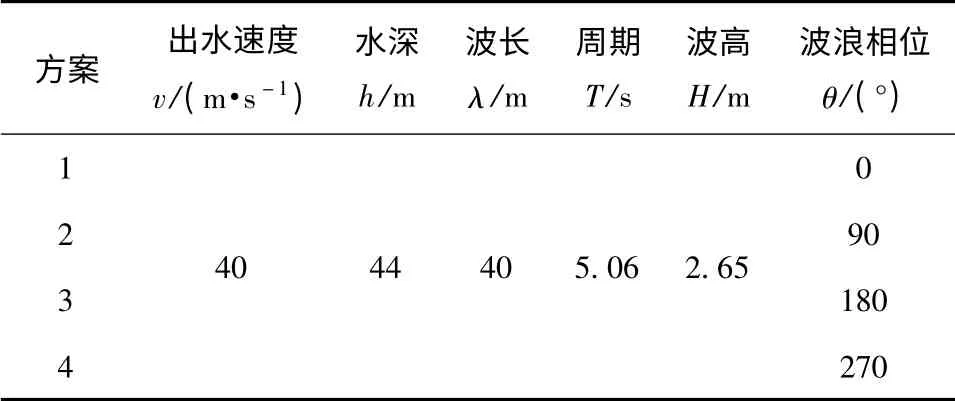
表1 研究方案Tab.1 Research schemes

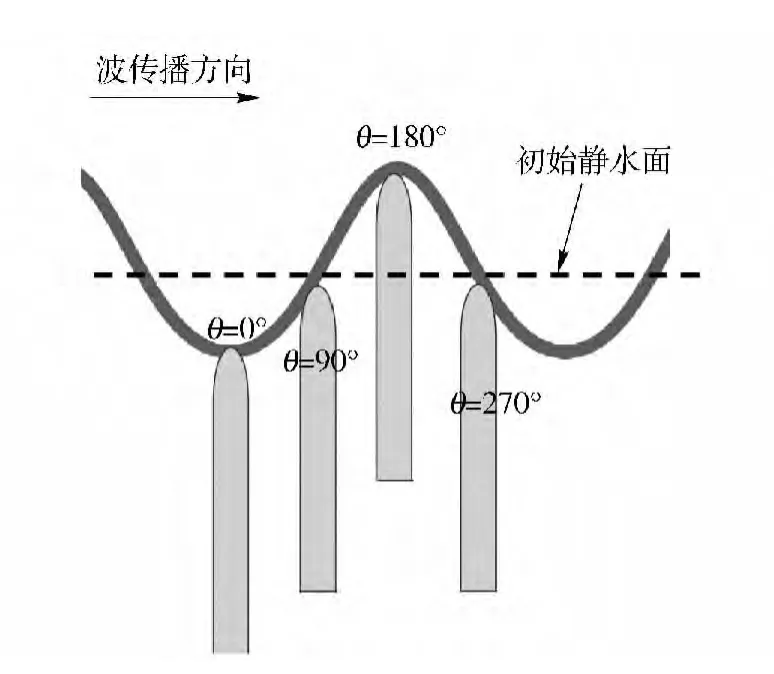
圖2 波浪相位定義Fig.2 The definition of wave phase

結合本文研究對象的幾何與運動特征，采用結構化與非結構化相結合的混合網格方式，并使用層變方式的動網格更新技術。在航行體壁面附近進行了局部網格加密處理，保證了y+值滿足湍流模型的要求，并在研究過程中進行了網格無關性的驗證。同時為了提高航行體周圍的網格質量，在航行體外圍設計了合適的網格包裹區域。

圖5給出了航行體頭部附近1 ～6(具體位置見圖4)位置的表面壓力積分時變特性。研究結果表明，在航行體出水過程中，對于產生空化流動的區域其壓力呈現先降低后增加的變化規律，空泡內部航行體表面的壓力梯度基本為0.隨著肩空泡的尺寸的減小，泡內壓力在較短時間內從臨界壓力迅速增加至大氣壓，且出水過程中同一時刻波峰位置相位下的壓力最低，而波谷位置相位下的壓力最高，如2 ～6部分，這與波峰相位下空泡的作用時間較長有關;對于非空化區域，隨著航行體頭部與水面距離的減小，其表面靜壓隨時間的增加而降低，且出水過程中同一時刻波峰位置相位下的壓力最高，而波谷位置相位下的壓力最低。航行體頭部滯止區域在出水過程壓力梯度較大，當航行體位于波峰位置出水時，由于頭部接觸水面較晚，所以壓力較高，如1 部分。3 ～6 部分，由于在運動過程中部分區域處于肩部空泡區域，所以它們在某一時段其表面壓力積分值基本不隨時間變化，這一時段的大小反應了肩部空泡在該位置的作用時間長短，尤其是4 與5 區域，基本處于肩部空泡內部，因此其壓力保持不變的時段最長，而3 與6 位置則只有部分區域處于肩空泡的前端與末端。

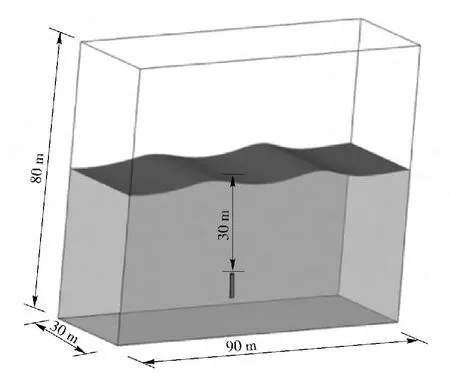
圖3 計算域的選取Fig.3 The selection of computational domain

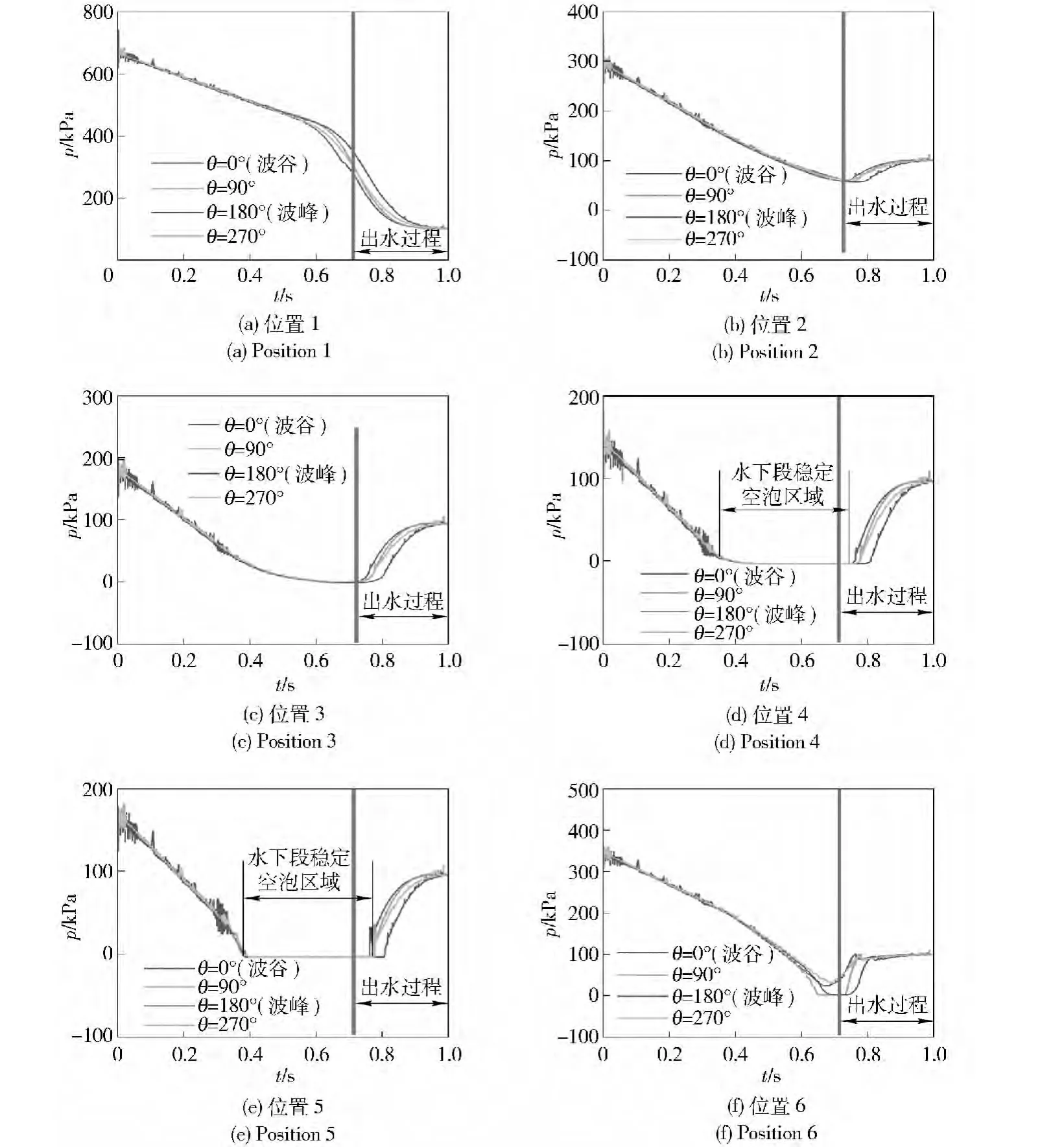
圖5 局部壓力分布時變特性Fig.5 The time-dependent local pressure distribution characteristics

表2給出了航行體不同出水相位條件下出水過程近水面肩空泡幾何特性與壓力場分布規律。研究結果表明，在近水面由于航行體受到波浪表面性與相位的影響，航行體在波谷(θ =0°)與波峰(θ =180°)相位出水時，肩部空泡形態在周向表現為不對稱的幾何特征，相應的壓力載荷也表現為不對稱的分布規律—肩空泡在航行體軸向覆蓋的距離越大則航行體肩部低壓區的尺度亦越大?？梢酝茰y在實際的發射環境中，出水過程航行體肩空泡的潰滅方式為非對稱潰滅，其潰滅瞬間產生的潰滅壓力對航行體造成巨大沖擊力與俯仰力矩，這直接影響航行體出水姿態與打擊空中目標的效果。航行體在其他兩個中間相位出水時，其空泡幾何形態的空間對稱性相對較好，因此，其肩部壓力載荷的分布也較為理想，這對于實際航行體出水姿態的影響較小。尤其是當航行體在θ =270°相位下出水時，不僅航行體肩部空泡的對稱性最好，迎背水側的肩空泡長度差最小，而且空泡的軸向尺寸最小，肩空泡存在的時間最短，相應的壓力場分布也表現為類似的特征。因此，在當前的研究條件下，θ=270°為最優出水波浪相位。

表2 不同相位近水面空泡幾何特性與壓力分布Tab.2 The pressure distribution and cavity geometry characteristics near the free surface about different wave phases

此外，通過對比分析，研究結果進一步表明，除了航行體在波谷(θ =0°)相位下出水的情況外，其它波浪相位下出水時，航行體肩空泡的軸向幾何尺寸均表現為背水面軸向尺寸大于迎水面軸向尺寸。航行體波峰位置(θ =180°)出水時，肩空泡的對稱性最差，迎背水側的肩空泡長度差最大，肩空泡存在的時間最長(由于水下運動的時間最長)，空泡體積最大，航行體肩部的水動力環境最為惡劣，出水過程中將嚴重影響航行體的出水姿態。這種由于波浪作用而產生的航行體肩部空泡幾何嚴重不對稱，將引起航行體力學載荷的波動與對航行體造成的沖擊更加劇烈。因此，在實際水彈道、水動力設計以及發射海情環境的選擇中應該盡量避免航行體波峰位置出水的情況。而出水相位為θ =270°時，肩空泡的對稱性最好，空泡體積最小，該方案為水彈道設計的首選出水相位方案。

前面的分析表明，航行體處于不同波浪相位出水時，其肩部附近的流場結構、水動力與水載荷參數存在明顯的差異，產生這種差異的物理機制與波浪導致近水面流體質點的動力學特性在波谷與波峰的巨大差異有關。

根據物理學中波的傳播理論，任意一個波峰或波谷位置的兩側對應空間位置，流體質點的運動方向相反。因此，流體質點的運動方向隨波長方向呈現周期性變化規律。在每一個波長范圍內，流體質點的速度矢量方向呈正負交替變化。對于本文的研究對象而言，波峰相位區域流體質點速度矢量方向逆時針旋轉，而在波谷相位區域流體質點速度矢量方向順時針旋轉。而且，波峰與波谷區域均處于流體質點剪切流動的旋渦中心，具有最大的渦量分布，壓力較低，為航行體肩空泡的產生與發展提供了得天獨厚的條件，尤其是波峰區域效果更為明顯。由于流體質點剪切流動的不均勻性，導致了肩空泡三維空間的不對稱性。0°和270°相位處為波峰、谷速度矢量場方向的交界位置，流體質點速度方向沿X 軸發生正負轉變，為峰、谷影響區交替點，流體的剪切運動相對較弱，因此航行體肩空泡的三維空間對稱性較好，如圖6所示。

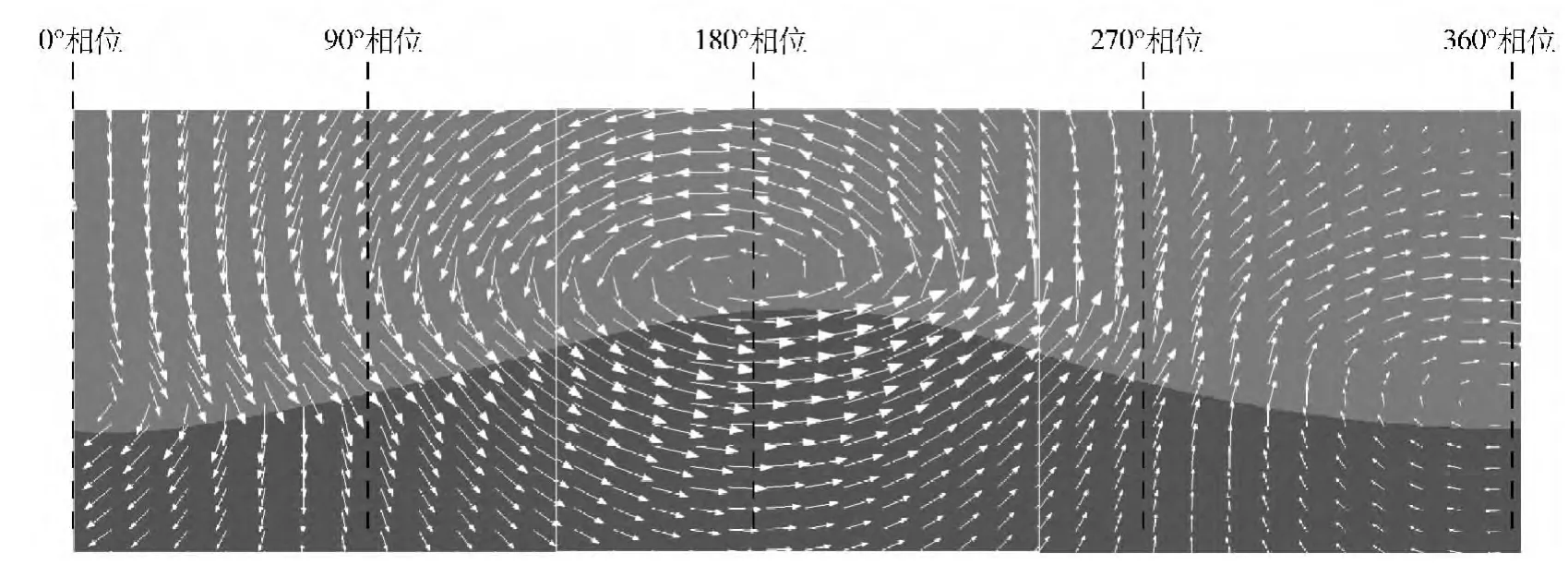
圖6 波面附近流體質點的運動規律Fig.6 The motion rules of fluid particles near the wave surface

3 結論

在不同波浪相位條件下，對某潛射航行體出水過程水動力學特性與近水面空泡流場結構進行了數值研究，獲得了相關的水動力學與空泡流動參數，探討了波浪相位對航行體近水面肩空泡流場結構影響的物理機制，得到如下結論:

1)在航行體出水過程中，空泡作用的航行體位置表面壓力分布特征為先減小后增加，且波峰位置(θ=180°)出水時航行體肩空泡作用時間最長，航行體出水過程表面壓力梯度最大，而波谷位置出水時情況恰好相反。

2)波浪相位的差異導致航行體肩部空泡空間幾何的不對稱，進而引起航行體表面水動力分布的不對稱性。其中，出水相位角θ =0°時，近水面區域航行體肩空泡的軸向尺寸表現為迎水面大于背水面，而其他出水相位角的情況恰好相反。

3)近水面流體質點剪切運動的強弱與方向是導致航行體肩空泡空間不對稱結構的一個重要因素。航行體處于θ =270°中間相位出水時，水動力參數在周向具有較好的對稱性，屬于本次研究的航行體最優出水相位。

References)

［1］ 鄭幫濤.潛射導彈出水過程水彈道及流體動力研究進展［J］.導彈與航天運載技術，2010，5:8 -11.ZHENG Bang-tao.Overview on hydroballistics and fluid dynamics of submarine-based Missiles［J］.Missiles and Space Vehicles，2010，5:8 -11.(in Chinese)

［2］ Von Kármán T.The impact on seaplane floats during landing［R］.US:National Advisory Committee for Aeronautics，1929.

［3］ 魯傳敬.軸對稱細長體的垂直出入水［J］.水動力學研究與進展:A 輯，1990，5(4):35 -41.LU Chuan-jing.The vertical water exit and entry of a slender axisymmetric body［J］.Journal of Hydrodynamics:Ser A，1990，5(4):35 -41.(in Chinese)

［4］ 陳瑛，魯傳敬，郭建紅.翼型空泡周期性流動的數值模擬及機理分析［J］.應用力學學報，2011，28(1):1 -6.CHEN Ying，LU Chuan-jing，GUO Jian-hong.Numerical simulation and mechanism analysis on the periodic cavitating flow around hydrofoil［J］.Chinese Journal of Applied Mechanics，2011，28(1):1 -6.(in Chinese)

［5］ 羅金玲，毛鴻羽.導彈出水過程中氣/水動力學的研究［J］.戰術導彈技術，2004(4):23 -25.LUO Jing-ling，MAO Hong-yu.Research on aerodynamics and hydrodynamics in exiting water process of missile［J］.Tactical Missile Technology，2004(4):23 -25.(in Chinese)

［6］ Singhal A K，Athavale M M，Li H，et al.Mathematical basis and validation of the full cavitation model［J］.Journal of Fluids Engineering，2002，124(3):617 -624.

［7］ Kubota A，Kato H，Yamaguchi H.A new modeling of cavitating flows:a numerical study of unsteady cavitation on a hydrofoil section［J］.Journal of fluid Mechanics，1992，240(1):59 -96.

［8］ Kunz R F，Lindau J W，Billet M L，et al.Multiphase CFD modeling of developed and supercavitating flows，ADP012082［R］.Brussels，Belgium:Pennsylvania State Univ University Park Applied Research Lab，2001.

［9］ Korvin-Kroukovsky B V.Investigation of ship motions in regular waves［M］.Washington，DC:SNAME，1955.

［10］ Ursell F.On the heaving motion of a circular cylinder on the surface of a fluid［J］.The Quarterly Journal of Mechanics and Applied Mathematics，1949，2(2):218 -231.

［11］ Tasai F.Formula for calculating hydrodynamic force on a cylinder heaving in the free surface，N-parameter family［R］.Kyushu:Research Institute for Applied Mechanics，1960，31:71 -74.

［12］ Frank W.Oscillation of cylinders in or below the free surface of deep fluids，AD-668338［R］.Bethesda，MD:David W Taylor Naval Ship Research and Development Center Bethesda MD Dept of Hydromechanics，1966.

［13］ 匡曉峰，汪玉，繆泉明，等.水下航行體波浪力理論預報［J］.船舶力學，2006，10(1):28 -35.KUANG Xiao-feng，WANG Yu，MIAO Quan-ming，et al.Theory prediction of wave forces for a deep-submerged body［J］.Journal of Ship Mechanics，2006，10(1):28 -35.(in Chinese)

［14］ 劉曜.波浪對運載器出水姿態角的影響［J］.艦船科學技術，2005，27(3):32 -34.LIU Yao.Wave effect on a submerged missile capsule traveling near-surface［J］.Ship Science and Technology，2005，27(3):32 -34.(in Chinese)

［15］ 田兵，徐新琦，肖鵬飛.波浪對潛地彈道導彈出水運動的影響［J］.艦船科學技術，2009，31(4):81 -84.TIAN Bing，XU Xin-qi，XIAO Peng-fei.Wave effect on the exceeding water motion of submarine-to-ground ballistic missile［J］.Ship Science and Technology，2009，31(4):81 -84.(in Chinese)

［16］ 姚奕，聶永芳，馮林平.潛射導彈運載器水下發射關鍵技術研究［J］.飛航導彈，2010(2):56 -59.YAO Yi，NIE Yong-fang，FENG Lin-ping.The investigation of underwater launch key technology in submarine-launched missile［J］.Aerodynamic Missiles Journal，2010(2):56 - 59.(in Chinese)

［17］ Zwart P J，Gerber A G，Belamri T.A two-phase flow model for predicting cavitation dynamics［C］//Fifth International Conference on Multiphase Flow.Yokohama，Japan:The Japanese Society for Multiphase Flow，2004.

［18］ 權曉波，李巖，魏海鵬，等.大攻角下軸對稱航行體空化流動特性試驗研究［J］.水動力學研究與進展:A 輯，2008，23(6):662 -667.QUAN Xiao-bo，LI Yan，WEI Hai-peng，et al.An experiment study on cavitation of underwater vehicle’s surface at large angles of attack［J］.Journal of Hydrodynamics:Ser A，2008，23(6):662 -667.(in Chinese)