基于理想視線的彈道成型最優(yōu)導引律

李浩，佘浩平

(北京理工大學 宇航學院，北京100081)

0 引言

現(xiàn)代精確制導武器重要的發(fā)展方向是強抗干擾能力、遠射程和高精度制導。盡管近年來導引頭探測和跟蹤技術水平已大幅提高，但同時目標隱身技術也在同步發(fā)展，導引頭的探測距離遠不能滿足遠程攻擊射前截獲的要求，遠程攻擊的主要模式還是基于遠程數(shù)據(jù)鏈和尋的導引頭的復合制導體制。

目前，尋的導彈的中、末制導導引律一般均采用比例導引律，這是由于比例導引律形式簡單且需要的制導信息少的緣故。然而，當導彈在復雜背景下進行攻擊，例如攻擊低空下視目標時，比例導引所形成的彈道必然是俯沖攻擊，導引頭要在復雜的地物背景和地雜波的情況下完成對目標的截獲和跟蹤，目標信號可能淹沒在極強的雜波干擾中。為了克服或減小這種影響，對中制導彈道進行規(guī)劃是一個合理的思路。由于中制導數(shù)據(jù)鏈一般能夠提供包括目標的位置、速度等較為豐富的制導信息，利用這些信息可以對中制導彈道進行成型設計，使得中末制導交接和末制導時段內(nèi)彈目視線滿足抬頭攻擊的要求，這樣就能避免或減小導引頭接收到的雜波干擾。

近年來，國內(nèi)外學者對彈道成型導引律開展了較多的研究［1］，主要的研究內(nèi)容集中在基于最優(yōu)控制理論和基于比例導引理論進行彈道成型控制兩個方面。基于最優(yōu)控制理論的彈道成型導引律在文獻［2］中首次提出，該文研究側(cè)重于終端姿態(tài)角約束條件下線性制導系統(tǒng)的最優(yōu)控制。文獻［3］提出了彈道軌跡可預測條件下的機動目標攻擊使用的彈道角約束最優(yōu)導引律。文獻［4］利用最優(yōu)控制理論推導了存在動力學滯后時的末端彈道成型導引律，可以滿足期望的終端攻擊要求。文獻［5］在最優(yōu)控制理論和微分對策理論的基礎上，利用零效脫靶量概念推導了末端彈道成型導引律，在目標機動和較大前置角誤差的情況下仍具有良好的性能。文獻［6］在彈道成型導引律的基礎上加入對攻擊終端時間約束條件，利用最優(yōu)控制理論完成了同時帶有攻擊時間和末端彈道角度約束的導引律，可以實現(xiàn)對低機動目標的協(xié)同飽和攻擊。文獻［7］中實現(xiàn)了過載的幅值約束和末端彈道角約束，但導引律表達形式復雜，不適合工程應用。基于比例導引理論的彈道成型導引律主要有兩種類型:偏置比例導引(BPN)律和分段比例導引律。BPN 律首先在文獻［8］中被提出，在傳統(tǒng)比例導引律的基礎上，加入與剩余距離相關的偏置過載，可以完成對末端角度的約束。文獻［9 -10］從不同的角度對BPN 律進行了完善，解決了偏置過載需求過大，飛行初段無法得到目標視線信息等問題。文獻［11 -12］基于傳統(tǒng)比例導引理論，分別針對固定目標和勻速目標設計了分段比例導引律，攻擊的第一階段控制導彈爬升和平飛，并根據(jù)比例導引律的彈道特性實時計算視線角參數(shù)，當參數(shù)值滿足所需終端視線角要求時，切換比例導引系數(shù)進入比例導引的第二階段，完成對目標的俯沖攻擊。此外滑模變結構控制理論也在彈道成型導引律設計方面有著較多應用，文獻［13］在考慮了自動駕駛儀動力學特性的基礎上，利用滑模變結構控制理論完成了相應導引律的設計。

本文基于最優(yōu)控制理論，在考慮彈道過載合理分配的情況下，提出了一種終端相對運動方向顯式約束的導引律。該導引律在新的建模方法的基礎上，控制的目標是保持彈目相對距離和彈目相對速度的矢量方向為預先設定的理想視線方向。這種控制方式只對垂直于理想視線方向上的導彈運動進行控制，使得終端角度約束導引律形式更加簡潔。為避免彈道成型設計面臨的末端過載需求過大的問題，本文采用了過載分配優(yōu)化設計［14］，使末端彈道過載需求更小，具有更好的工程利用價值。

1 彈目相對運動學模型

為了使模型簡化便于線性二次型控制理論的應用，做如下假設:

1)導彈和目標均看作質(zhì)點運動;

2)導彈和目標的速度為常值;

3)制導系統(tǒng)是理想的，即制導控制系統(tǒng)沒有延遲，導彈的運動每一瞬間都符合導引律的要求。

在二維運動情況下，導彈和目標的相對運動關系如圖1所示。

圖1 彈目相對運動示意圖Fig.1 Engagement geometry of missile and target

圖1中:OXY 為慣性坐標系，以發(fā)射時刻導彈位置為原點，X 軸為發(fā)射時刻視線在水平面上的投影，Y 軸沿高度方向;M 為導彈位置;T 為目標;L 為理想視線;R 為彈目相對距離;v 為彈目相對速度;R⊥為R 在垂直于L 方向上的投影;v⊥為v 在垂直于L 方向上的投影。

根據(jù)圖1可以建立彈目相對運動學方程:

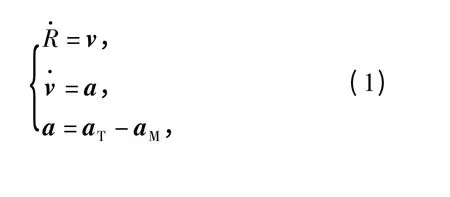
式中:a 為彈目相對加速度;aT為目標加速度;aM為導彈加速度。

將矢量R、v、a 在理想視線L 上進行投影。設L對應的單位向量為i，則沿L 方向的投影為

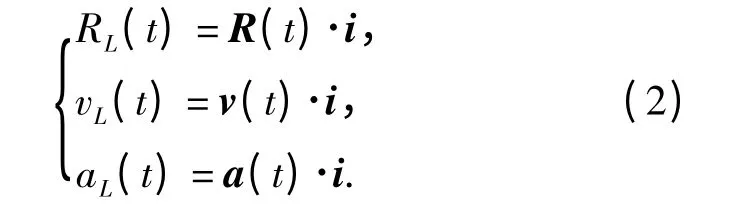
垂直于L 方向的分量為

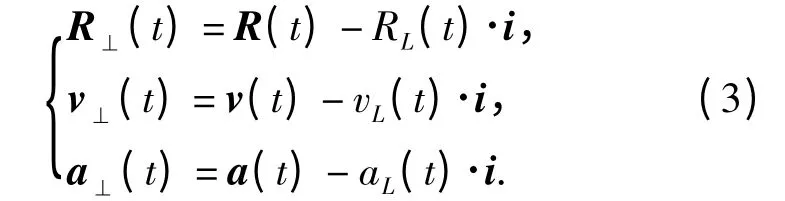
設x1=R⊥，x2=v⊥，則可建立垂直于L 方向的彈目相對運動方程:

2 彈道成型導引律

在建模完成的基礎上，可以利用最優(yōu)控制理論［15］對推導導引律，控制目標期望終端時刻彈目相對位置和相對速度處于理想視線L 上，即要求終端時刻相對位置分量x1(tf)和相對速度分量x2(tf)為0，并且希望對飛行中的過載進行合理的分配，以使過載盡可能地集中在飛行的初段，避免中末制導交接段出現(xiàn)大的過載需求，所以選取性能指標如(5)式:

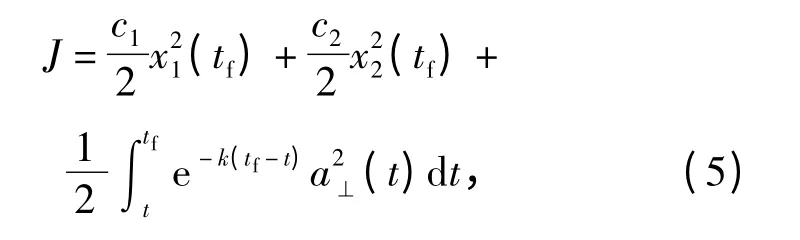
式中:c1、c2為終端狀態(tài)加權系數(shù);k 為過載分配加權系數(shù);tf為終端時間。下面根據(jù)系統(tǒng)狀態(tài)方程和指標泛函，應用最優(yōu)控制理論求解使J 最小的控制量a⊥.

2.1 推導過程

構造哈密頓函數(shù):

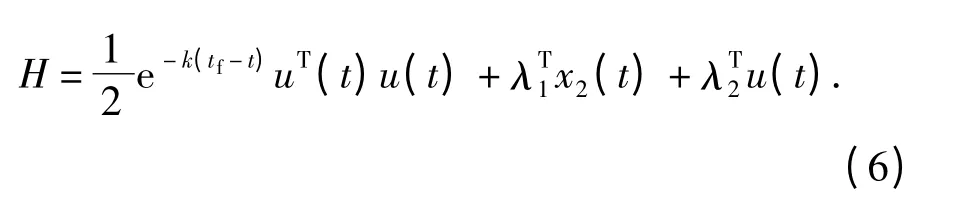
得到

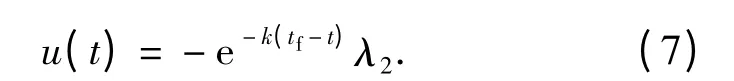
構造伴隨方程:

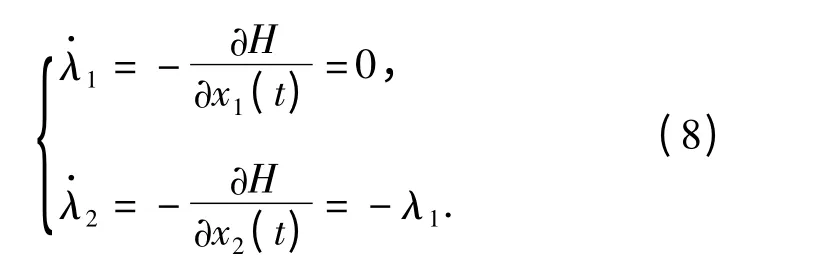
邊界條件為

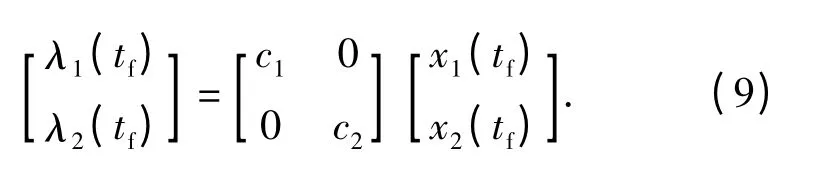
由(8)式可以解出λ1(t)和λ2(t):

將(10)式代人(7)式可得

將(11)式代入狀態(tài)方程并從t 到tf進行積分，可將u(t)改寫為

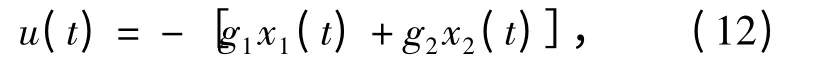
式中:

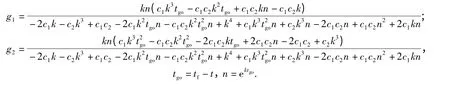
2.2 結果分析

從(12)式可以看出，u(t)不僅僅是v(t)、R(t)和剩余時間tgo的函數(shù)，還是待定常數(shù)c1、c2的函數(shù)。c1、c2選擇不同的值，可以得到不同的導引律。因要求導彈終端狀態(tài)x1(tf)和x2(tf)都盡可能小，故設c1→∞，c2→∞，并將其代入(12)式，可得

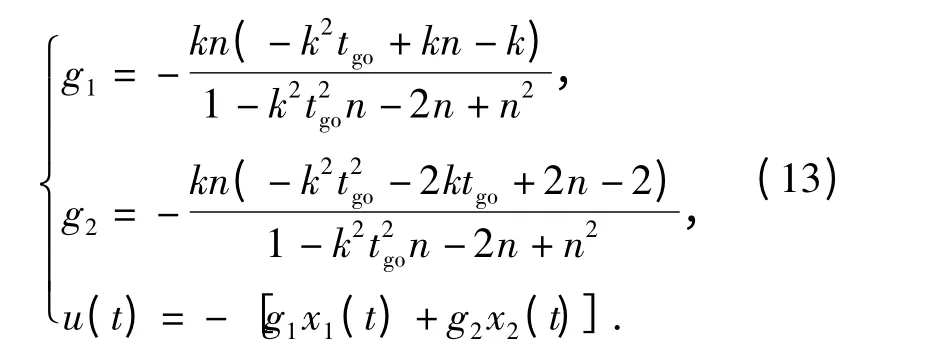
(13)式就是彈道成型最優(yōu)導引律，若取k =0，則可進一步簡化為

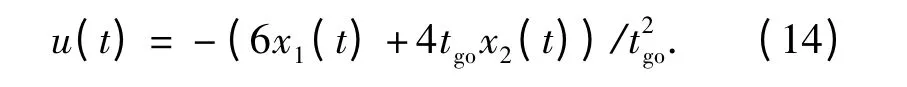
這與采用一般建模方法［4-5］的無過載約束的彈道成型導引律形式是一致的，但其中參數(shù)變量的物理意義是不同的。

3 攻擊低空下視目標制導策略設計

利用第2 節(jié)推導的彈道成型最優(yōu)導引律，可進行彈道成型中制導策略設計。

構造理想視線單位方向矢量

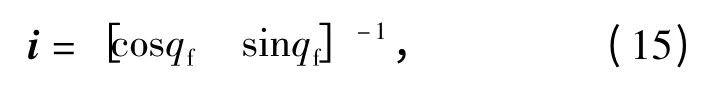
式中:qf為終端抬頭攻擊角度，其值可根據(jù)導引頭的視場角范圍確定，以保證地雜波不易落入導引頭的視場內(nèi)。

計算相對位置和相對速度在垂直于最優(yōu)終端方向上的分量:

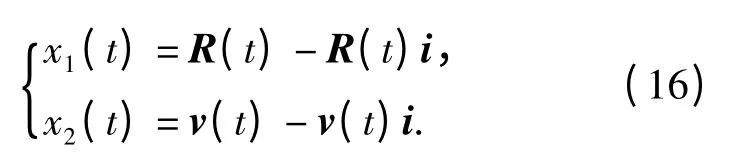
剩余飛行時間計算如下:

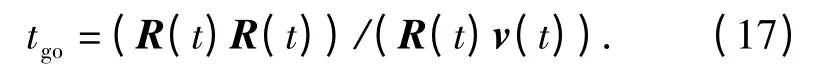
中制導段的制導指令計算如下:

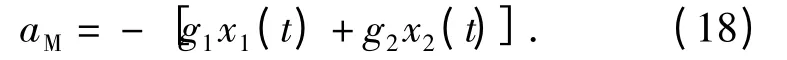
導彈轉(zhuǎn)入未制導后，采用比例導引律進行制導，制導指令為

式中:N 為有效導航比;v 為彈目相對速度;q 為視線角;q·為視線角變化率。

4 仿真分析

下面針對所設計的制導策略，建立制導系統(tǒng)平面仿真模型，并進行了制導系統(tǒng)數(shù)字仿真驗證。

仿真時導彈和目標在同一鉛垂平面內(nèi)運動，目標沿水平方向勻速直線運動。導彈的初始位置為(0，10 000 m)，初始速度為240 m/s，速度傾角為0°.目標的位置為(20 000 m，5 000 m)速度為100 m/s，速度傾角為0°.取理想視線角qf為10°、20°、30°，加速度加權系數(shù)分別取0、0.05、0.1.仿真結果如圖2～圖4所示。圖2表示在理想視線角為20°的情況下，不同加速度加權系數(shù)k 下的彈道曲線。圖3表示當理想視線角為20°時，不同的加速度加權系數(shù)所產(chǎn)生的過載曲線。圖4表示在同一個加權系數(shù)不同的理想視線角要求的情況下，仿真得到的實際視線角結果。

從仿真結果可以看出，導彈在中制導段以理想視線為基準調(diào)整飛行航跡，在中制導末端達到要求的攻擊角度。導引頭截獲目標后按比例導引律以設定的攻擊角度對目標進行攻擊。

通過修改加權系數(shù)k，可對過載進行分配。當k取0 時，表示不對過載進行分配，此時交接班過載需求較大。當k 取值越大，表示過載集中分配在彈道的初始段，從而降低了末端彈道的過載需求。

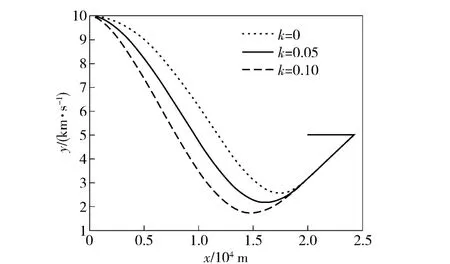
圖2 彈道曲線(qf =20°)Fig.2 Trajectories of missiles (qf =20°)

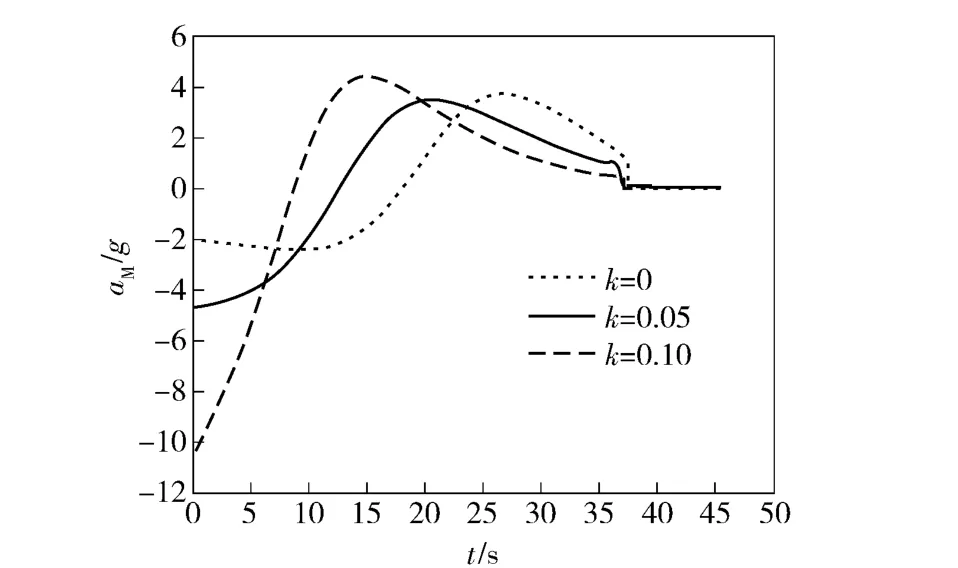
圖3 過載曲線(qf =20°)Fig.3 Accelerations of missiles (qf =20°)

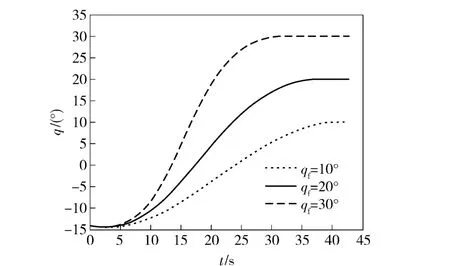
圖4 視線角曲線(k=0.05)Fig.4 Line-of-sight angles of missiles(k=0.05)

5 結論

本文針對終端彈目相對運動方向的角度約束和彈道加速度的分配需求，以理想視線為控制目標，設計了彈道成型過載優(yōu)化導引律。并以低空下視攻擊彈道為例進行了制導策略設計和數(shù)字仿真驗證，仿真結果表明:該導引律在實現(xiàn)終端運動方向約束的同時，改善了飛行過程中的過載分配問題，可有效地減小地面背景和地雜波干擾對導彈截獲跟蹤的影響，在工程上有一定的應用參考價值。而理想視線信息的準確獲取還需要進一步開展研究。

References)

［1］ 蔡洪，胡正東，曹淵.具有終端角度約束的導引律綜述［J］.宇航學報，2010，31(2):315 -323.CAI Hong，HU Zheng-dong，CAO Yuan.A survey of guidance law with terminal impact angle contraints［J］.Journal of Astronautics，2010，31(2):315 -323.(in Chinese)

［2］ Kim M，Grider K V.Terminal guidance for impact attitude angle constrained flight trajectories［J］.IEEE Transactions on Aerospace and Eletronic Systems，1973，AES-9(6):852 -859.

［3］ Idan M，Golan O M，Guelman M.Optimal planar interception with terminal constraint［J］.Journal of Guidance，Control，and Dynamics，1995，18(6):1078 -1083.

［4］ Song T L，Shin S J，Cho H.Impact angle control for planar engagements［J］.IEEE Transactions on Aerospace and Electronic Systems，1999，35(4):1439 -1444.

［5］ Shaferman V，Shima T.Linear quadratic guidance laws for imposing a terminal intercept angle［J］.Journal of Guidance，Control，and Dynamics，2008，31(5):1400 -1412.

［6］ Lee J I，Jeon I S，Tahk M J.Guidance law to control impact time and angle［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43(1):301 -310.

［7］ Taub I，Shima T.Intercept angle missile guidance under timevarying acceleration bounds［J］.Journal of Guidance，Control，and Dynamics，2013，36(3):686 -699.

［8］ Kim B S，Lee J G，Han H S.Biased PNC law for impact with angular constraint［J］.IEEE Transactions on Aerospace and Electronic Systems，1998，34(1):277 -288.

［9］ Kim T H，Park B G，Tahk M J.Bias-shaping method for biased proportional navigation with terminal-angle constraint［J］.Journal of Guidance，Control，and Dynamics，2013，36(6):1810 -1816.

［10］ Erer K S，Merttop?uoglu O.Indirect impact-ingle-control against stationary targets using biased pure proportional navigation［J］.Journal of Guidance，Control，and Dynamics，2012，35(2):700 -704.

［11］ Ratnoo A，Ghose D.Impact angle constrained interception of stationary targets［J］.Journal of Guidance，Control，and Dynamics，2008，31(6):1817 -1822.

［12］ Ratnoo A，Ghose D.Impact angle guidance against nonstationary nonmaneuvering targets［J］.Journal of Guidance，Control，and Dynamics，2010，32(1):269 -275.

［13］ Zhou D，Qu P P，Sun S.A guidance law with terminal impact angle constraint accounting for missile autopilot［J］.Journal of Dynamic Systems Measurement and Control-Transactions of the ASME，2013，135(5):DS-12 -1144.

［14］ Ben-Asher J Z，Levinson S.New proportional navigation law for ground-to-air systems［J］.Journal of Guidance，Control，and Dynamics，2003，26(5):822 -825.

［15］ 張洪鋮，王青.最優(yōu)控制理論與應用［M］.北京:高等教育出版社，2006:31 -63.ZHANG Hong-cheng，WANG Qing.Optimal control theory and application［M］.Beijing:Higher Education Press，2006:31 -63.(in Chinese)