基于支持度矩陣的關聯規則挖掘算法在公安情報分析中的應用*

李為 王池 重慶市公安局巴南分局

基于支持度矩陣的關聯規則挖掘算法在公安情報分析中的應用*

李為 王池 重慶市公安局巴南分局

將關聯規則算法引入公安情報的數據挖掘中，以求發現情報信息中的相關規律，提高執法效率與快速反應能力，并及時預防和打擊犯罪行為。由于關聯規則Apriori算法存在多次掃描數據庫并且時間性能較低的缺陷，提出了一種基于矩陣的關聯規則挖掘算法。該算法通過對矩陣操作，只需掃描數據庫一次，就能一次產生所有頻繁項集，大大減少了計算項集的工作，有效提高了挖掘效率。

數據挖掘 頻繁項集 支持度矩陣 Apriori算法

一、引言

隨著現代科學技術的發展、科技強警的不斷推進，全國公安機關依托“金盾工程”進行了一場公安信息化的現代警務新變革，公安信息化系統建設已成為打擊違法犯罪活動的有力工具，但在實際工作中收集和積累的海量社會信息和數據信息越來越多、數據規模日益增大、復雜程度不斷增加已成為公安信息系統處理的難題[1]。為了適應信息動態管理，如何從這些蘊涵大量有用情報的信息數據中及時發現、總結各種犯罪的規律性、最新規則以及社會治安的變化特點，以制定有利于社會穩定和發展的決策，提高執法效率與快速反應能力，及時預防和打擊犯罪行為，并采取相應的措施顯得越來越重要。將數據挖掘技術應用于公安情報分析，能夠為公安部門提供各種決策信息以及解決方案，大大提高決策的質量和效率，已成為當前公安工作中亟需進一步研究解決的問題，也是公安信息化建設進一步發展的方向。

在絕大多數犯罪活動中，犯罪活動之間或內部擁有錯綜復雜的聯系，犯罪數據挖掘得到了很大關注，各種數據挖掘技術的研究為社會安全提供了幫助[2]。現有關聯規則數據挖掘算法[3]已不太適應當前公安信息系統的發展。針對在關聯規則挖掘中如何高效挖掘頻繁項集，本文提出了生成支持度矩陣并利用矩陣理論的頻繁項集挖掘算法。該算法通過對矩陣操作，只需掃描數據庫一次，就能一次產生所有頻繁項集，大大減少了計算項集的工作，有效提高了挖掘效率。

二、基于矩陣的關聯規則信息挖掘高效算法

（一）關聯規則的基本概念及定義

關聯規則是描述數據庫中數據項之間存在的潛在關系的規則，即反映一個事物與其它事物之間的相互依存性和關聯性。問題可以描述如下[4]：I={i1,i2,...,im}由m個不同項組成，是所有項的集合；D={T1,T2,...,Tn}由一系列具有唯一標識TID的事物組成，是所有事物的集合。每個事物T由I中的若干項組成，是I的子集，記為T={t1,t2,...tn}，t1I。若X、Y是數據項集，X中含有的項數目為k，則稱為k-項集。事物集D中的關聯規則表示為蘊涵式X Y，且X I，Y I，X∩Y=φ，X為規則的前提，Y是結果。

給定一個事物集D，挖掘關聯規則就是產生支持度和置信度分別大于用戶給定的最小支持度（min_supp）和最小置信度（min_conf）的關聯規則。當規則的置信度和支持度分別大于min_supp、min_conf時，我們認為規則是有效的，稱為強關聯規則。當數據項集X的支持度大于min_supp時，稱X為高頻數據項集。

定義1項的向量表示：

Ii則項Ii相應的支持度表示為

cup_count[Ii]=（Ii表示項，j表示事物標號）。

定義2項集I的矩陣記為：

定義3k-項集的支持度計數：

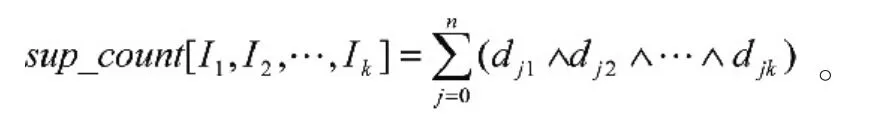
定義4關聯規則的置信度：

性質1一個頻繁項集的任一子集必定是頻繁項集。

性質2一個非頻繁項集的任一超集也是非頻繁項集。

（二）基于矩陣的關聯規則挖掘算法

算法的具體實現過程描述如下：

1. 把事物數據庫構造成矩陣，求頻繁1-項集

對給定的事務數據庫D，根據定義2構造矩陣M1。以事物表示成行向量，項表示成列向量，若第i個事物中包含了第j個項，則矩陣的第i行第j列的值為1，否則值為0。該矩陣中的每一個位置在內存中僅占一位。

對該矩陣各列向量掃描，根據定義1，由矩陣的各列數字和就可以得到支持度計數。當支持度計數sup_count[Ii]>min_supp，則Ii為頻繁項，將該項加入頻繁1-項集L1中。否則Ii非頻繁項集，將其從事務矩陣中刪除。

2. 構造二項集的支持度矩陣，快速找出頻繁2-項集

由頻繁1-項集構造|L1|階2-項集支持度矩陣M2，此矩陣為對稱矩陣。根據定義3，依次求出矩陣中各元素對應的2-項集支持度計數。當M2[i,j]=mis_supp(imin_supp，則M2[i,j]為頻繁項，將該項加入頻繁2-項集L2中。否則M2[i,j]為非頻繁項集，不加入頻繁項集中。

3. 利用支持度矩陣，尋找所有頻繁項目集

對于每個候選k（k≥3）項集X，從X在Ck之后的位置中查找以X后k-1個項開始的其它候選k項集，若找到這樣一個候選k項集Y，則把X的第一個項Ir和Y的最后一個項Is的標號連接形成矩陣坐標[r,s]，到矩陣M2中查找這個坐標上的值是否大于最小支持度計數min_supp，如果大于或等于，則生成候選k+1項集；如果不大于，則不予連接，繼續查找下一個，直到Ck中的最后一個k項集。至此候選k+1項集表構造結束。

4. 由頻繁項集產生關聯規則

從事物數據庫D中挖掘出所有的頻繁項集后，就可以產生關聯規則，即產生滿足最小支持度和最小置信度的強關聯規則。根據定義4中的公式，具體產生關聯規則的操作如下：

（1）對于找出的每個頻繁項集l，產生l的所有非空子集s；

（2）對于每個非空子集s，如果包含l的事務數與包含s的事務數的比值大于最小置信度，即support(l) /support(s)≥min_conf，則輸出規則“s l-s”，其中min_conf是最小置信度。

由于關聯規則是通過頻繁項集直接產生的，因此關聯規則所涉及的所有項集均滿足最小支持度。

（三）算法在公安情報分析中的應用

選取少量登記在案的犯罪嫌疑人員數據，由此算法進行數據挖掘。假定T1～T10為案件編號，a～f分別為案件相關信息，則案件與事件信息之間的關系如表1所示，假設最小支持度計數為4。

?

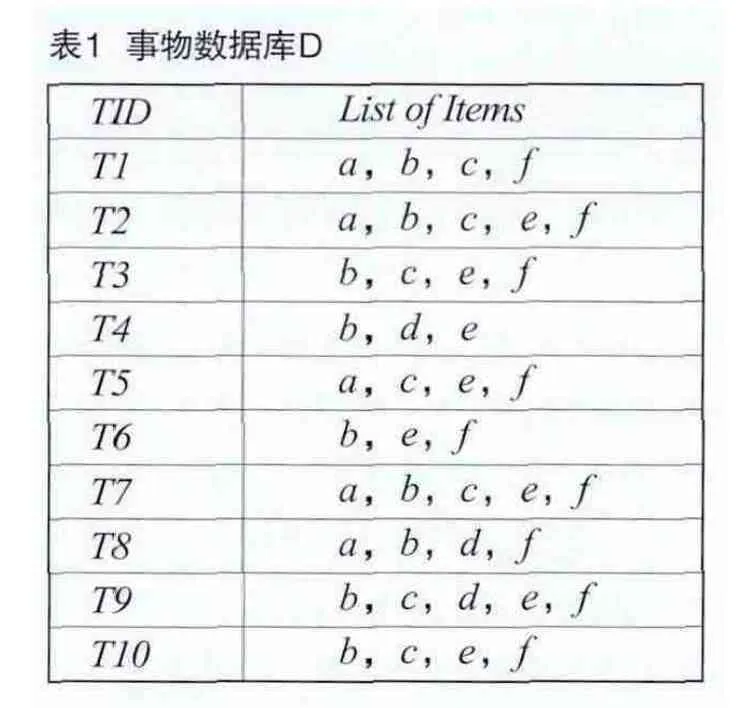
（1）掃描數據庫，得到事物矩陣M1。

（2）構造支持度矩陣M2。

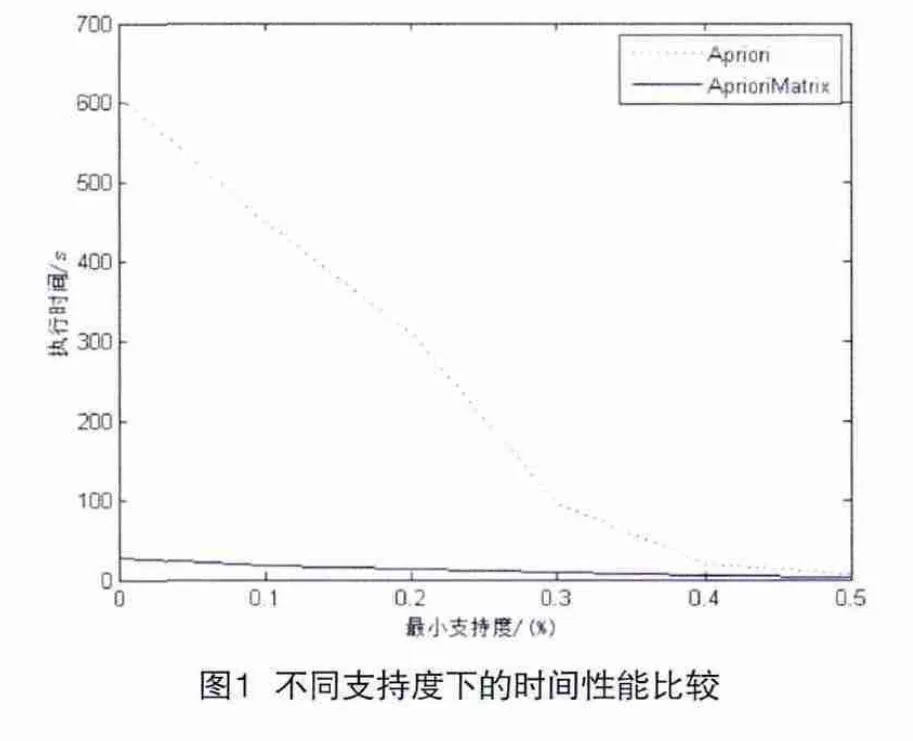
根據定義3，依次求出M2[i,j](i

?

把M2中元素與最小支持度min_supp=4比較，得到頻繁2-項集L2={{a，b}，{b，c}，{a，c}，{c，e}，{b，e}，{e，f}，{c，f}，{b，f}，{a，f}}。

（3）對a行的二項集進行掃描，發現二項集{a，b}大于最小支持度，于是轉到b行，搜索b行中大于最小支持度計數的二項集，得到{b，c}，{b，e}，{b，f}。然后定位到矩陣[a，c][a，e][a，f]，發現M2[a,e]k，則{a，b，f}一定不是頻繁3-項集。然后繼續對a行后面的頻繁二項集進行查找工作，當a行搜索完畢后，對后面的行進行掃描。用此方法依次搜索，可求出頻繁3-項集L3={{b，c，e}，{b，e，f}，{c，e，f}，{a，c，f}，{b，c，f}，{a，b，f}}。

（4）發現候選4-項集以及更高維的k項集，對于三項集{b，c，e}，從它的位置之后在C3中查找以{c，e} 開頭的其它三項集，發現符合條件的三項集{c，e，f}，于是定位到矩陣坐標[b，f]中，發現{b，f} 是頻繁2-項集。于是生成候選四項集{b，c，e，f}，此時已不能再生成其它候選四項集以及更高維的k項集，生成k項集表的連接剪枝過程至此結束。L4為{{b，c，e，f}}。

三、實驗結果分析

（一）與Apriori算法的比較

1. 時間復雜性

Apriori算法是逐層搜索的迭代算法，通過頻繁（k-1） -項集搜索頻繁k-項集。其時間復雜度為其中xx為交易事務數據庫中包含的交易數量，k為頻繁項集大小。Apriori算法在挖掘每一層中所包含的頻繁項目集時都需要進行一次數據庫掃描，來獲得候選項集的支持度。而且在發現頻繁項目集的過程中，產生了大量的候選項目集。當遇到海量數據庫時，耗時太長，難以滿足實際應用的需求。同時Apriori算法的效率不高，利用頻繁（k-1）-項集連接產生候選k-項集，判斷連接條件時重復次數太多[5]。

而本文算法中只需要一次掃描數據庫得出事務矩陣，并求出支持度，構造二項集的支持度矩陣。根據支持度矩陣的性質產生頻繁k-項集。利用矩陣可以更方便地處理數據，減少候選項集的生成，大大地提高了挖掘關聯規則的效率，并且基于矩陣的算法也便于在實際應用中被實現和理解。

2. 空間復雜性

Apriori算法會產生大量的候選項集，并且所有具有相同長度的候選項集必須被存儲在內存中，這將會占用大量的內存空間，導致內存不停地換進換出操作。而本文算法采用矩陣進行存儲，大量減少所需的I/O次數，減小了存儲空間，不需要在內存中存儲所有的候選項集，具有良好的空間特性。

（二）實驗結果分析

為了對算法的優勢進行驗證，將其進行實驗驗證。在Inter(R) Core(TM) i3 CPU 2.27GHz，4.00GB內存，Windows 7 64Bit操作系統的實驗環境下，算法采用Java語言實現。實驗數據采用T40I10D100K，將本文所述的優化算法與Apriori算法進行比較。圖1是在最小支持度不同時，挖掘所有頻繁項集執行時間的區別。由圖1可知，Apriori算法當支持度減少時，耗費的時間會增大，而本文算法受最小支持度的影響較小；并且當最小支持度越小時，優化后算法的執行時間比Apriori算法的執行時間少得越多，這說明優化后的算法在給出支持度較小時具有較高的執行效率。

圖2給出了當數據庫中事務記錄數不同時兩種算法執行時間的區別。由圖2可知，兩種算法執行時間都會呈上升趨勢，但當事物記錄適當大時，優化后算法的效率比Apriori算法的效率要高一些，這說明優化后的算法在所給數據庫中記錄較大時具有較高的執行效率。

四、結束語

關聯分析是數據挖掘技術的一個重要的應用。基于經典的關聯規則發現算法Apriori算法的研究，提出了改進的基于支持度矩陣的關聯規則發現算法：該算法僅掃描數據庫一次，把結果存儲到矩陣中，節省了大量的內存空間，并通過矩陣運算來計算項的支持度計數，并生產支持度矩陣來產生頻繁項集。將該算法應用到公安情報分析領域的規則發現中，通過對案件信息的一些強關聯規則的挖掘，為公安偵破工作提供依據，提高了決策的質量和效率。

[1] 趙偉.數據挖掘技術在公安預測預警中的應用[J].警察技術,2009,9:56-58.

[2] Chen H,Chung W,Jie J,et al.Crime Data Mining:A General Framework and Some Examples[J].The IEEE Computer Society,2004.

[3] Patel Nimisha R,Sheetal Mehta.A Survey on Mining Algorithms[J].International Journal of Soft Computering and Engineering(IJSCE),2013.

[4] Jiawei Han, Micheline Kamber. 數據挖掘概念與技術[M].機械工業出版社,2001.

[5] 倪堅.對Apriori算法的一個改進[J].大連交通大學學

公安理論及軟科學研究計劃（編號：20125000000000871）