Laplace變換求解成層土中污染物一維擴散問題

余 闖，溫燦燦，陳樟龍，蔡曉慶，劉俊峰

（溫州大學a.建筑與土木工程學院；b.數學與信息科學學院，浙江 溫州 325035）

Laplace變換求解成層土中污染物一維擴散問題

余 闖a，b，溫燦燦b，陳樟龍a，蔡曉慶a，劉俊峰b

（溫州大學a.建筑與土木工程學院；b.數學與信息科學學院，浙江 溫州 325035）

成層土中污染物的遷移規律較為復雜，將其簡化為一維擴散模型。運用Laplace變換和Laplace數值逆變換方法進行了求解，編制了計算程序。計算結果可以退化到單層土的情況，結論與經典的理論解完全一致。通過與現有用數值軟件計算結果的對比，檢驗了解答的正確性；采用的計算方法對一室內試驗結果進行了模擬，計算結果和實測數據較為吻合，證明所提方法的可靠性。求解方法可用于求解更為復雜的邊界條件下的污染物遷移問題。

污染物擴散；成層土；Laplace變換；一維擴散模型

污染物在土層中的擴散問題一直是學術界研究的熱點問題。近年來，國外學者對垃圾填埋場中污染物的遷移模型做了大量的研究工作，但在中國，關于這方面的研究還不多［1－4］。

污染物在土介質中的遷移規律受很多因素的影響［5－6］，主要有：對流、彌散、分子擴散、蛻變及吸附等。一般認為同時考慮對流、彌散和蛻變項的遷移模型［7－9］能較好地反映實際情況，但是模型的求解難度也隨考慮因素的增加而加大。Rowe等［10－11］用數值變換的方法求解了成層土中自由上邊界條件和底部有潛水層的下邊界條件下污染物的遷移問題。楊文參等［12］利用分離變量法求解成層土中的污染物擴散問題，但由于分離變量法所要求齊次邊界條件的限制，很難處理邊界條件復雜的問題。然而，實際邊界條件往往較為復雜［11］，這就需要有處理更加復雜邊界條件的數學工具。本文運用Laplace變換和Laplace數值逆變換求解成層土中污染物一維擴散模型，模型邊界條件相對簡單，目的是對該問題進行初步研究，檢驗所提方法的可靠性，以便進一步深入分析研究。

1 污染物擴散模型

求解成層土中污染物一維擴散模型主要基于以下假設：1）成層土為均質、飽和的；2）第i層土介質中阻滯因子和有效擴散系數是常數，不隨時間、空間變化；3）污染物的擴散是一維的，并且污染物源在土層上部，不考慮其他的外部污染源；4）污染物的擴散僅有污染物的溶度梯度引起，忽略水力傳導的作用，同時考慮土顆粒對污染物的線性吸附作用。

在上述基本假設的前提下，簡化污染物在土壤中的遷移方程［2］，得到了成層土中污染物的一維擴散模型，如圖1所示。對于成層土中第i層，污染物的擴散方程為

式中：Ci為第i層土中的污染物濃度；Ri為第i層土對污染物的阻滯因子；Di為第i層土中污染物擴散的擴散系數。

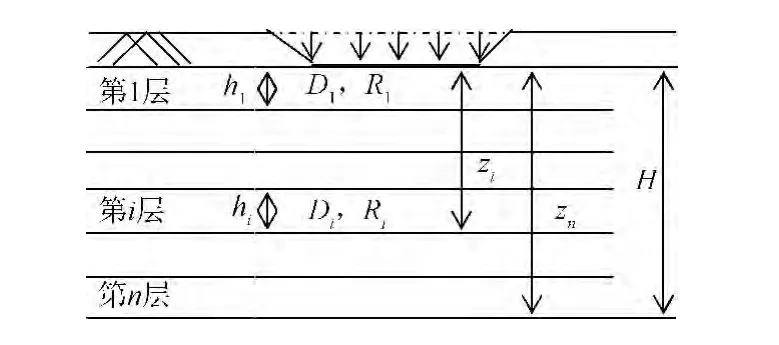
圖1 污染物一維擴散剖面圖

2 模型求解

由于式（1）類似于Terzaghi一維固結方程，故參考文獻［13］的求解方法，對式（1）進行Laplace變換：

由于式（18）很難通過Laplace逆變換得到時域解析解，故采用數值Laplace逆變換方法［14］求解。

3 模型驗證分析

3.1 退化為單層解的情況

當上述解退化為單層土層時，式（17）可簡化為：

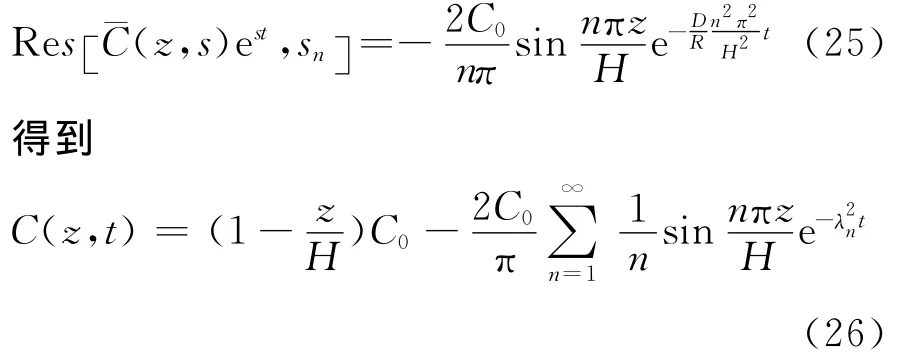
方程（26）即為文獻［9］中退化為單層土的解答。

3.2 與已有成層解答對比

基于上述Laplace逆變換解答，筆者編制了相應的計算程序。對于層狀土中污染物的一維擴散解析解，文獻［12］假設了兩層介質的物理化學性質如表1所示，邊界條件為頂部濃度為1.0（常濃度），底部為0。同時采用著名的污染物分析軟件GAEA Pollute V7進行了計算，如圖2所示，兩者所獲得的結果基本保持一致，從而說明本文解答及所編寫程序的可靠性。

表1 土層的物理化學性質參數

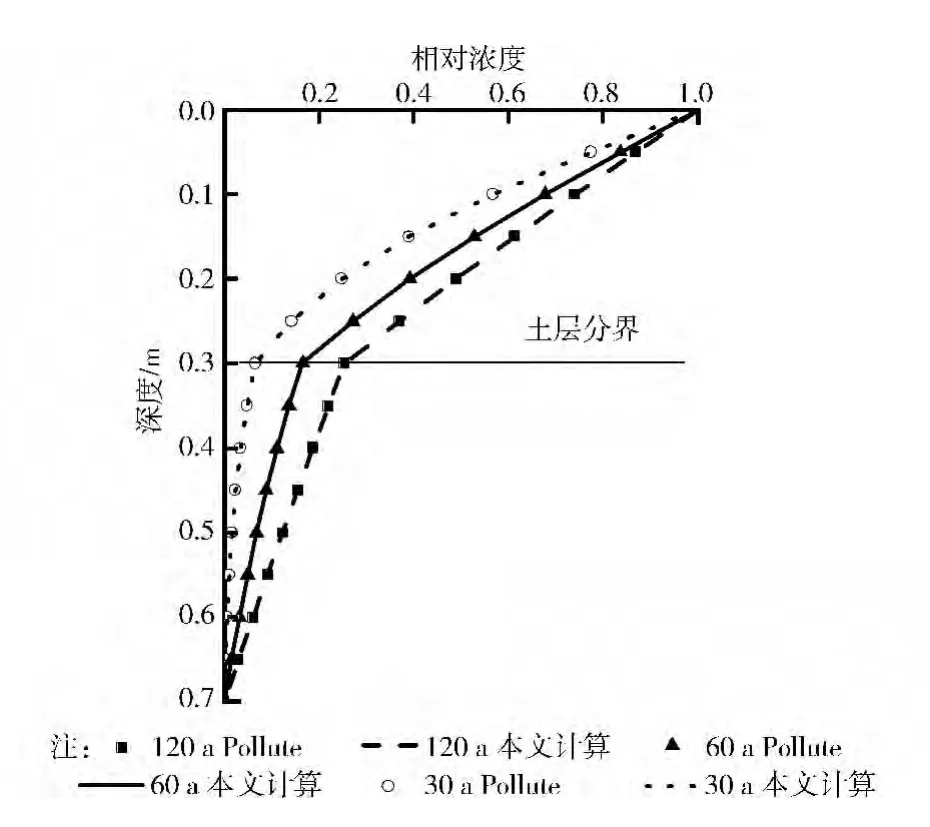
圖2 理論計算與數值分析結果對比

3.3 實驗數據計算分析

Roehl等［15］設計了室內一維擴散模型，分析了常濃度條件下Cd2＋在粘土中的遷移規律。粘土層厚度5 cm，比重1.68 g／cm3，含水量17.5%，試驗溫度控制在20±8℃，分別測試了43 d到520 d中5個時間段、不同深度處的Cd2＋濃度。粘土擴散系數D為6.5×10－8cm2／s，阻滯因子R 為35，計算結果和模型試驗結果對比如圖3所示。由此可見，計算結果和實測數據比較一致。

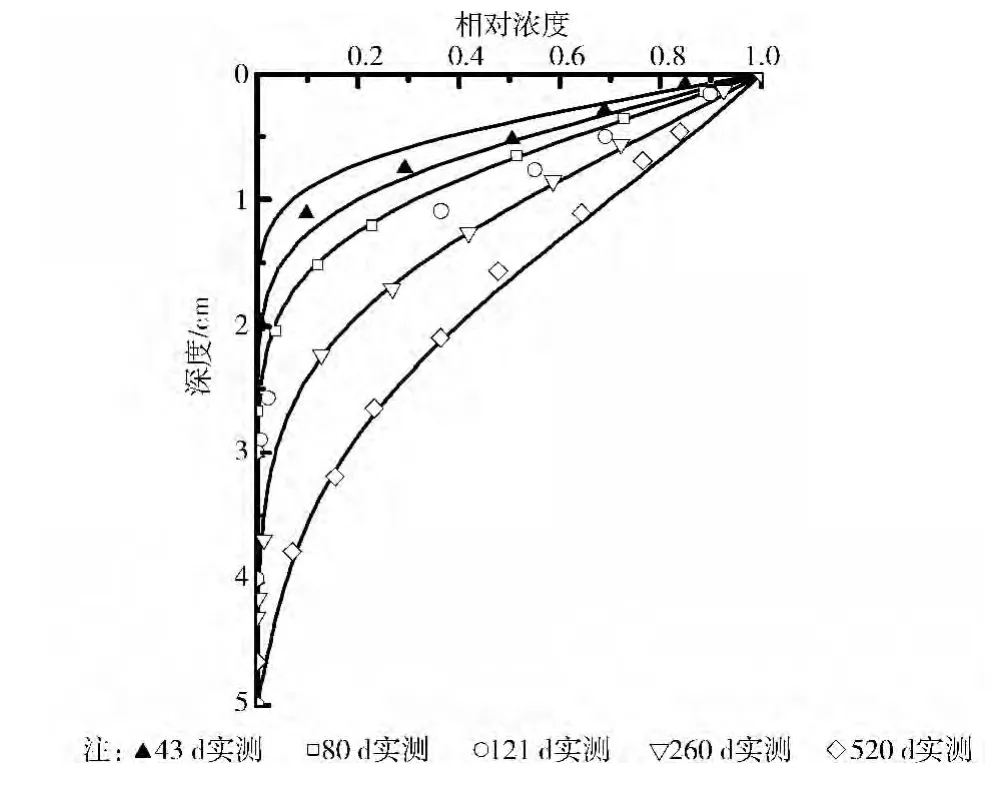
圖3 理論計算與模型試驗結果對比

4 結論

成層土中污染物的遷移規律較為復雜，將其簡化為一維擴散模型，運用Laplace變換和Laplace數值逆變換方法進行了求解，編制了計算程序。計算結果可以退化到單層土的情況，所得結論與經典的理論解完全一致。通過與現有用數值軟件GAEA Pollute V7計算結果的對比，兩者計算結果保持一致，檢驗了解答的正確性；采用計算方法對一室內Cd2＋在粘土中擴散試驗進行了模擬，計算結果和實測數據較為吻合，證明所提方法的可靠性。

［1］崔振東，唐益群.地下水流與水質聯合數值模擬應用研究［J］.土木建筑與環境工程，2009，31（1）：120-124.

Cui Z D，Tang Y Q.Numerical simulation of groundwater flow and quality ［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2009，31（1）：120-124.

［2］杜延軍，金飛，劉松玉，等.重金屬工業污染場地固化／穩定處理研究進展［J］.巖土力學，2011，32（1）：116-124.

Du Y J，Jin F，Liu S Y.Review of stabilization／solidification technique for remediation of heavy metals contaminated lands［J］.Rock and Soil Mechanics，2011，（1）：116-124.

［3］席永慧，劉建航.飽和多孔介質中污染物遷移模擬［J］.同濟大學學報：自然科學版，2005，33（5）：644-648.

Xi Y H，Liu J H.Modeling of contaminant migration in saturated porous media［J］.Journal of Tongji University：Natural Science，2005，33（5）：644-648.

［4］查甫生，許龍，崔可銳.水泥固化重金屬污染土的強度特性試驗研究［J］.巖土力學，2012，33（3）：652-657.

Zha F S，Xu L，Cui K R.Strength characteristics of heavy metal contaminated soils stabilized／solidified by cement［J］.Rock and Soil Mechanics，2012，33（3）：652-657.

［5］付國楷，張馳，張智，等.污染物在人工復合生態床中的遷移轉化途徑［J］.土木建筑與環境工程，2010，32（2）：122-127.

Fu G K，Zhang C，Zhang Z.Transportation and transformation of pollutants in a new type constructed wetland［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2010，32（2）：122-127.

［6］Mathur S，Jayawardena L P.Modelling migration of contaminants from waste disposal facility［J］.International Journal of Environmental Studies，2005，62（1）：15-34.

［7］Rowe R K，Booker J R.A finite layer technique for modeling complex landfill history［J］.Canadian Geotechnical Journal，1995，32：660-676.

［8］Rabideau A J，Khandelwal A.Boundary conditions for modeling transport in vertical barriers［J］.Journal of Environmental Engineering，1998，124（11）：1135-1139.

［9］Jury W A，Spencer W F，Farmerm W J.Behavior assessment model for trace organics in soils ［J］.I.Model description［J］.J.Environ.Qual.，1983，12（4）：558-564.

［10］Rowe R K，Booker J R.The analysis of pollutant migration in a non-homogeneous soil［J］.Geotechnoque，1984，4：601-612.

［11］Rowe R K，Booker J R.Clayey barrier system for waste disposal facilities［M］.London：E ＆FN Spoon，1995.

［12］楊文參，謝海建，陳云敏.考慮降解時污染物在底泥及覆蓋層中的運移解［J］.土木工程學報，2011，44（Sup 2）：181-185.

Yang W C，Xie H J，Chen Y M.Analytical solution for contaminant transport through underwater soil and overlying cap layer considering degradation ［J］.China Civil Engineering Journal，2011，44（Sup 2）：181-185.

［13］徐長節，蔡袁強，吳世明.任意荷載下成層彈性地基的一維固結［J］.土木工程學報，1995，17（5）：80-85.

Xu C J，Cai Y Q，Wu S M.One dimensional consolidation of layered elastic soils under arbitrary loading ［J］.China Civil Engineering Journal，1995，17（5）：80-85.

［14］Durbin J W.Numerical inversion of Laplace transforms：an efficient improvent to Duber and Abate's method ［J］.Comput Journal，1973，17（4）：371-376.

［15］Roehl K E，Czurda K.Diffusion and solid speciation of Cd and Pb in clay liners ［J］.Applied Clay Science，1998，12：387-402.

（編輯 胡 玲）

Solution for One-Dimensional Contaminant Diffusion in Layered Clayey Soils Using Laplace Transforms

Yu Chuanga，b，Wen Cancanb，Chen Zhanglonga，Cai Xiaoqinga，Liu Junfengb

（a.College of Architecture and Civil Engineering；b.College of Mathematics ＆Information Science，Wenzhou University，Wenzhou 325035，Zhejiang，P.R.China）

Contaminant diffusion in layered soil is very complex.The diffusion process is simplified as a onedimensional diffusion mode.The Laplace transformation and Laplace numerical inverse transformation are adopted.The proposed solution can be degraded to a single layer case.The obtained results are well consistent with those obtained by the classic theory.The correctness of the presented solution is verified by comparing the calculation results with the results generated by existing numerical software.One case study is conducted and the calculation results have a good agreement with measured data，which prove the reliability of the proposed method.The presented method can be used to solve more complex boundary conditions of contaminant migration.

contaminant migration；layered soil；laplace transformation；one-dimensional diffusion model

TU820.6

A

1674-4764（2014）02-0115-04

10.11835／j.issn.1674-4764.2014.02.018

2013-10-15

國家自然科學基金（41002091、41372264）；浙江省自然科學基金（LY13E080013）；中國博士后科學基金面上項目（2012M521851）。

余 闖（1977-），男，博士，教授，主要從事環境巖土、地基處理等研究，（E-mail）3945735＠qq.com。