基于微觀力學分析的散粒體靜力液化本構模型

劉 洋，汪成林，閆鴻翔

（1.北京科技大學 土木與環境工程學院土木系，北京 100083；2.中國公路工程咨詢集團有限公司，北京 100097）

基于微觀力學分析的散粒體靜力液化本構模型

劉 洋1，汪成林1，閆鴻翔2

（1.北京科技大學 土木與環境工程學院土木系，北京 100083；2.中國公路工程咨詢集團有限公司，北京 100097）

針對散粒體的靜力液化特性，在散粒體顆粒運動微觀力學分析的基礎上，在臨界狀態土力學框架內建立了一個簡單的靜力液化彈塑性本構模型。模型屈服函數和和硬化規律根據Chang提出的砂土微觀力學模型，通過積分粒間接觸力為宏觀的應力不變量而建立，考慮了與材料狀態相關的剪脹性和初始密度對散粒體應力 應變關系的影響，并采用非相關聯的流動法則。模型參數簡單且有較明確物理意義，可以通過室內三軸試驗確定。模型的數值結果與Toyoura砂以及砂 粉混合土的三軸不排水剪切試驗的應力 應變曲線和應力路徑吻合較好。

散粒體；靜力液化；本構模型；數值模擬

砂土等散粒體的液化包括靜荷載引起的靜力液化和地震、爆炸以及機械振動等動力荷載引起的循環液化。對于循環液化，學者們對其進行了大量的研究［1］；對于靜力液化，近幾十年間卻沒有得到足夠的關注和認識。對地基、邊坡等土工構筑物來說，靜力液化是一種常見的破壞形式，對土工問題進行靜力液化穩定性分析時，不管采取何種數值方法，首要問題是建立合理的靜力液化應力－應變關系。

散粒體（如砂土）的應力 應變模型主要有兩類：基于連續介質力學的彈塑性本構模型和基于散粒介力學分析的微觀力學模型。經典彈塑性力學模型將砂土看成連續介質，如Desai等［2］提出的帽子模型、Prevost等［3］提出的多重屈服面塑性模型以及Dafalias等［5］提出的邊界面模型等等。另外一些學者將砂土看成顆粒集合體，基于接觸力學和均一化方法提出砂土的微觀力學模型，早期的研究主要集中在砂土彈性力學行為，如Chang等［5］的工作。對彈塑性應力－應變關系的研究要復雜一些，如Jenkins等［6］、Chang等［7］、Yin 等［8］、Nicot等［9－10］、Misra等［11］、Lai等［12］、Zhang等［13］、Tran 等［14］、Shen等［15］提出的微觀力學模型。對于散粒體的靜力液化問題，也有學者提出了一些用以模擬各向同性不排水條件下砂土的靜力液化的模型（如Boukpeti等［16－17］）。

本文針對散粒體的靜力液化特性，借鑒微觀力學本構關系一些成果，在臨界狀態土力學框架內建立散粒體的靜力液化本構模型。文章首先簡要闡述了靜力液化的基本原理，接著提出了適用于散粒體的靜力液化本構模型，并對模型參數及其一般力學響應進行了分析，最后根據已有的三軸試驗結果對提出的模型進行了評價。

1 靜力液化

關于靜力液化，太沙基早在1948年首先用“自然液化”描述了非常松散的砂土在微小擾動下突然失去強度而象粘滯性流體一樣的流動現象，這里的“自然液化”即為后來 Castro等［18］和 Casagrande［19］在討論滑坡災害時提出的“靜力液化”概念。它們描述了在靜荷載條件下砂土的強度降至很低，不能再繼續承受剪切作用，可以如液體一樣流動的特性，同時也指出只有非常松散的砂土才能發生靜力液化。

從概念上靜力液化可以定義為：在單調加載過程中偏應力－應變曲線出現明顯的應變軟化現象，隨著偏應力在峰值后的急劇降低而接近零值，砂土表現出類似于流體的特征，但由于砂土未承受動荷載作用，為了與通常的振動液化區別，故稱之為“靜力液化”。

靜力液化的原理如圖1所示，τst是砂土的初始應力狀態，φcv是臨界狀態摩擦角，曲線①、②分別是單調荷載和循環荷載下的應力路徑。無論是單調荷載還是由振動產生的循環荷載，由它們產生的瞬態荷載都會使砂土產生液化。圖中可見，應力一旦超過破壞面，剪切強度就會快速下降，至到穩定狀態即殘余強度sus處。雖然單調荷載和循環荷載的應力路徑不同，但它們都具有相同的最終狀態。

圖1 飽和散粒體單調和循環加載響應

2 散粒體顆粒運動微觀力學分析

2.1 顆粒間彈性力學行為

定義散粒體顆粒間的接觸法向為垂直于接觸面的法向矢量，在每個接觸面上建立局部坐標如圖2所示。顆粒接觸法向與切向接觸剛度分別為kαn和kαr，粒間接觸力可定義為

圖2 粒間接觸處的局部坐標系

式中，n、s、t是局部坐標系中3個正交的單位法向量。設粒間接觸服從修正的Hertz-Mindlin接觸本構關系［5］：

2.2 顆粒間塑性力學行為

顆粒接觸處存在著向上或者向下的塑性滑動，這種塑性運動產生體積改變，在散粒體中稱之為剪脹／剪縮行為，粒間剪脹可用式（4）描述。

3 散粒體靜力液化宏觀本構方程

基于上述顆粒運動微觀力學分析，假設散粒體均勻，并在各向同性應力狀態下積分式（4）、（6）、（7），即得到散粒體宏觀剪脹方程、屈服函數和硬化規律。

3.1 控制方程

模型的數學表達式以應力和應變不變量的形式給出，應力不變量采用p′和q，它們分別與第一應力不變量I1和第二偏應力不變量J2相關，式中p′和I1′代表有效應力。p′和q以應力張量和偏應力張量表示為

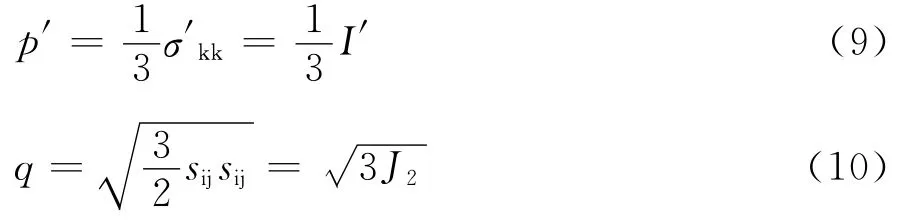
式中，偏應力張量sij＝σii－1／3σkkδij，與其相應的應變增量以應變張量和偏應變張量表示為

其中，偏應變張量eij＝εii－1／3εkkδij。假設材料各向同性，根據彈塑性理論材料變形分為彈性和塑性兩部分，即：

這里K0和是兩個材料常數，K0是參考體積模量；pref是參考壓力，一般取1個大氣壓；為指數。

上述彈性行為只發生在屈服面內，屈服準則采用摩爾－庫倫類準則

該屈服面是在Chang等［14］提出的砂土微觀力學模型的基礎上，將微觀的接觸力積分為宏觀的應力和而來。同理，根據式（7）硬化規律，采用式（19）所示雙曲線形式。

式中，Mp＝6sinφp／（3－sinφp），從物理意義上講，φp的值應等于庫倫摩擦角（φμ），但為了考慮散粒體密實度的影響，消除各向同性假設帶來的誤差，將φp看成是密實度函數，即

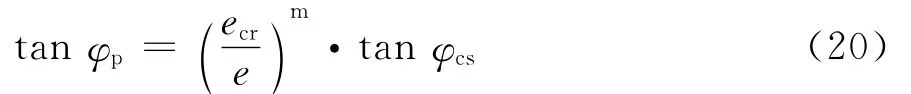
式中：m是一個與散粒體類型（特別是顆粒形狀）有關的一個正指數；φcs是臨界狀態摩擦角。對于密砂，峰值摩擦角φp大于臨界狀態摩擦角φcs，在剪應力作用下砂土剪脹，顆粒的咬合和摩擦降低，產生應變軟化行為。

這里ptm是參考大氣壓力。式（21）中的3個參數確定了e-p空間臨界狀態線（CSL）的形狀，即：eerf（CSL在e軸的截距），λ（CSL線的斜率），以及ξ（CSL的曲率）。

塑性剛度kp0與體積模量K的關系用式（22）關聯。

顯然，本文提出的模型采用了非相關聯的流動法則。

2.2 應力 應變關系

根據經典彈塑性理論，總應變增量分成兩部分，即彈性部分和塑性部分。

4 本構方程的數值積分

在積分計算前，首先假設材料響應為彈性響應，通過彈性本構關系獲得一個測試應力狀態，即：

式中，T表示應力狀態為測試應力，數值大小為當前應力狀態加上微小變形后所產生的彈性應力。如果測試應力狀態點位于屈服面所定義的彈性區域內，則有效應力分量的更新值等于測試應力。

如果測試應力狀態點位于當前屈服面外，即F（p′T，qT）＞0，則對測試應力進行修正計算，此時積分步計算分為兩個子步：求解新的應力狀態點，使其滿足屈服條件；更新屈服面位置，進行更新計算。積分步如圖3所示，圖中F代表屈服面，G代表塑性勢面。

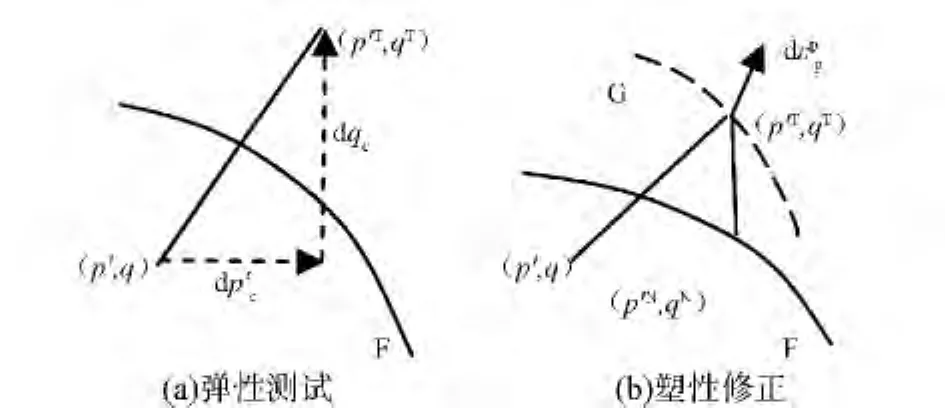
圖3 本構方程積分步的兩個子步

新的應力狀態是在彈性變形和塑性變形共同作用下達到的，如圖3（b）所示，因此需要由彈性法則和塑性應變增量共同來確定。

結合流動法則可將新的應力狀態表示為式（35）和（36），點 （p′NqN）位于屈服面上。

式（38）的求解采用牛頓迭代法。當計算結果為負值時，塑性因子將取為零，相當于沒有發生塑性變形。應力不變量的更新值可由式（35）、（36）計算獲得，有效應力張量為

在上述計算完成后，還需采用硬化規律計算屈服面的更新位置，同時對硬化參數進行更新。

式（40）中Mp的計算要采用當前的孔隙比。

5 模型參數分析及力學響應

5.1 模型參數

模型參數總計10個如表1所示，即：3個彈性常數K0、μ（或G）和n；4個塑性參數ζp、D、m 和φcs（φcs也是臨界狀態參數）；3個臨界狀態參數eref、λ、ξ。

表1 模型參數表

除了臨界狀態參數（包括φcs），其余6個參數均可以通過各向同性壓縮和三軸剪切試驗獲得，限于篇幅，這里不再詳述參數確定程序。

5.2 模型力學響應

圖4是本構模型在不排水三軸應力條件下的力學響應，模型參數取值如表1，圖4（a）是不同初始孔隙比試樣在同一固結圍壓（200 k Pa）下的應力 應變曲線，圖4（b）是對應的應力路徑；圖4（c）、（d）是同一初始孔隙比試樣在不同固結圍壓下的應力 應變關系曲線和應力路徑。

從圖中可以看出，本文提出的本構模型能夠反映密實狀態（或初始孔隙比）對散粒體力學行為的影響，如圖4（a）、（b）所示：在同一固結圍壓下不同初始孔隙比導致了散粒體不同的剪脹、剪縮行為。不排水條件下，隨著剪應變的發展，對于初始孔隙比＝0.7、0.725的密實散粒體發生剪切硬化，而初始孔隙比＝0.75、0.8松散散粒體在達到峰值應力后產生了剪切軟化，隨著超孔隙水壓力的增長，有效應力降低，應力路徑向原點發展，發生了靜力液化。

模型還能考慮散粒體力學響應的圍壓依賴性，如圖4（c）、（d）所示，對初始孔隙比為0.8的散粒體在不同固結圍壓（200、400、800、1 200 kPa）下表現出不同的力學響應，低固結圍壓下散粒體更易于發生靜力液化。本構方程的數值結果顯示，本文提出的模型可以模擬散粒體如砂土等的不排水剪切力學特性。

6 模型的試驗驗證

為了進一步驗證模型，首先選Toyoura砂三軸不排水試驗結果進行比較，然后對砂 粉混合土的三軸不排水試驗結果進行模擬，驗證本文提出的模型應用于一般散粒體的可行性。

6.1 Toyoura砂

圖4 不同初始孔隙比和固結圍壓的模型響應

Verdugo等［20］對Toyoura砂進行了一系列三軸不排水剪切試驗，試驗固結圍壓為100、1 000、2 000、3 000 k Pa。本文對初始孔隙比為0.833的Toyoura砂在不同初始圍壓下的不排水響應進行模擬，圖5是本文模型的預測結果與試驗數據的對比，其中連續曲線為數值計算結果，模型參數見表2。

從圖5中可見，模型模擬結果和試驗結果基本吻合，雖然在應力－應變曲線峰值后的一小段區間內應力水平要略小于試驗值，以及應力路徑的中部稍有偏差，但從整體趨勢看，本文提出的模型較好地描述了Toyoura砂的不排水三軸力學特性。

表2 模型參數表

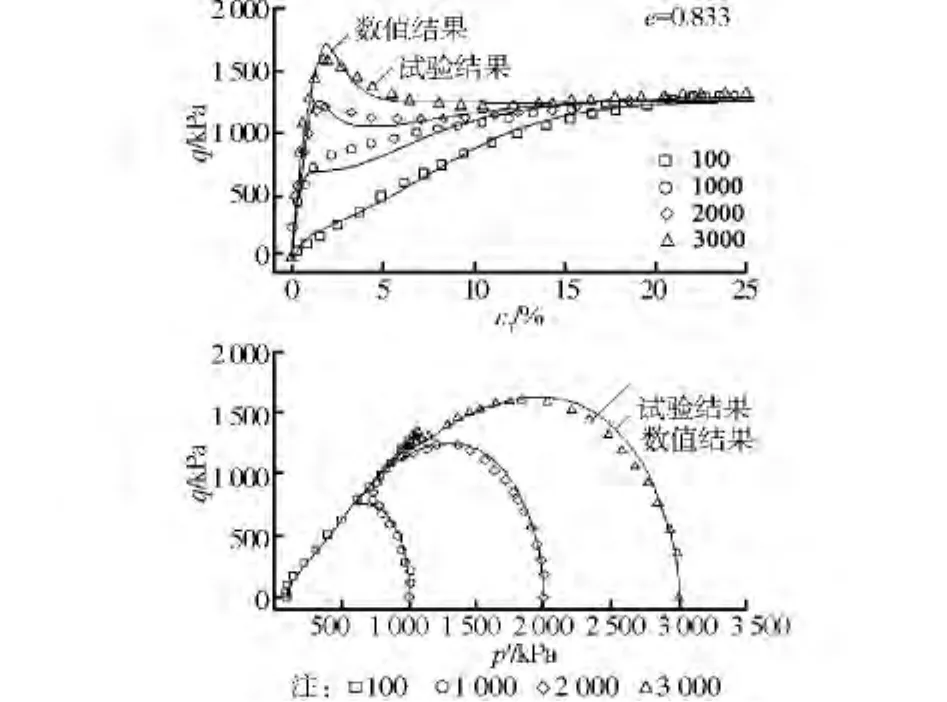
圖5 Toyoura砂試驗與模型模擬結果

6.2 砂 粉混合土

Yang［21］對Hokksund砂和中國黃河下三角洲埕北海區粉土混合土進行了一系列不排水三軸試驗。試驗在3個圍壓5、100、150 k Pa下進行，除了部分試樣在低圍壓很快液化，其余試驗壓縮至軸向應變20%左右達到穩態。限于篇幅，我們選取粉粒含量為5%、30%兩組試驗結果來評價本文提出模型的應用于砂 粉混合散粒體的可行性。模型參數如表2所示，圖6是應力 應變關系曲線和應力路徑的試驗數據和模型預測結果。

圖6 砂 粉混合土試驗與模型模擬結果

從圖中可以看出，對低粉粒含量（5%）的混合土，低圍壓下更容易產生液化，50、100 k Pa的模擬結果與試驗結果較吻合，150 k Pa的試驗點較離散，模擬結果稍差；對30%含量的混合土，全部圍壓下試樣均產生了完全的靜力液化，有效應力減少至零，模型模擬結果在峰值強度上稍低，但整體上與試驗結果吻合較好。

6.3 討 論

從對Toyoura砂和砂 粉混合土三軸不排水試驗的模擬結果看，本文提出的模型可以較好地應用于一般砂土和砂 粉混合散粒體。但需要指出的是，對于砂 粉混合散粒體，基于顆粒形狀、砂和粉粒顆粒粒徑和相對含量的多少，需要采用不同的模型參數進行預測，從表2中可以看出，對不同粉粒含量的混合土，模型參數雖有差別但比較接近，進一步工作應尋求砂 粉土混合物模型參數與粉粒含量之間的關系，期望能用統一的純砂和純粉土參數模擬砂 粉混合散粒體。

此外，本文模型的特點是在散粒體顆粒運動微觀力學分析的基礎上，模型的屈服函數和剪脹方程是通過積分粒間接觸本構方程和運動方程求得，這與一般彈塑性本構模型的建模思路不同。與Boukpeti等［18－19］提出的靜力液化本構關系比較，本文的模型參數較少且均具有明確的物理意義，可以通過室內常規三軸壓縮和剪切試驗結果獲取，方便應用。但與Dafalias等［22］提出的本構關系比較，本文的模型考慮了剪切硬化但沒有考慮旋轉硬化，因此在應用于各向異性砂土力學分析時尚有誤差，進一步的工作應考慮建立旋轉硬化或者引入組構參數使模型能夠應用于各向異性砂土的本構關系的模擬。

7 結 論

針對散粒體的靜力液化特性，基于散體微觀力學分析在臨界狀態土力學框架內建立了一個的靜力液化本構模型，研究初步得出了以下幾點結論：

1）提出的模型采用了臨界狀態理論，單調荷載下的排水和不排水應力路徑在臨界狀態處終止。模型硬化規律較合理，并采用了非關聯的流動法則，考慮了與材料狀態相關的剪脹性以及初始孔隙比、固結圍壓對散粒體應力－應變關系的影響。

2）本構模型的數值結果顯示，提出的模型可以較好地描述散粒體如砂土的不排水三軸剪切應力應變關系和應力路徑，模型參數簡單且物理意義較明確。

3）提出的模型與Toyoura砂和砂 粉混合土三軸不排水試驗的結果吻合較好，可以應用于散粒體的靜力液化問題分析。

［1］王剛，張建民.地震液化問題研究進展［J］.力學進展，2007，37（4）：575-589.

Wang G，Zhang J M.Recent advances in seismic liquefaction research ［J］.Advances in Mechanics，2007，37（4）：575-589.

［2］Desai C，Siriwardane H.Constitutive laws for engineering materials with emphasis on geologic materials ［M］.Printice-Hall，Eaglewood Cliff，NJ，1984.

［3］Prevost J.A simple plasticity theory for cohesioless soils［J］.Soil Dynamics and Earthquake Engineering，1985，4（1）：9-17.

［4］Dafalias Y，Herrmann L.Bounding surface formulation of soil plasticity ［C］／／Soil Mechanics-transient and Cyclic Loads，Wiley，1982，London：253-282.

［5］Chang C S，Misra A.Initial moduli of particulated mass with frictional contacts［J］.International Journal for Numerical and Analytcal Methods Geomech，1989，13（6）：629-644.

［6］Jenkins J T，Strack O D.Mean-field inelastic behavior of random arrays of identical spheres［J］.Mechanics of Material，1993，16：25-33.

［7］Chang C S，Hicher P Y.An elasto-plastic model for granular materials with microstructural consideration［J］.Intermational Journal of Solids ＆ Structures，2005，42：4258-4277.

［8］Yin Z Y， Chang C S， Hicher P Y，et al.Micromechanical analysis of kinematic hardening in natural clay ［J］.International Journal of Plasticity，2009，25（8）：1413-1435.

［9］Nicot F，Darve F.Basic features of plastic strains：From micro-mechanics to incrementally nonlinear models［J］.International Journal of Plasticity，2007，23：1555-1588.

［10］Nicot F S， Darve F.Failure in rate-independent granular materials as a bifurcation toward a dynamic regime［J］.International Journal of Plasticity，2012，29（1）：136-154.

［11］Misra A，Yang Y.Micromechanical model for cohesive materials based upon pseudo-granular structure ［J］.International Journal of Solids ＆Structures，2010，47：2970-2981.

［12］Lai Y Y，Li S.Strength criterion and elastoplastic constitutive model of frozen silt in generalized plastic mechanics ［J］.International Journal of Plasticity，2010，26（10）：1461-1484.

［13］Zhang W，Zhao C. Micromechanics analysis for unsaturated granular soils［J］.Acta Mechanica Solida Sinica，2011，24（3）：273-281.

［14］Tran T H， Bonnet G. A micromechanics-based approach for derivation of constitutive elastic coefficients of strain-gradient media ［J］.International Journal of Solids ＆Structures，2012，49（5）：783-792.

［15］Shen W Q，Gatmiri B.A micro-macro model for clayey rocks with a plastic compressible porous matrix ［J］.International Journal of Plasticity，2012，36：64-85.

［16］Mro′z Z，Nboukpeti N，Drescher A.Constitutive model for static liquefaction［J］.International Journal of Geomechanics，2003，3（2）：133-144.

［17］Boukpeti N，Drescher A.Triaxial behavior of refined Superior sand model［J］.Computers and Geotechnics，2000，26：65-81.

［18］Castro G，Poulos S，France J，et al.Liquefaction induced by cyclic loading ［R］.National Science Foundation，1982.

［19］Casagrande A.Liquefaction and cyclic mobility of sands，a critical review［D］.Harvard University，1976.

［20］Verdugo R，Ishihara K.The steady state of sandy soils［J］.Soils and Foundations，1996，36（2）：81-91.

［21］Yang L S.Characterization of the properties of sand-silt mixtures ［D］. Norwegian Univ. Sci. Tech.，Trondheim，Norway，2004.

［22］Dafaliasy F，Manzari T M.Simple plasticity sand model accounting for fabric change effects［J］.Journal of Engineering Mechanics，2004，130（6）：622-634.

（編輯 王秀玲）

A Static Liquefaction Constitutive Model for Granular Materials Based on the Micromechanical Analysis

Liu Yang1，Wang Chenglin1，Yan Hongxiang2
（1.Department of Civil Engineering，University of Science and Technology Beijing，Beijing 100083，P.R.China；2.China Highway Engineering Consulting Corporation，Beijing 100097，P.R.China）

Based on the static liquefaction of granular materials，an elastoplastic static liquefaction constitutive model was proposed in the framework of critical state soil mechanics.The yielding surface and hardening rules were obtained by integrating the contact force of the model proposed by Chang and a nonassociate flow rule was adopted as well.The model has taken the state dependent dialatency law and the effect of initial density to the stress-strain relationship into consideration.The parameters of the model are simple and have certain physical meanings.The predicted results obtained by the model have a good agreement with the undrained triaxial test of Toyoura sand and sand-silt mixture.

granular material；static liquefaction；constitutive model；numerical simulation

TU443

A

1674-4764（2014）03-0011-07

10.11835／j.issn.1674-4764.2014.03.003

2013-09-10

國家自然科學基金（51178044）；新世紀優秀人才資助項目（NCET-11-0579）；中央高校基本科研業務費（FRFTP-12-001B）；北京高校“青年英才計劃”

劉洋（1979-），男，博士，副教授，主要從事巖土工程研究，（E-mail）imaginationly＠163.com。