高強混凝土剪力墻屈服位移計算方法

趙花靜，梁興文，宋 璨

（西安建筑科技大學a.理學院；b.土木工程學院，西安 710055）

高強混凝土剪力墻屈服位移計算方法

趙花靜，梁興文，宋 璨

（西安建筑科技大學a.理學院；b.土木工程學院，西安 710055）

考慮高強混凝土受壓強度高等特點，在高強混凝土剪力墻截面剛達到屈服狀態時，假定截面受壓區混凝土壓應力為線性分布，基于平截面假定，用彎矩 曲率分析法得到了剪力墻截面屈服曲率公式。采用屈服曲率公式，對影響高強混凝土剪力墻屈服曲率的參數進行了分析。結果表明，除軸壓比外，縱向受力鋼筋屈服應變對屈服曲率影響最大；在軸壓比較大時，剪力墻截面兩端翼墻的影響也較大。通過對計算結果的回歸分析，提出了考慮軸壓比、縱向受力鋼筋屈服應變和剪力墻截面兩端翼墻面積影響的屈服曲率計算公式。提出了高強混凝土剪力墻頂點屈服位移的計算公式，公式的計算值與12個高強混凝土高懸臂墻頂點屈服位移的試驗值比較吻合。簡化公式也適用于普通混凝土剪力墻的屈服位移計算。

高強混凝土；剪力墻；屈服曲率；屈服位移；抗震性能設計

20世紀90年代以來，建筑結構基于變形／位移的抗震設計受到地震工程界的廣泛關注，并提出了一些具體的設計理論和方法［1－9］。其中有些方法在設計開始即以結構變形（側移等）作為設計變量，選取性能準則，確定滿足性能準則的基底剪力需求，然后對結構進行剛度和承載力設計，并對構件截面進行變形能力設計。Tjhin等［8］采用剪力墻頂點屈服側移和墻基礎處的塑性轉角作為設計變量，對剪力墻結構進行設計。結果表明，剪力墻頂點屈服側移和墻基礎處的塑性轉角均有可能控制設計，取決于所采用的性能目標。

用基于位移的抗震設計方法對剪力墻結構進行設計時，其屈服位移是一個重要參數。Wallace等［1］認為普通混凝土剪力墻的屈服曲率范圍在0.002 5／hw和0.003 5／hw之間或以上，其中hw是剪力墻截面高度。Priestley等［2］為了簡化計算，提出的剪力墻截面屈服曲率計算公式僅與縱向受力鋼筋的屈服應變和截面高度有關。錢稼茹等［3］基于平截面假定給出了混凝土剪力墻截面屈服曲率的計算公式，并根據試驗結果，提出了剪力墻截面屈服時受壓邊緣混凝土應變的計算公式。Tjhin等［5］采用彎矩 曲率分析法，給出了延性混凝土剪力墻屈服位移的計算公式，其屈服位移公式僅與軸壓比和縱向受力鋼筋的屈服應變有關。上述關于混凝土剪力墻屈服曲率或屈服位移的計算方法或公式，基本上是以普通混凝土剪力墻為研究對象而提出的，由于高強混凝土的脆性以及一些基本性能參數與普通混凝土有一定差異，因此本文以高強混凝土剪力墻作為研究對象提出其頂點屈服位移的計算公式。

高強混凝土具有高強度、高耐久性、高流動性及高抗滲性能等優點，在高層及超高層建筑的底部若干層采用高強混凝土剪力墻抵抗水平荷載，可以減小剪力墻厚度，提高房屋的使用面積，具有明顯的經濟效益和社會效益。因此，研究高強混凝土剪力墻屈服位移的計算方法，將為這種剪力墻結構基于位移的抗震設計提供依據。

考慮高強混凝土受壓強度高等特點，假定截面屈服時受壓區混凝土壓應力為線性分布，基于平截面假定，用彎矩 曲率分析法得到了剪力墻截面屈服曲率公式。采用參數分析法，對影響高強混凝土剪力墻屈服曲率的參數進行了分析，提出了考慮軸壓比、縱向受力鋼筋屈服應變和剪力墻截面兩端翼墻面積影響的屈服曲率簡化計算公式以及相應的剪力墻頂點屈服位移計算公式。

1 剪力墻截面屈服曲率計算

1.1 骨架曲線

根據剪力墻試件在低周反復水平荷載作用下的滯回曲線，取其外包線得骨架曲線，并將其簡化為4線型，如 圖 1 所 示。圖 中 Mcr、φcr、My、φy、Mp、φp、Mu、φu分別表示開裂點、屈服點、峰值點和極限點對應的彎矩和曲率。

圖1 彎矩 曲率骨架曲線

1.2 剪力墻截面屈服時的應力、應變分布

對于高懸臂混凝土剪力墻，以彎曲變形為主，故假定截面在變形后保持平面。當混凝土剪力墻截面受拉區縱向受力鋼筋應變達到鋼筋屈服應變εy時，剪力墻截面達到屈服極限狀態，相應的受壓區邊緣混凝土應變為εc，如圖2（a）所示。分析時不考慮受拉混凝土的作用；由于高強混凝土的受壓強度很高，故假定受壓區混凝土應力仍為線性分布，如圖2（b）所示。在平截面假定的前提下，對稱配筋矩形截面剪力墻在屈服狀態下的截面豎向分布鋼筋的應力分布如圖2（c）所示。

圖2 剪力墻截面屈服狀態應力、應變圖

1.3 平衡方程

由圖2（a）所示的剪力墻截面應變分布，可得截面的屈服曲率φy為式中：εy為鋼筋的屈服應變；hw0為剪力墻截面有效高度；ξ為剪力墻截面受壓區相對計算高度。

屈服曲率φy可采用彎矩 曲率分析來確定，應滿足應變協調、材料應力 應變關系和平衡條件。

根據圖2所示的截面豎向力的平衡條件，可得

式中：bw為剪力墻截面厚度；hw、hw0分別為剪力墻的截面高度、有效高度；ρs、ρ′s分別為截面端部受拉、受壓縱筋的配筋率；ρw為腹板豎向分布鋼筋配筋率；fc為混凝土軸心抗壓強度；fy為受拉鋼筋的屈服強度；Es、Ec分別為鋼筋和混凝土的彈性模量；λn為軸壓比；a′s為受壓鋼筋合力點至截面受壓區邊緣的距離；As、A′s分別為受拉和受壓區縱向鋼筋的截面面積。

聯立公式（1）與（2），可求得截面相對受壓區高度ξ和屈服曲率φy。

1.4 影響因素分析

由式（2）可見，影響混凝土剪力墻截面屈服曲率的因素有：截面尺寸bw和hw、截面受壓區相對高度ξ、截面端部受拉、受壓鋼筋的配筋率ρs、ρ′s、腹板豎向分布鋼筋配筋率ρw、混凝土軸心抗壓強度fc、鋼筋屈服強度fy和軸壓比λn等。為了分析各因素對截面屈服曲率的影響程度，表1列出了各因素的變化范圍及取值；對于I形截面剪力墻，還考慮了翼墻尺寸的影響。

表1 參數及取值

對表1所列的5個參數（有翼墻時為6個參數），每次考察其中一個參數，其他參數取固定值（取其常用值），對所考察的參數，分別按表1取值，計算其屈服曲率，并繪出屈服曲率與相應參數的關系曲線，考察其變化規律及相關性。分析步驟如下：

1）選定截面尺寸、材料強度，確定所考察的參數及其他參數，聯立求解方程（1）與（2），得到屈服曲率。

2）變化所選定的參數，重復第（1）步，得到相應的屈服曲率。

3）繪出屈服曲率與相應參數的關系曲線。

4）評價其相關性。

按上述方法，共進行了40組（有翼墻時為160組）分析，繪制了40組（有翼墻時為160組）屈服曲率與相應參數的關系曲線，各組曲線規律基本相同。圖3為其中的一組，繪制這組曲線所采用的參數為：截面尺寸為250 mm×6 000 mm，端部縱筋配筋率取0.5%，腹板豎向分布鋼筋配筋率取0.30%，混凝土強度等級取C60，端部受力鋼筋取HRB400，豎向分布鋼筋取HRB335，混凝土和鋼筋強度分別取其平均值，軸壓比取0.20，工字型截面端部縱筋配筋率取2%，翼墻長寬比取5.0。

圖3中的每個圖均以軸壓比λn為橫坐標，以屈服曲率系數kφ（屈服曲率與截面有效高度hw0之乘積）為縱坐標，繪制當端部縱筋配筋率ρs、腹板豎向分布鋼筋配筋率ρw、混凝土強度fc以及鋼筋屈服強度fy分別取不同值時與曲率的關系圖。

從圖3可以看出，對于所考慮參數的取值范圍，矩型截面和I型截面的屈服曲率與相應參數的關系曲線都表現出相同的規律。由圖3（a）、（b）可見，腹板豎向分布鋼筋配筋率對矩形截面屈服曲率幾乎沒有影響，對工字型截面，當軸壓比較大時，腹板豎向分布鋼筋配筋率對屈服曲率影響越來越小。由圖3（c）、（d）可見，軸壓比較大時，混凝土強度對屈服曲率產生一定影響，但在軸壓比為0.3時，影響程度只有8.6%（（4.4－4.05）／4.05＝8.6%）。由圖3（e）、（f）可見，端部縱筋配筋率隨著軸壓比的增大，其影響程度越來越小，當軸壓比為0.3時，影響程度只有7%。由圖3（g）、（h）、（i）可見，鋼筋強度等級對屈服曲率影響最大，剪力墻兩端的翼墻尺寸對屈服曲率的影響較大。

圖3 不同參數時屈服曲率系數

1.4 剪力墻截面屈服曲率的簡化計算公式

由上述分析可見，對屈服曲率影響較大的因素除軸壓比外，還有縱向受力鋼筋的應變和剪力墻兩端翼墻面積。另外，由圖3可見，屈服曲率與軸壓比、縱向受力鋼筋的應變和剪力墻兩端翼墻面積均近似呈線性關系，故可用線性函數關系進行分析。

經過多元線性回歸分析，得出屈服曲率的方程為

式（3）適用于矩形截面剪力墻；式（4）適用于工字型截面剪力墻，其中ω表示剪力墻截面一端兩側翼墻面積之和與全截面面積之比值。

2 屈服位移計算

定義剪力墻基礎頂面截面彎曲屈服時相應的位移為屈服位移，且僅考慮截面彎曲變形的影響。當假定剪力墻的質量和剛度沿高度分布均勻時，對作用頂點集中荷載、均布荷載和倒三角形分布荷載的剪力墻，其頂點屈服位移分別為

式中，αΔ為剪力墻頂點屈服位移系數，其值主要取決于荷載形式。

實際工程中的剪力墻比較復雜，其質量和剛度沿高度有變化，各質點處的水平地震作用一般與其質量和側移值有關，頂點屈服位移亦如此。因此，確定剪力墻頂點屈服位移系數αΔ時，可采用第一振型的振型值與質量乘積成比例的側向力分布，并考慮剪力墻截面開裂對其剛度的影響，按彈性分析方法計算，其結果見表2，其中n表示剪力墻結構的總層數。

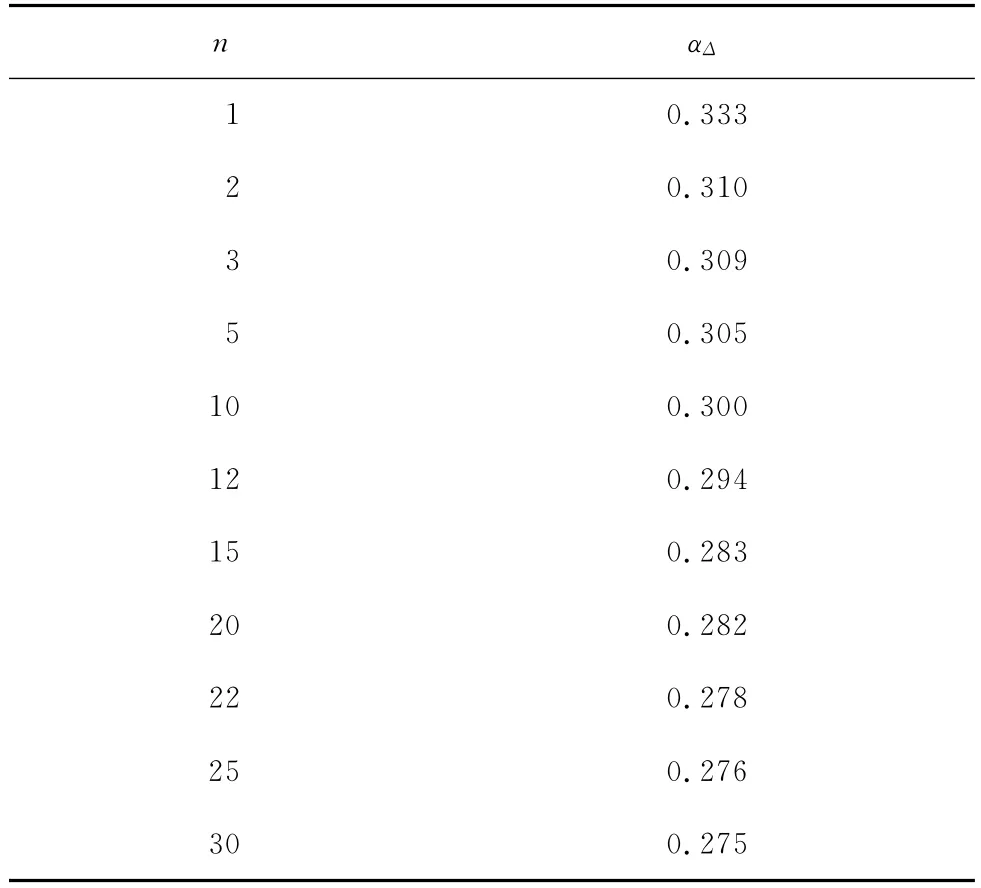
表2 剪力墻頂點屈服位移系數αΔ

3 試驗驗證

3.1 試驗數據

試驗數據取自文獻［11～14］，實測混凝土立方體抗壓強度在72.97～93.85 N／mm2之間，計算時混凝土強度取其軸心抗壓強度平均值，鋼筋強度取屈服強度平均值。12個懸臂高強混凝土剪力墻試件參數如表3所示，其中HPCW-1～HPCW-4為矩形截面高性能混凝土剪力墻，SHSCW-1～SHPCW-8均為矩形截面的型鋼高強混凝土剪力墻。所有試件均在剪力墻頂點作用水平集中荷載，且均發生彎曲破壞。

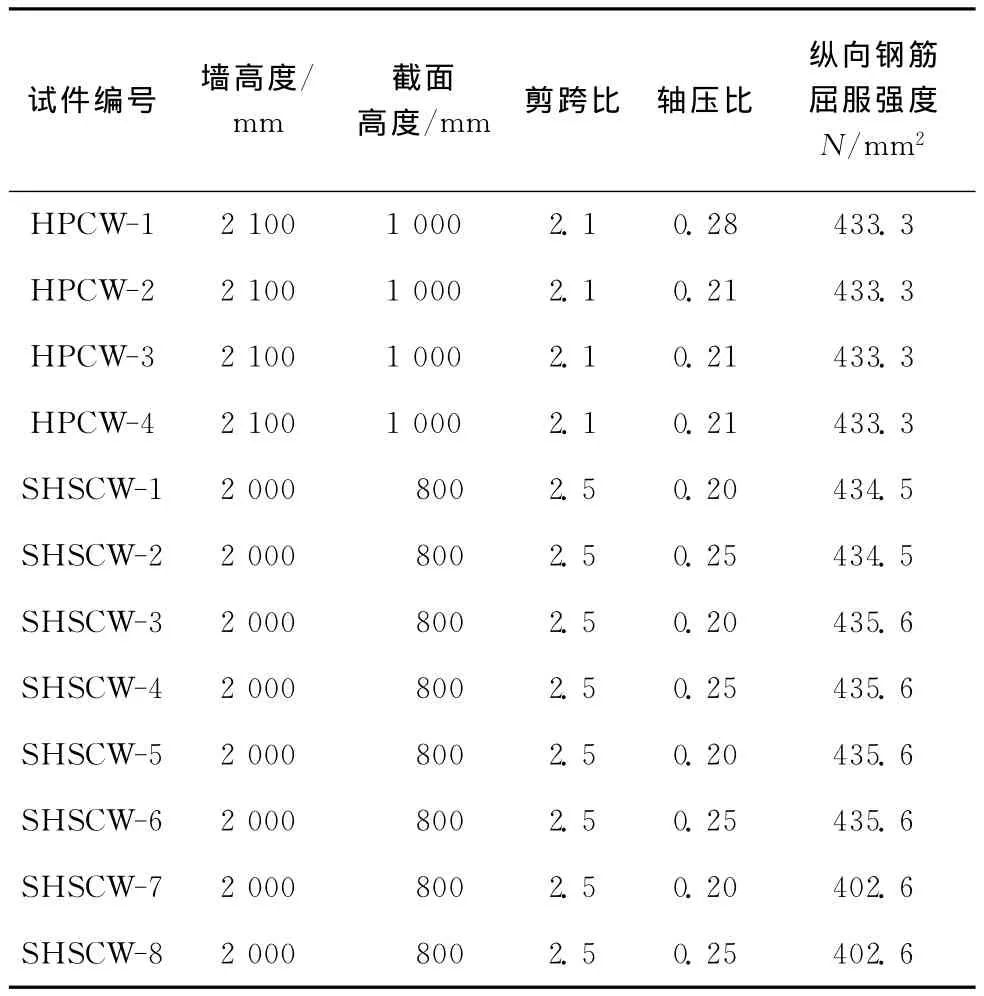
表3 試件參數

3.2 屈服位移計算值與試驗值的比較

按式（3）計算剪力墻基礎頂面截面的屈服曲率，按式（7）計算剪力墻頂點屈服位移，其中屈服位移系數αΔ取1／3，同時考慮剪力墻開裂后剛度的退化，其計算結果如表4所示。從表4可見，按本文公式計算所得的屈服位移值與試驗值相比，誤差在10%以內，吻合較好。

表4 屈服位移計算值與試驗值的比較

4 結 論

1）彎矩 曲率分析結果表明，影響高強混凝土剪力墻屈服曲率的因素有：截面端部受拉、受壓鋼筋的配筋率、腹板豎向分布鋼筋配筋率、混凝土軸心抗壓強度、鋼筋屈服強度和軸壓比。在這些因素中，對剪力墻截面屈服曲率影響最大的因素為縱向受力鋼筋的屈服應變，其次為軸壓比；在軸壓比較大時，剪力墻截面兩端的翼墻也有一定影響。

2）本文提出的高強混凝土剪力墻截面屈服曲率計算公式，考慮了軸壓比、縱向受力鋼筋屈服應變和剪力墻截面兩端翼墻的影響。基于該屈服曲率公式，所得的剪力墻頂點屈服位移計算公式，其計算值與12個高懸臂高強混凝土剪力墻屈服位移試驗值比較吻合。因混凝土對其影響不大，該屈服位移計算公式也適用于普通混凝土剪力墻的屈服位移計算。

［1］Wallace J W，Moehle J P.Ductility and detailing requirements of bearing wall buildings［J］.Journal of Structural Engineering，1992，118（6）：1625-1644

［2］Priestley M J N.Aspect of drift and ductility capacity of rectangular cantilever structural walls［J］.Bulletin of New Zealand Society for Earthquake Engineering，1998，31（2）：73-85.

［3］錢稼茹，呂文，方鄂華.基于位移延性的剪力墻抗震設計［J］.建筑結構學報，1999，20（3）：42-49.

Qian J R，Lyu W，Fang E H.Displacement ductilitybased aseismic design for shear walls［J］.Journal of Building Structures，1999，20（3）：42-49.

［4］Thomsen J H，Wallace J.Displacement-based design of slender reinforced concrete walls-experimental verification ［J］.Journal of Structural Engineering，2004，130（4）：618-630.

［5］Tjen N T，Mark A A，John W W.Yield displacement estimates for displacement-based seismic design of ductile reinforced concrete structural wall buildings ［C］／／13thWorld Conference on Earthquake Engineering，Vancouver B C，Canada 2004.

［6］梁興文，黃雅捷，楊其偉.鋼筋混凝土框架結構基于位移的抗震設計方法研究［J］.土木工程學報，2005，38（9）：53-60.

Liang X W，Huang Y J，Yang Q W.Displacementbased seismic design method of RC frames［J］.China Civil Engineering Journal，2005，38（9）：53-60.

［7］錢稼茹，徐福江.鋼筋混凝土剪力墻基于位移的變形能力設計方法［J］.清華大學學報：自然科學版，2007，47（3）：305-308.

Qian J R，Xu F J.Displacement-based deformation capacity design method of RC cantilever walls［J］.Journal of Tsinghua University：Science and Technology，2007，47（3）：305-308.

［8］Tjen N，Tjhin M A，Aschheim J W W.Yield displacement-based seismic design of RC wall buildings［J］.Engineering Structures，2007，29：2946-2959.

［9］梁興文，趙花靜，鄧明科.考慮邊緣約束構件影響的高強混凝土剪力墻彎矩 曲率骨架曲線參數研究［J］.建筑結構學報，2009（Sup 2）：62-67.

Liang X W，Zhao H J，Deng M K.Moment–curvature relationship analysis of high-strength concrete shear wall with partially confined end-zones ［J］.Journal of Building Structures，2009（Sup 2）：62-67.

［10］應勇.鋼筋混凝土剪力墻構件屈服位移研究［J］.低溫建筑技術，2010，12：38-40.

Ying Y.Study on yield displacement for reinforced concrete shear walls ［J］. Low Temperature Architecture Technology，2010，12：38-40.

［11］梁興文，鄧明科，張興虎，等.高性能混凝土剪力墻性能設計理論的試驗研究［J］.建筑結構學報，2007，28（5）：80-88.

Liang X W，Deng M K，Zhang X H，et al.Experimental study on performance-based seismic design of high performance concrete shear wall ［J］.Journal of Structural Engineering，2007，28（5）：80-88.

［12］梁興文，辛力，鄧明科，等.高性能混凝土剪力墻抗震性能及其性能指標試驗研究［J］.土木工程學報，2010，43（11）：55-59.

Liang X W，Xin L，Deng M K，et al.Experimental study on seismic behavior and performance indexes of high-strength concrete shear walls ［J］.China Civil Engineering Journal，2010，43（11）.

［13］梁興文，楊鵬輝，崔曉玲，等.帶端柱高強混凝土剪力墻抗震性能試驗研究［J］.建筑結構學報，2010，31（1）：23-32.

Liang X W，Yang P H，Cui X L，et al.Experimental study on seismic behavior of high performance concrete shear wall with boundary columns ［J］.Journal of Building Structures，2010，31（1）：23-32.

［14］梁興文，馬愷澤，李菲菲，等.型鋼高強混凝土剪力墻抗震性能試驗研究［J］.建筑結構學報，2011，32（6）：68-75.

Liang X W，Ma K Z，Li F F，et al.Experimental study on seismic behavior of SHSC structural walls ［J］.Journal of Building Structures，2011，32（6）：68-75.

［15］梁興文，寇佳亮，鄧明科.高強混凝土剪力墻性能指標研究［J］.建筑結構，2012，42（4）：90-93.

Liang X W，Kou J L，Deng M K.Reseach on performance index of high-strength concrete shear walls［J］.Building Structure，2012，42（4）：90-93.

（編輯 胡 玲）

Yield Displacement Calculation Method of High-Strength Concrete Shear Wall

Zhao Huajing，Liang Xingwen，Song Can

（a.College of Science；b.School of Civil Engineering，Xi＇an University of Architecture and Technology，Xi＇an 710055，P.R.China）

It is assumed that concrete compressive stress of the cross-section compression zone is linear distribution when the cross-section of high-strength concrete shear wall reaches yield situation.Based on the plane section assumption，the yield curvature formula of shear wall section is obtained by using moment-curvature analysis method.The parameters affecting yield curvature of high-strength concrete shear wall are studied by using the yield curvature formula.The results show that longitudinal reinforcement yield strain is the most vital factor of the yield curvature in addition to axial load ratio.When axial load ratio is larger，both wing walls of shear wall section have larger impact.The yield curvature formula is presented，considering the impact of axial load ratio，boundary reinforcement yield stress and both ends of wing walls of shear wall section based on the regression analysis of calculation results.On this basis，the vertex yield displacement formula of high-strength concrete shear wall is proposed，and the calculation results of formula correspond well to the vertex yield displacement experimental values of the 12 high-strength concrete cantilever wall.The formula is also suited for the vertex yield displacement of comment concrete shear wall.

high-strength concrete；shear wall；yield curvature；yield displacement；performance-based seismic design

TU 356.1

A

1674-4764（2014）03-0080-06

10.11835／j.issn.1674-4764.2014.03.013

2013-12-17

國家自然科學基金（81278402、51078305、50908187）；長江學者和創新團隊發展計劃（PCSIRT）。

趙花靜（1985-），女，主要從事高層建筑結構及其抗震性能設計理論研究，（E-mail）zhaohj0602＠126.com。