魯棒Kalman濾波陀螺隨機(jī)噪聲AR快速/實(shí)時(shí)建模
黃 磊,趙亞琴
(南京林業(yè)大學(xué)機(jī)電學(xué)院自動(dòng)化系,江蘇 南京 210037)
魯棒Kalman濾波陀螺隨機(jī)噪聲AR快速/實(shí)時(shí)建模
黃 磊,趙亞琴
(南京林業(yè)大學(xué)機(jī)電學(xué)院自動(dòng)化系,江蘇 南京 210037)
針對(duì)傳統(tǒng)陀螺隨機(jī)噪聲的AR建模方法收斂速度慢、所需樣本多等問(wèn)題,提出新的基于魯棒Kalman濾波的陀螺隨機(jī)噪聲AR建模方法。該方法將AR模型參數(shù)作為系統(tǒng)的狀態(tài)量,采用未知時(shí)變的噪聲統(tǒng)計(jì)估值器估計(jì)觀測(cè)噪聲的均值和方差,通過(guò)Kalman濾波估計(jì)出AR模型參數(shù)。實(shí)驗(yàn)結(jié)果表明:這種AR建模方法具有收斂速度快,時(shí)間開銷少的優(yōu)點(diǎn)。當(dāng)有新的噪聲數(shù)據(jù)到來(lái)時(shí),還能使建立的AR模型得到及時(shí)更新,提高建模準(zhǔn)確度,適用于快速建模或陀螺隨機(jī)噪聲具有強(qiáng)時(shí)變性的工程場(chǎng)合。
捷聯(lián)慣性導(dǎo)航系統(tǒng);陀螺隨機(jī)噪聲建模;魯棒Kalman濾波器;時(shí)間序列
0 引 言
在捷聯(lián)慣導(dǎo)和組合導(dǎo)航系統(tǒng)中,經(jīng)常要對(duì)陀螺儀的誤差建模,通過(guò)補(bǔ)償手段提高陀螺儀的使用精度[1-3]。陀螺儀的輸出誤差由確定性誤差(如零偏、刻度因數(shù)誤差等)和隨機(jī)誤差構(gòu)成。確定性誤差一般可以通過(guò)實(shí)驗(yàn)標(biāo)定的方法加以補(bǔ)償。隨機(jī)誤差只能從信號(hào)處理的角度,建立誤差的數(shù)學(xué)模型,繼而采用濾波等手段消除。在這個(gè)過(guò)程中基于時(shí)間序列建模的方法得到了廣泛應(yīng)用。
當(dāng)前對(duì)陀螺儀隨機(jī)噪聲的時(shí)間序列建模很多是基于AR(自回歸)模型進(jìn)行的[4-5]。傳統(tǒng)的AR建模方法有最小二乘法、Yule-Walker方程估計(jì)法等,但這些傳統(tǒng)的建模方法所需樣本數(shù)據(jù)較多,且不能及時(shí)反映陀螺隨機(jī)噪聲的時(shí)變特性。為解決這一問(wèn)題,本文提出了基于魯棒卡爾曼濾波的陀螺隨機(jī)噪聲AR建模方法。
1 陀螺隨機(jī)噪聲的平穩(wěn)隨機(jī)性檢驗(yàn)和定階
對(duì)某國(guó)產(chǎn)MEMS(微電子機(jī)械)陀螺進(jìn)行地面靜態(tài)實(shí)驗(yàn),所獲得的噪聲數(shù)據(jù)如圖1所示(共50000點(diǎn))。數(shù)據(jù)采樣率為14Hz,單位:deg/s。經(jīng)檢驗(yàn)該數(shù)據(jù)含有一定的常值項(xiàng)(由地球自轉(zhuǎn)角速度和陀螺的零偏等引起)。經(jīng)一階差分去除常值趨勢(shì)項(xiàng)后,得到滿足平穩(wěn)隨機(jī)性要求的隨機(jī)噪聲數(shù)據(jù)。分析該噪聲的自相關(guān)和偏相關(guān)特性,發(fā)現(xiàn)自相關(guān)系數(shù)呈現(xiàn)出拖尾性,而偏相關(guān)系數(shù)在k=2后截?cái)啵ㄈ鐖D2所示)。
根據(jù)時(shí)間序列分析理論,對(duì)于自相關(guān)函數(shù)呈現(xiàn)拖尾性而偏自相關(guān)函數(shù)呈現(xiàn)截尾性的平穩(wěn)隨機(jī)序列最適宜采用AR模型建模,且偏相關(guān)函數(shù)的截?cái)嗵幘褪悄P偷碾A數(shù)[6-8]。因此選擇2階AR模型建模最合適。
根據(jù)定義,AR(2)模型的數(shù)學(xué)描述為

式中ε(k)為均值為0方差未知的白噪聲。
2 基于魯棒Kalman濾波的AR模型建模方法
從式(1)可以看出,AR(2)模型的關(guān)鍵是根據(jù)觀測(cè)量z(k)求出各回歸項(xiàng)z(k-1)、z(k-2)的系數(shù)a1、a2。如果將a1、a2作為系統(tǒng)狀態(tài)量,通過(guò)建立合理的狀態(tài)方程和觀測(cè)方程,就可使用Kalman濾波器得到a1、a2的準(zhǔn)確估計(jì)。

圖1 某國(guó)產(chǎn)MEMS陀螺的噪聲數(shù)據(jù)
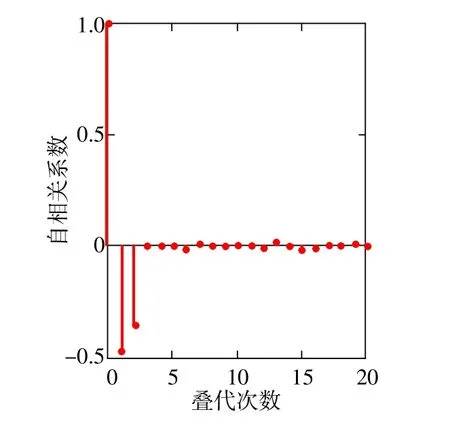
圖2 陀螺隨機(jī)噪聲的偏相關(guān)函數(shù)
2.1 系統(tǒng)方程
將AR(2)模型系數(shù)a1、a2定義為系統(tǒng)的狀態(tài)量:

則可把式(1)作為觀測(cè)方程:
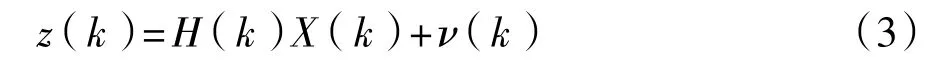
式中:H(k)=[z(k-1),z(k-2)],ν(k)=ε(k)。
考慮到當(dāng)陀螺儀的隨機(jī)噪聲特性穩(wěn)定時(shí),滿足一定的樣本數(shù)后,所建立的AR模型的參數(shù)應(yīng)穩(wěn)定收斂于真值,不再隨樣本數(shù)量的增加而增加。即1
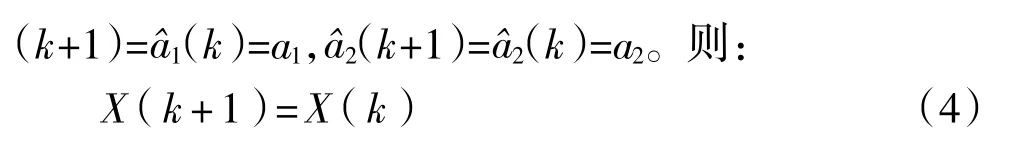
把式(4)作為狀態(tài)轉(zhuǎn)移方程。則系統(tǒng)狀態(tài)空間模型為

從式(5)可以看出,系統(tǒng)噪聲w(k)為0,狀態(tài)轉(zhuǎn)移陣Φ=I。則有:
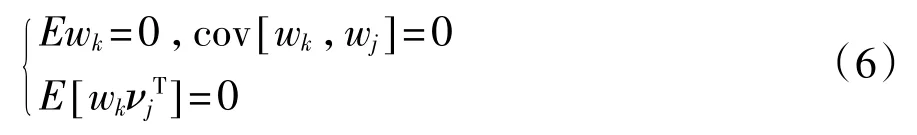
2.2 未知觀測(cè)噪聲的統(tǒng)計(jì)估值器
系統(tǒng)的觀測(cè)噪聲ν(k)主要由AR模型中的白噪聲ε(k)引起。由于ε(k)的方差特性未知,所以觀測(cè)噪聲ν(k)屬于統(tǒng)計(jì)特性未知的白噪聲。在魯邦Kalman濾波器中,通常采用帶遺忘因子的噪聲統(tǒng)計(jì)估值器估計(jì)未知噪聲特性[6]。該方法在估計(jì)觀測(cè)噪聲時(shí)強(qiáng)調(diào)新數(shù)據(jù)的作用,對(duì)于時(shí)間上過(guò)于古老的數(shù)據(jù)則漸漸遺忘。即采用漸消的記憶指數(shù)加權(quán)方法實(shí)現(xiàn)對(duì)未知噪聲的統(tǒng)計(jì)特性估計(jì)[6]:
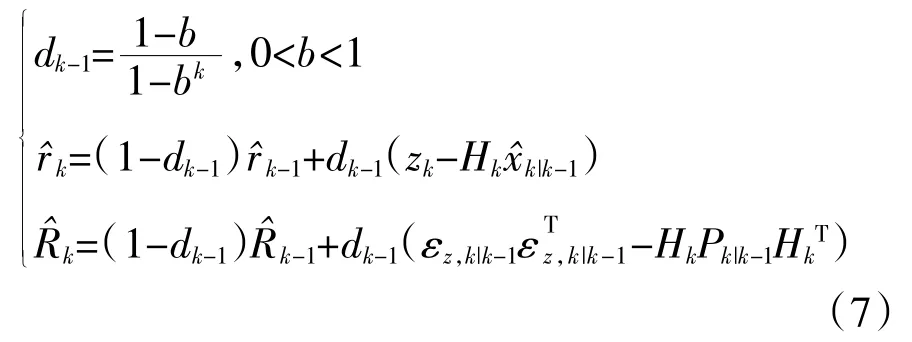
式中b稱為遺忘因子,一般取0.95<b<1。由Kalman濾波中的新息計(jì)算。
2.3 基于魯棒Kalman濾波的AR模型快速建模
式(5)給出了系統(tǒng)的狀態(tài)方程和觀測(cè)方程,式(6)、式(7)給出了系統(tǒng)噪聲和觀測(cè)噪聲的統(tǒng)計(jì)特性,該特性滿足卡爾曼濾波器的要求。因此可以應(yīng)用魯棒卡爾曼濾波器對(duì)狀態(tài)量,即AR(2)模型的2個(gè)參數(shù)進(jìn)行估計(jì)。魯棒卡爾曼濾波過(guò)程如下:
狀態(tài)一步預(yù)測(cè):

由于系統(tǒng)噪聲為0,狀態(tài)轉(zhuǎn)移陣Φ=I。因此一步預(yù)測(cè)誤差方差陣為
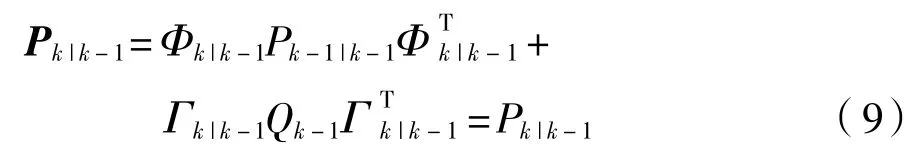
濾波增益矩陣為

新息為
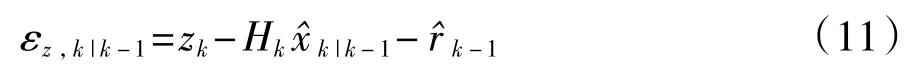
狀態(tài)估計(jì)為
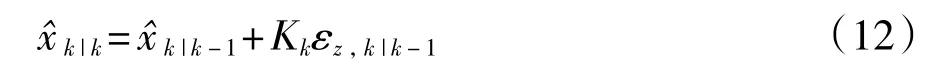
估計(jì)誤差方差陣為

圖3中的虛直線是Y-W法對(duì)1 h采樣數(shù)據(jù)的AR(2)模型建模結(jié)果:
采用新的基于魯棒Kalman濾波的AR模型參數(shù)估計(jì)結(jié)果如圖3中實(shí)曲線所示。在實(shí)際運(yùn)行時(shí),可以根據(jù)系統(tǒng)的建模精度要求設(shè)定閾值θ。如連續(xù)10次的運(yùn)行迭代結(jié)果中,狀態(tài)量估計(jì)值(也即1、2)的最大值和最小值之間的差異都小于該閾值θ,則認(rèn)為狀態(tài)估值已穩(wěn)定收斂。考慮到一般AR模型的參數(shù)估計(jì)精確到小數(shù)點(diǎn)后3位已足夠,這里選取θa1=θa2=0.001,則濾波器在運(yùn)行2150次后滿足條件退出,狀態(tài)量估計(jì)收斂于:
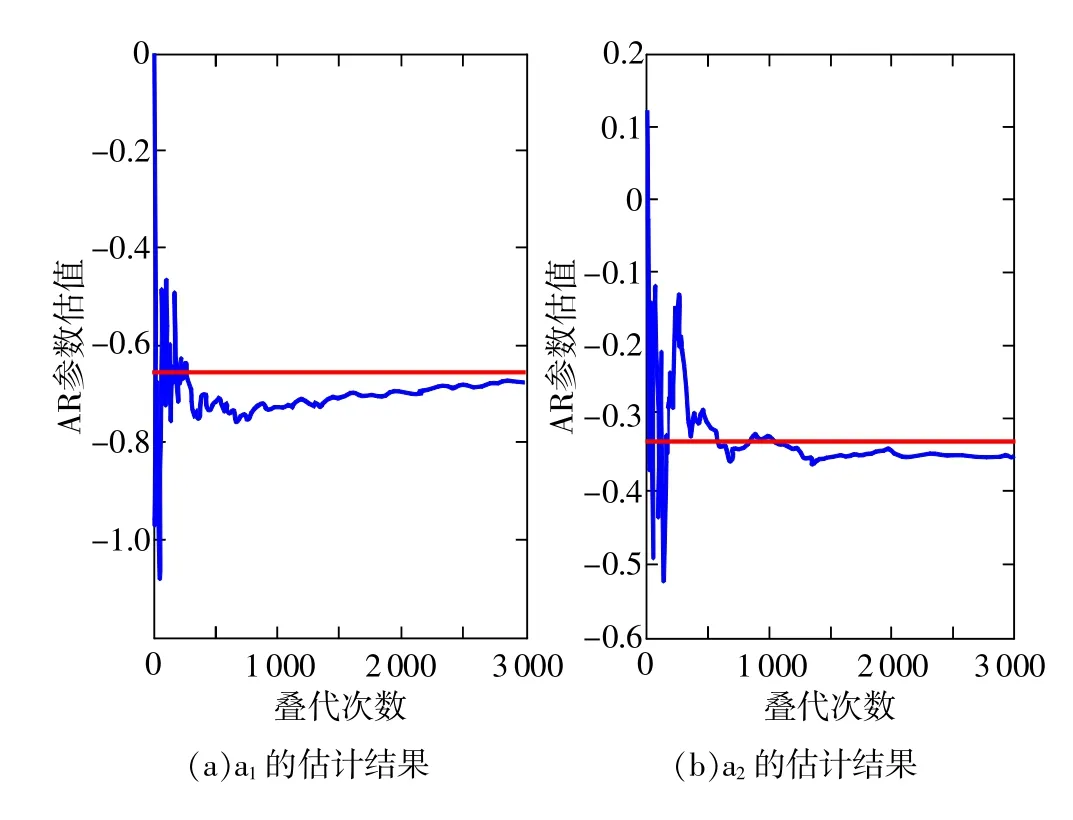
圖3 基于魯棒Kalman的AR(2)建模結(jié)果

式(15)即是采用魯棒卡爾曼濾波快速建模的結(jié)果,該過(guò)程僅需2150個(gè)樣本。式(14)是采用傳統(tǒng)Y-W對(duì)1 h樣本數(shù)據(jù)的建模結(jié)果。對(duì)比兩式可以看出,兩者的建模結(jié)果非常接近,相對(duì)差異為δα1=4.9%,δα2=6.2%。由于在有限樣本條件下,不同時(shí)間序列建模方法(如最小二乘法和Y-W法)的建模結(jié)果本就不會(huì)完全相同。這一波動(dòng)在大多數(shù)工程允許的精度范圍之內(nèi)(<10%)[6]。但新的建模方法的優(yōu)勢(shì)在于所用的樣本數(shù)和實(shí)驗(yàn)時(shí)間大大減少(濾波器收斂退出即可結(jié)束),非常適用于需要快速對(duì)陀螺儀隨機(jī)噪聲建模的場(chǎng)合。
2.4 基于魯棒Kalman濾波的AR模型在線實(shí)時(shí)建模
在某些需要極高精度或陀螺隨機(jī)噪聲特性強(qiáng)時(shí)變的場(chǎng)合,由外界環(huán)境等因素造成的陀螺儀隨機(jī)噪聲的時(shí)變性必須被考慮,這時(shí)傳統(tǒng)固定參數(shù)式的建模方法已不能適用。而Kalman濾波器可以利用新的陀螺噪聲觀測(cè)數(shù)據(jù)對(duì)系統(tǒng)狀態(tài)量,即AR模型的參數(shù)估計(jì)進(jìn)行修正,使建立的AR模型參數(shù)能及時(shí)地跟蹤陀螺隨機(jī)噪聲隨時(shí)間的變化,從而獲得更高的建模精度(但需注意在這種情況下Kalman濾波器的迭代退出時(shí)間只取決于需要建立的時(shí)變模型的時(shí)間長(zhǎng)短,建模的優(yōu)勢(shì)體現(xiàn)在精度而非速度上)。
例如,對(duì)該陀螺的噪聲數(shù)據(jù)分別采用新的基于魯棒Kalman的AR在線實(shí)時(shí)建模方法和傳統(tǒng)固定參數(shù)式Y(jié)-W法進(jìn)行建模。并采用殘差序列白化度檢驗(yàn)法[9]對(duì)兩種方法建模的結(jié)果進(jìn)行檢驗(yàn)。兩種方法建模過(guò)程中得到的殘差序列ε1(k)、ε2(k)的自相關(guān)函數(shù)如圖4所示。可以看出,基于魯棒Kalman的AR在線實(shí)時(shí)建模結(jié)果的殘差序列ε1(k)比傳統(tǒng)固定參數(shù)式

圖4 兩種AR建模方法對(duì)比
Y-W法的建模結(jié)果中的殘差序列ε2(k)白化程度更好,更接近白噪聲。因此說(shuō)明建模的精度優(yōu)于后者。
3 結(jié)束語(yǔ)
針對(duì)傳統(tǒng)的陀螺隨機(jī)噪聲AR建模方法收斂速度慢、所需樣本較多的缺點(diǎn),本文提出了基于魯棒Kalman濾波的AR模型建模方法。該方法將AR模型參數(shù)作為系統(tǒng)的狀態(tài)量,采用帶遺忘因子的噪聲統(tǒng)計(jì)估值器估計(jì)系統(tǒng)觀測(cè)噪聲的均值和方差。通過(guò)Kalman濾波迭代快速經(jīng)濟(jì)的估計(jì)出樣本的AR模型參數(shù),減少了采樣次數(shù)和實(shí)驗(yàn)時(shí)間。還能利用新的隨機(jī)噪聲信息實(shí)時(shí)修正AR模型參數(shù),使參數(shù)估值能及時(shí)地反映和跟隨陀螺儀隨機(jī)噪聲特性的變化,適用于要求快速建模或陀螺隨機(jī)噪聲具有強(qiáng)時(shí)變特性的工程場(chǎng)合。
[1]張慶,談?wù)穹F福,等.一種光纖陀螺隨機(jī)漂移的非平穩(wěn)時(shí)序建模法[J].傳感器與微系統(tǒng),2010,29(7):43-46.
[2]張秋昭,張書畢,侯東陽(yáng).光纖陀螺隨機(jī)漂移辨識(shí)方法研究[J].傳感器與微系統(tǒng),2011,30(9):50-56.
[3]李家壘,許化龍,何婧.光纖陀螺隨機(jī)漂移的實(shí)時(shí)濾波方法研究[J].宇航學(xué)報(bào),2010,31(12):2717-2721.
[4]陳俊杰,楊孟興.光纖陀螺隨機(jī)漂移時(shí)間序列建模研究[J].彈箭與制導(dǎo)學(xué)報(bào),2011,31(5):65-67.
[5]蒙濤,王昊,李輝,等.MEMS陀螺誤差建模與濾波方法[J].系統(tǒng)工程與電子技術(shù),2009,31(8):1944-1947.
[6]嚴(yán)恭敏,李四海,秦永元.慣性儀器測(cè)試與數(shù)據(jù)分析[M].北京:國(guó)防工業(yè)出版社,2012:135-150.
[7]DrostF C,AkkerR V D,WerkerB J M.Efficient estimation of auto-regression parameters and innovation distributions for semip-arametric integer-valuedAR(p)models[J].Journal of the Royal Statistical Society:Series B(Statistical Methodology),2009,71(2):467-485.
[8]Piet D J,Jeremy P.The ARMA model in state space form[J].Statistic&Probability Letters,2004,70(8):119-125.
[9]李言俊,張科.系統(tǒng)辨識(shí)理論及應(yīng)用[M].北京:國(guó)防工業(yè)出版社,2009:43-105.
Rapid/real-time AR modeling method for gyro random noise based on robust Kalman filter
HUANG Lei,ZHAO Ya-qin
(Mechanic and Electronic Engineering College,Nanjing Forestry University,Nanjing 210037,China)
To solve the problem of the traditional AR modeling methods for gyro random noise which need a large number of samples and can’t reflect the time-varying characteristic of the random noise timely,a new AR modeling method based on adaptive robust Kalman filter is developed.The AR model parameters are chosen to be the state variable.Unknown time-varying estimator of observation noise is used to achieve the estimates of the mean and variance of the observation noise.The AR model parameters can be estimated accurately by Kalman filter.Test results indicate that the new modeling method has the advantages of fast convergence and lowcost.When the new random noise samples are achieved,the Kalman filter can correct the model parameters timely.So the modeled AR parameters have high accuracy.The new modeling method can be applied to applications which need a rapid modeling or in which the gyro random noise has strong time-varying characteristic.
strapdown inertial navigation system;gyro random noise modeling;robust Kalman filter;time series
V241.5;TB535+.2;TN713;TN957.54
:A
:1674-5124(2014)06-0088-03
10.11857/j.issn.1674-5124.2014.06.023
2014-01-06;
:2014-03-01
國(guó)家自然科學(xué)基金項(xiàng)目(31200496)
黃 磊(1975-),男,安徽合肥市人,講師,博士,研究方向?yàn)榻萋?lián)慣性導(dǎo)航和嵌入式系統(tǒng)。

