一種基于多普勒頻率變化率單站無源定位的改進跟蹤濾波算法

談欣榮，高憲軍，李寶珠，王 宇

（1.空軍航空大學 研究生隊，吉林 長春 130022；2.空軍航空大學 科研部，吉林 長春 130022；3.空軍航空大學 軍事仿真技術研究所，吉林 長春 130022）

無源定位技術是一種定位設備本身并不主動發射信號，而僅僅依靠被動接收輻射源的信息來實現定位的技術[1]。單站無源定位主要有兩個方面的難點：一是相對較少的測量信息使得單一時刻的測量信息無法實現對目標輻射源的相對定位；二是目標輻射源復雜的運動形式使得精確的跟蹤方程難以建立，從而影響跟蹤算法的精度。針對上述困難，本文選擇了基于多普勒頻率變化率的無源定位方法進行定位。但是光靠單站無源定位技術還不足以獲取運動目標連續的位置信息，需要進行有效的跟蹤濾波。

在機動目標跟蹤領域，交互式多模型（IMM）算法[2-3]被認為是迄今為止最有效的算法之一。交互式多模型算法考慮了模型的特點，它假設目標有多種運動狀態，每一種運動狀態對應一種模型，目標在任意時刻的運動狀態都可以用給定模型中的一種來表示，而運動狀態的變化也就是運動模型之間的切換用齊次馬爾可夫鏈表示，目標的濾波結果是多個模型濾波結果的加權綜合。對于不同的應用要求，IMM算法又可能結合多種濾波算法。將IMM算法與卡爾曼濾波器（Kalman Filter，KF）或者無跡卡爾曼濾波器（Unscented Kalman Filter，UKF）結合，這樣做有算法簡單，計算量小等優點，但是這些算法存在線性化誤差，估計精度不高，且不適用于非高斯問題。將IMM算法與粒子濾波相結合的IMM-PF算法（Interacting Multiple Model Particle Filter）[4-9]集成了IMM對機動目標的跟蹤的良好特性，同時避免了線性化誤差和高斯噪聲的限制，有效的提高了狀態估計的精確度。但粒子濾波的主要問題是計算量大，若多模型中的每個模型匹配一個粒子濾波器，計算量無疑會很大，影響跟蹤的實時性。

針對以上問題，本文提出了一種改進的IMM濾波算法（IMMKF-UKF-PF）進行定位跟蹤。其原理是：將系統的多模型分成三類，一類是線性模型，匹配卡爾曼濾波；一類是三階及三階以下非線性高斯模型，匹配無跡卡爾曼濾波；一類是三階以上非線性高斯模型或非高斯模型，匹配粒子濾波。仿真結果表明該算法大大改善了計算效率。

1 利用多普勒頻率變化率的二維單站無源定位原理

如圖 1 所示，觀測平臺在位置（xo，yo）處以（x˙o，y˙o）作直線運動，目標輻射源在位置（xT，yT）處以（x˙T，y˙T）作直線運動，二者之間的相對位置（x，y）=（xT-xO，yT-yO）。

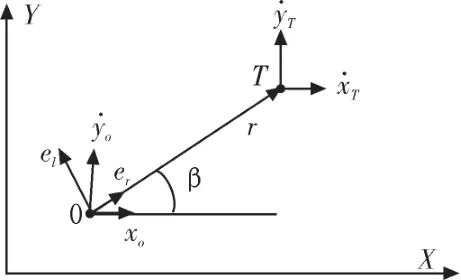
圖1 二維平面觀測平臺與目標輻射源幾何示意圖Fig.1 Observation platform and target in the two-dimensional

根據幾何關系和運動學原理，經過一系列推導得觀測站平臺和輻射源之間的距離為

然后根據三角原理得出目標輻射源的位置（xT，yT）:

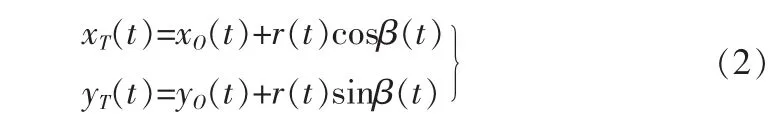
在多次測量的情況下，選擇適當的非線性跟蹤濾波算法，對輻射源進行跟蹤定位。

2 IMMKF-UKF-PF濾波算法

設一個使用確定模型集合 M={Mi|i=1，2，…，M}的混合系統，狀態方程和觀測方程離散形式為：

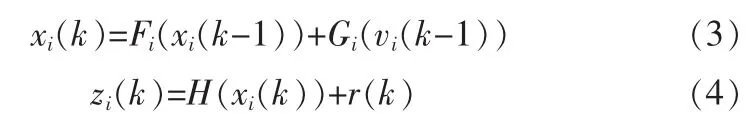
其中 xi（k）表示在模型 i（i=1，2，…，M）下的目標運動狀態矢量，vi是相應的非高斯過程噪聲，zi（k）是觀測矢量，r是高斯觀測噪聲。Qi（k）和 R 分別是 vi（k）和 r（k）的協方差。一共有 M 個模型，假設其中1到M1是線性的，M1到M2時是三階及三階以下非線性高斯模型，其它是三階以上非線性高斯模型或非高斯模型。

系統模型之間的轉移概率用一個馬爾可夫鏈來表示：

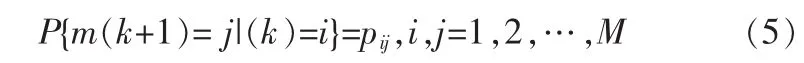
圖2給出了IMMKF-UKF-PF濾波算法結構示意圖，從k-1時刻開始到k時刻，一個采樣周期的IMMK-UKF-PF實現步驟如下：

步驟1：輸入交互

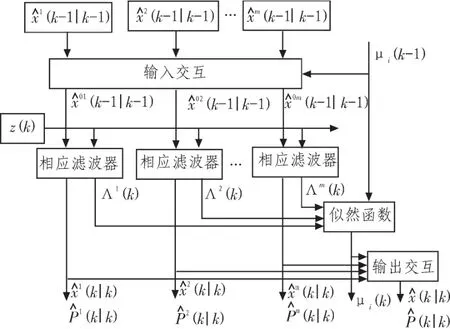
圖2 IMMKF-UKF-PF濾波算法結構示意圖Fig.2 Filter algorithm structure of IMMKF-UKF-PF

步驟2：濾波

在交互運算的結果和觀測量z（k）的基礎上，通過 3種濾波器，得到各模型的狀態估計量x?i（k|k）和協方差估計量P?i（k|k）。由于進行濾波算法時與常規的IMM-KF、IMM-UKF算法和IMM-PF算法近似，這里不再贅述。

步驟3：模型概率更新

各模型概率更新如下：

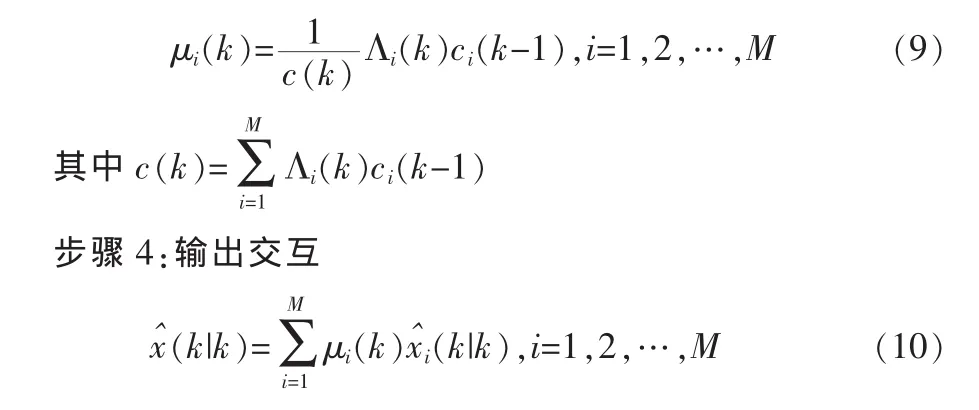
3 數學建模及仿真驗證

為了驗證本文改進的IMM算法的有效性，將其與IMM-UKF、IMM-PF算法進行Matlab仿真，并將仿真結果進行比較分析。

仿真中采用CV模型、CA模型和JERK模型[10]進行交互。

當目標處于勻速運動時，用xi=xTi-xOi、yi=yTi-yOi表示目標的相對位置，用表示目標與觀測站相對速度，選取狀態變量建立如下狀態方程：

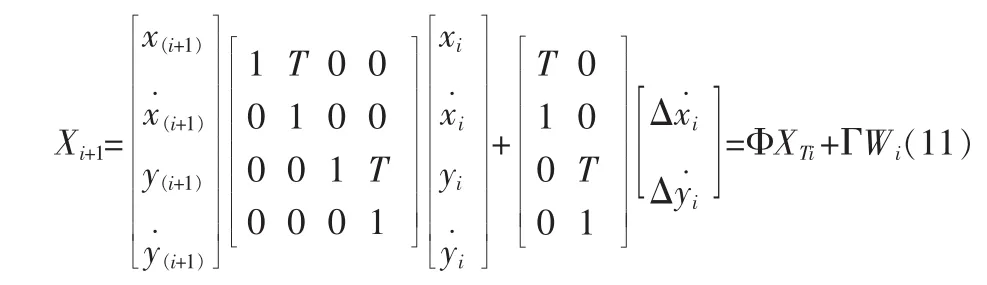
建立如下狀態方程：

當目標處于變加速運動時：X或Y一維情況下狀態轉移矩陣為

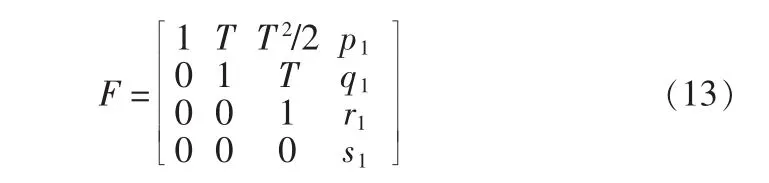
式 中 p1=（2-2αT+α2T2-2e-αT）/2a3，q1=（e-αT-1+αT）/α2，r1=（1-e-αT）/α，s1=e-αT，參數 α 為“機動”頻率。

觀測方程

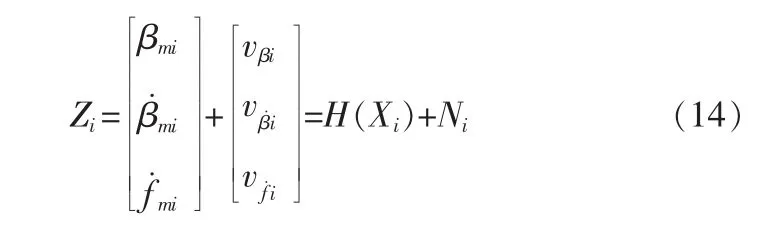
下標 m 表示為含有噪聲的觀測量， 其中 vβ、vβ˙、 vf˙分別為相互獨立服從零均值高斯分布的測量誤差。

假設測量條件為：觀察間隔為T=1 s，波達角、波達角變化率和頻率變化率的測量精度分別取：5×10-3rad、0.2×10-3rad/s、1 Hz/s。各模型濾波狀態初始化，假定目標距離搜索范圍為0～500 km，目標速度范圍假定為-500～500m/s，且初始分布假定為均勻分布，在此假定下可由概率論知識得到目標位置和速度的期望值以及相應協方差值。 X（0）=[8 000，50，7 000，60]T是初始狀態矢量，P=diag（1，1，1，1）是初始狀態協方差，各模型初始概率均為1/3，模型轉移概率矩陣為

粒子濾波時模型的粒子數為N=800，蒙特卡羅仿真次數為100。

仿真結果如圖3、4、5所示，分別表示IMM-UKF、IMMPF、IMMKF-UKF-PF 3種算法估計目標位置的誤差曲線。

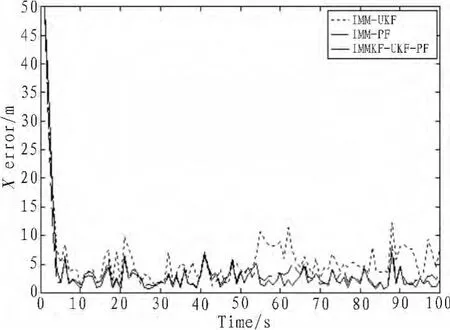
圖3 X方向均方根誤差Fig.3 Error of X direction

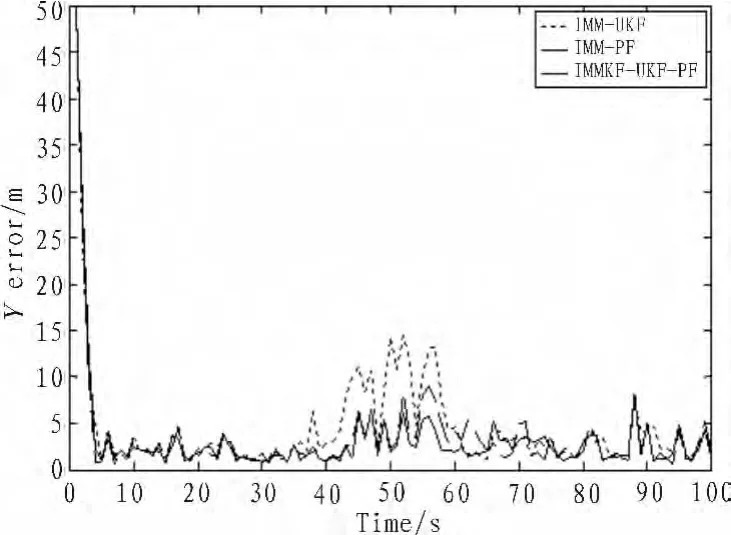
圖4 Y方向均方根誤差Fig.4 Error of Y direction

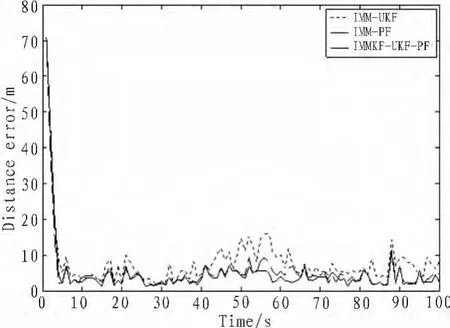
圖5 R方向均方根誤差Fig.5 Error of R direction

Execution time （seconds）

TIMM-UKF=5.451 2，TIMM-PF=13.451 2，TIMMKF-UKF-PF=6.032 4

由圖3、4、5以及仿真時間可以得出，IMMKF-UKF-PF濾波算法的均方根誤差略小于IMM-PF算法，跟蹤性能有一定的改善，IMM-UKF算法跟蹤性能最不理想；最重要的是IMMKF-UKF-PF濾波算法仿真所用時間相比IMM-PF減少很多，與IMM-UKF相近，這在現實應用中具有重要的意義。

4 結束語

本文在基于多普勒頻率變化率的單站無源定位問題的基礎上提出了一種改進的交互式多模型濾波算法 （IMMKFUKF-PF），利用不同的模型匹配不同類型的濾波器，IMMKFUKF-PF算法充分發揮了粒子濾波和無跡卡爾曼濾波以及卡爾曼濾波各自的優點，大大地提高了計算效率，減少了跟蹤定位所用時間，同時該算法具有良好的跟蹤性能和較強的魯棒性。在實際的機動目標跟蹤中，目標的運動情況比較復雜，往往需要多個不同參數的線性及非線性模型進行匹配，在這種情況下，采用IMMKF-UKF-PF算法改善的計算負荷是可觀的。

[1]華鐵洲.單站無源定位關鍵技術研究和誤差分析[D].河南:信息工程大學信息工程學院，2010.

[2]楊麗娜，袁鑄.CS模型下的IMM算法在目標跟蹤中的應用[J].計算機工程與應用，2010，46（33）:230-232.YANG Li-na，YUAN Zhu.Application of IMM algorithm based onmodelCS in target tracking[J].Computer Engineering and Applications，2010，46（33）:230-232.

[3]宮淑麗，王幫峰，吳紅蘭，等.基于IMM算法的機場場面運動目標跟蹤[J].系統工程與電子技術，2011，33（10）:2322-2326.GONG Shu-li，WANG Bang-feng，WU Hong-lan.Tracking of moving targets on airport surface based on IMM algorithm[J].SystemsEngineeringand Electronics，2011，33（10）:2322-2326.

[4]劉長江，王超鋒，宋春林.基于時差及多普勒頻差的IMM無源定位算法[J].現代雷達，2011，33（5）:36-38.LIU Chang-jiang，WANG Chao-feng，SONG Chun-lin.IMM algorithm for passive location based on TDOA and FDOA[J].Modern Radar，2011，33（5）:36-38.

[5]華鐵洲，李冬海，陳劍宇.一種改進的單站無源定位算法[J].電子對抗，2010（2）:11-14.HUA Tie-zhou，LI Dong-hai，CHEN Jian-yu.An improved single observer passive location algorithm[J].Electronic Countermeasures，2010（2）:11-14.

[6]王喜鵬，王飛.機載無源定位精度分析[J].艦船電子對抗，2012，35（3）:24-26.WANG Xi-peng，WANG Fei.Analysis of airborne passive location precision[J].Shipboard Electronic Countermeasure，2012，35（3）:24-26.

[7]楊曉君，陸芳.模糊單站無源定位方法[J].清華大學學報，2011，51（1）:25-29.YANG Xiao-jun，LU Fang.Obscure method of single observer passive location[J].Journal of Tsinghua University，2011，51（1）:25-29.

[8]Boers Y，Driessen J N.Interacting multiple model particle filter[J].IEE Proc.-Radar Sonar Navig，2003，150（5）:344-349.

[9]BLOM H A P，Bloem E A.Particle Filtering for Stochastic Hybrid Systems[C]//43 IEEE Conference on Decision and Control，2004.USA:IEEE，2004，3:3221-3226.

[10]楊翠芳，汪圣利，周豐.基于參數自適應Jerk模型的IMMUKF算法[J].自動化技術與應用，2010，29（1）:47-52.YANG Cui-fang，WANG Sheng-li，ZHOU Feng.Interacting multipie model UKF algorithm based on jerk model with adaptive parameter[J].Techniques of Automation and Applications，2010，29（1）:47-52.